4.5 Погрешность метода трапеций

Абсолютная погрешность метода трапеций при равномерном шаге интегрирования есть величина

.

Она складывается из погрешностей , получаемых на частичных отрезках интегрирования,

,

где

, .

Оценка погрешности определяется выражением

.

Чтобы оценить , рассмотрим функцию

, .

Очевидно, что , . Кроме того,

,

,

,

.

Обозначим

, .

Тогда

.

По этой причине

,

.

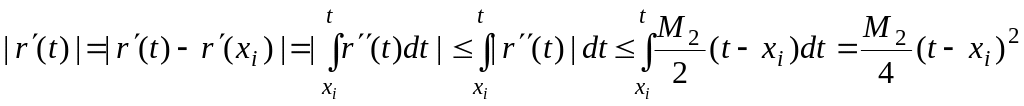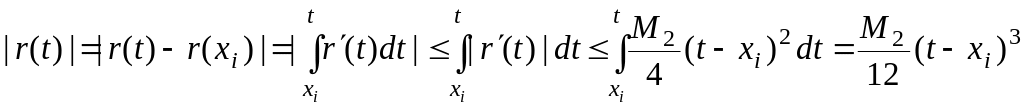Следовательно,

.

Оценка абсолютной погрешности на всем отрезке интегрирования определяется выражением

,

где – максимальное по модулю значение второй производной подынтегральной функции на отрезке интегрирования . Мы видим, что погрешность метода прямоугольников имеет тот же порядок, что и . Поскольку для функций вида имеем , , то для таких функций (для полиномов первой степени) формула трапеций является точной.

4.6 Метод Симпсона

В основе метода Симпсона лежит следующая лемма.

Лемма. Если или , то

. (4.5)

Выполним доказательство лишь для квадратичной параболы. Подставим функцию под интеграл в (4.5) и вычислим его. Получим

. (4.6)

С другой стороны,

,

,

.

Сложив три последних выражения, мы получим выражение (4.6), что и доказывает лемму.

Перейдем к изложению метода Симпсона. Разделим точки , разбивающие отрезок интегрирования на частичные отрезки с равномерным шагом , на тройки точек , ,…, . Для такого разбиения число отрезков необходимо выбрать четным. На отрезке, определяемом -й тройкой точек , , заменим подынтегральную функцию параболой второго порядка , проходящей через точки , , , и заменим точное значение интеграла на этом отрезке интегралом от полученной параболы. На основании леммы можно записать, что

.

Приближенное значение интеграла на всем отрезке интегрирования получим как сумму этих частичных интегралов:

. (4.7)

Мы видим, что в методе Симпсона крайние значения функции суммируются с весом 1, значения с нечетным номером – с весом , и значения с четным номером – с весом . Суммы значений функции с различными весами удобно вычислить отдельно, а затем их сложить, умножить на шаг и разделить на 3.

4.7 Погрешность метода Симпсона

Абсолютная погрешность формулы Симпсона (4.7) определяется выражением

.

Она складывается из частичных погрешностей , полученных на каждой тройке точек, используемых для аппроксимации:

.

Частичная погрешность здесь определяется выражением

.

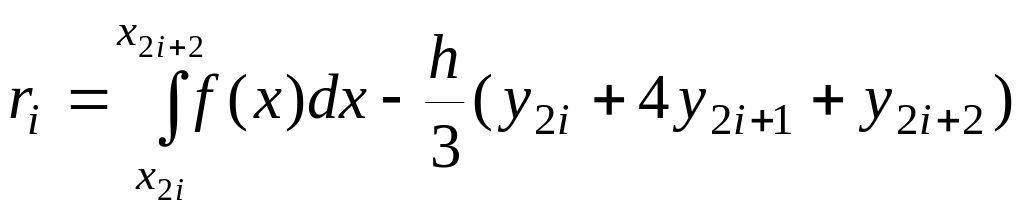Оценка общей погрешности имеет вид:

. (4.8)

Получим оценки сначала для частичной, а затем и для полной погрешностей. Для этого рассмотрим вспомогательную функцию

, .

При и эта функция совпадает с . Кроме того, . Найдем производные функции до 3-го порядка включительно. Поскольку

,

то, используя правила дифференцирования интеграла по нижнему и верхнему пределам, получим

,

а также

,

.

Выполняя последовательное дифференцирование, будем иметь

,

,

,

.

Применяя к теорему Лагранжа, т.е. используя равенство

, ,

получим

.

Обозначая максимальное по модулю значение четвертой производной подынтегральной функции на отрезке интегрирования ,

,

получим оценку для 3-й производной функции :

.

Поскольку

,

то

.

Аналогично получаем

,

,

,

.

Поскольку , то для частичной погрешности получаем оценку

.

Выражение (4.8) имеет слагаемых, следовательно, абсолютная погрешность формулы Симпсона будет оцениваться выражением

.

Из последней формулы видно, что абсолютная погрешность метода Симпсона имеет тот же порядок, что и . Формула Симпсона точна для полиномов третьей степени, поскольку для полинома 3-й степени . Это является следствием того, что лемма (4.5) справедлива также для полинома 3-й степени.