2.7. Приклад 1.

Знаходження рівняння парної регресії.

Приклад 1. За даними вибіркового дослідження відомі значення двох показників: – середньоденна заробітна плата одного працюючого, Y – витрати на придбання продовольчих товарів в відсотковому відношенні до загальних витрат.

Таблиця 2.2

, грн.	45	60	57	62	59	47	55
, %	69	61	60	57	55	67	65

Побудувати лінійну модель залежності від . Розрахувати коефіцієнти кореляції, детермінації. Оцінити модель через середню похибку апроксимації та -критерій Фішера, зробити прогноз для індивідуальних значень при грн.

Розв’язання.

Для розрахунку параметрів лінійної регресії розв’язуємо систему нормальних рівнянь (див. 2.1.2)

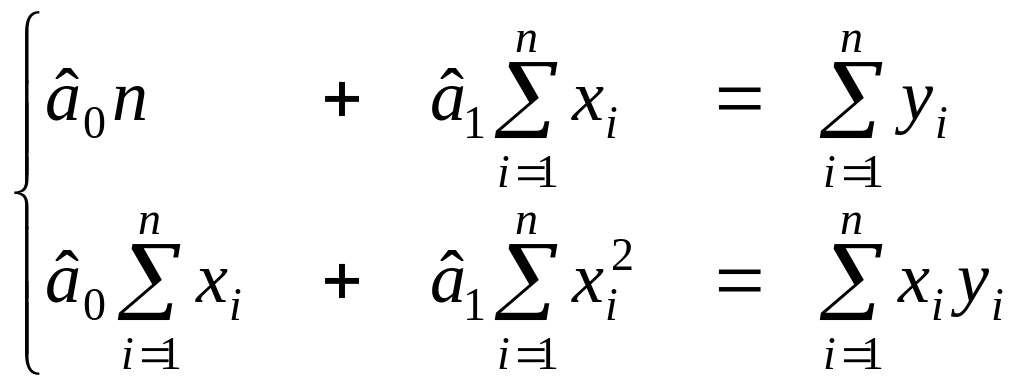
За вихідними даними розраховуємо , , , , . Ці розрахунки можна проводити використовуючи розрахункову таблицю 2.3.

Таблиця 2.3

1	69	45	3105	2025	4761	69,05	-0,05	0,08
2	61	60	3660	3600	3721	58,47	2,5	4,14
3	60	57	3420	3249	3600	60,59	-0,59	0,98
4	57	62	3534	3844	3249	57,06	-0,06	0,11
5	55	59	3245	3481	3025	59,18	-4,18	7,60
6	67	47	3149	2209	4489	67,64	-0,64	0,96
7	65	55	3575	4225	4225	62	3	4,62
Разом,	434	385	23688	21433	27070	434		18,48
Середні значення	62	58	3384	3061,86	3867,14			2,64
	23,14	36,87
	4,81	6,07

В останньому стовпчику таблиці записано значення величини .

За формулами (1.3.5), (1.3.6) знаходимо:

, .

Рівняння регресії має вигляд:

.

Із збільшенням середньої заробітної плати на 1 грн. частка витрат на придбання продовольчих товарів знижується в середньому на 0,71%.

Розрахуємо лінійний коефіцієнт парної кореляції за формулою (1.4.1)

.

Зв’язок обернений, тісний.

Визначаємо коефіцієнт детермінації за формулою (1.5.1)

.

Варіація (дисперсія) результативної ознаки на 0,89% пояснюється варіацією фактора .

Підставляючи в рівняння регресії фактичні значення визначаємо теоретичні (розрахункові) значення . Знаходимо величину середньої похибки апроксимації

%.

В середньому розрахункові значення відхиляються від фактичних на 2,64%, що знаходиться в допустимих межах.

Оцінимо значущість рівняння регресії за допомогою -критерію Фішера. Знайдемо фактичне значення . Для цього в розрахунковій таблиці можна додатково внести колонки і . Тоді

.

Так як , то отримане рівняння є статистично значущим.

Знайдемо прогнозні значення для індивідуальних значень при грн. Для цього заповнимо допоміжну розрахункову таблицю 2.4.

Таблиця 2.4

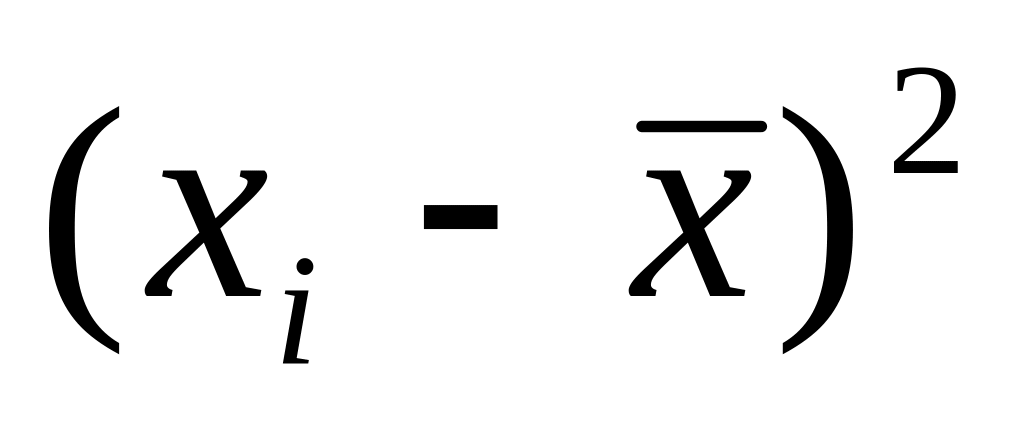
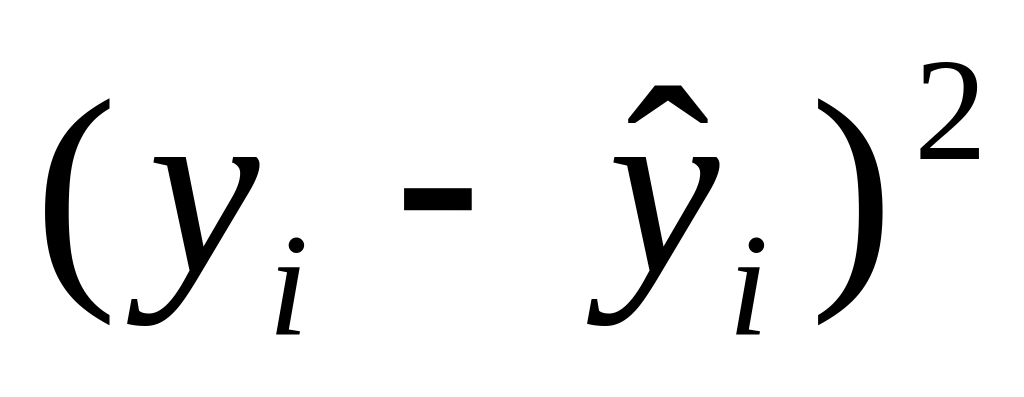
1	69	45	100	69,05	0,00
2	61	60	25	58,47	6,39
3	60	57	4	60,59	0,35
4	57	62	49	57,06	0,00
5	55	59	16	59,18	17,46
6	67	47	64	67,64	0,41
7	65	55	0	62	9,00
Разом,	434	385	258	434	33,61

Знаходимо точкове значення прогнозу:

.

Для лінійної моделі число параметрів , тому незміщена оцінка дисперсії залишків

, .

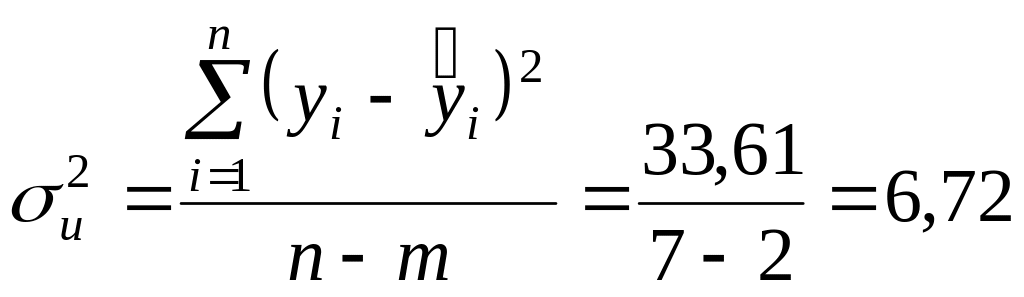Знаходимо дисперсію індивідуальних значень при

.

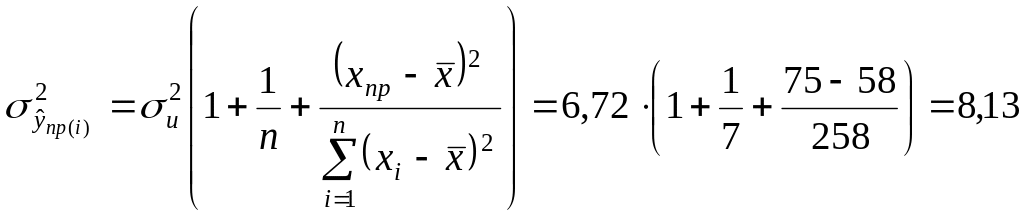За таблицями знаходимо

.

За формулою отримуємо:

.

Отже з ймовірністю 0,95 витрати на придбання продовольчих товарі будуть знаходитися в інтервалі

.