2.2. Властивості оцінок

Оцінки параметрів моделі повинні задовольняти умовам:

• обґрунтованості,

• незміщеності,

• ефективності.

Оцінка називається обґрунтованою, якщо для довільного, як завгодно малого числа виконується умова

.

Іншими словами, оцінка вважається обґрунтованою , якщо вона задовольняє закону великих чисел. Закон великих чисел у формі Чебишева стверджує, що вибіркове середнє є обґрунтованою оцінкою математичного сподівання генеральної сукупності. Так як оцінки виражаються через середні величини, які є обґрунтованими оцінками, то і є обґрунтованими оцінками.

Властивість незміщеності означає, що математичне сподівання оцінки параметра дорівнює значенню параметра :

.

Зміщення оцінки визначається так

.

Наявність зміщення або його відсутність може бути перевірена з допомогою відношення середнього квадратичного відхилення до абсолютної величини оцінки . Якщо

,

то роблять висновок про зміщеність оцінки.

Незміщена оцінка називається ефективною, якщо вона має найменшу дисперсію, серед всіх можливих незміщених оцінок параметра , обчислених на основі вибірок однакового обсягу .

Для 1МНК оцінок справедлива теорема Гаусса – Маркова: при виконанні передумов до застосування 1МНК, оцінки 1МНК є найбільш ефективними, тобто мають найменшу дисперсію в класі лінійних незміщених оцінок (Best Linear Unbiased Estimator або BLUE). Доведення теореми буде розглянуто пізніше.

Іноді окремо виділяють четверту властивість оцінок - інваріантність. Оцінки параметрів називаються інваріантними, якщо оцінкою довільної функції буде функція . Ця властивість дає можливість, знаючи одні оцінки параметрів, знаходити інші, якщо останні виражаються через перші.

2.3. Лінійний коефіцієнт кореляції

Лінійний коефіцієнт кореляції характеризує тісноту і напрям лінійного зв’язку між змінними і .

Лінійний коефіцієнт кореляції може обчислюватися за формулами

; (2.3.1)

; (2.3.2)

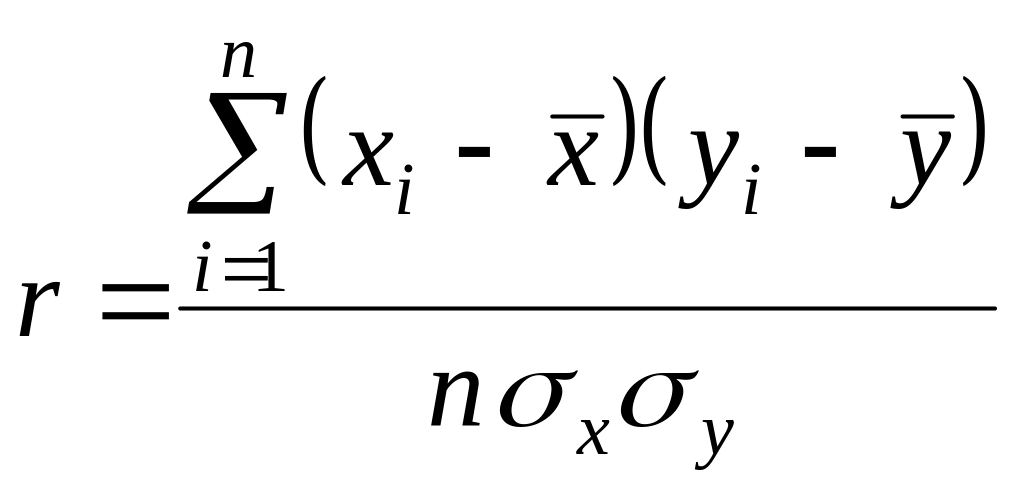; (2.3.3)

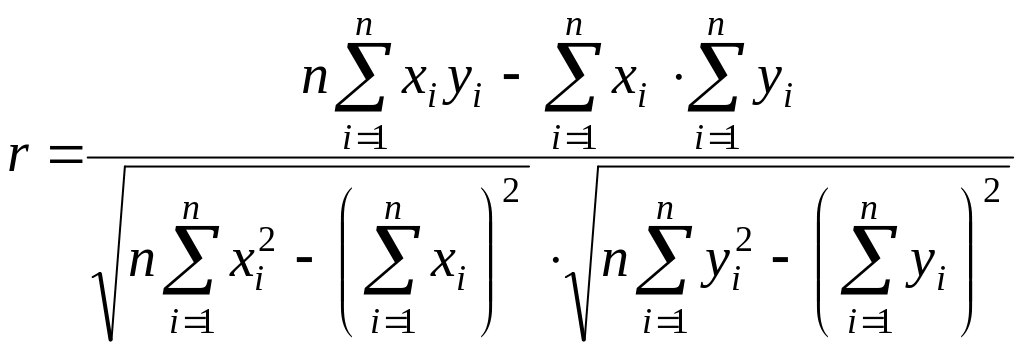, (2.3.4)

де – вибіркові середні квадратичні відхилення відповідно і .

Властивості коефіцієнта кореляції

1о	Коефіцієнт приймає значення на відрізку , тобто . Чим ближче до 1, тим тісніший зв’язок.
2о	Якщо , то зв’язок прямий, якщо – зв’язок обернений. При прямому (оберненому) зв’язку збільшення пояснювальної змінної веде до збільшення (зменшення) залежної змінної.
3о	При зв’язок між і функціональний.
4о	При лінійний зв’язок між і відсутній.

Поряд з коефіцієнтом кореляції, одним із показників, що характеризують кількісний зв’язок між залежною і незалежною змінними є коефіцієнт еластичності. Для лінійної парної регресійної моделі даний коефіцієнт розраховується за формулою

. (2.3.5)

Він показує, на скільки відсотків в середньому зміниться залежна змінна при зміні незалежної змінної в середньому на один відсоток при інших незмінних умовах.

Якщо модель є нелінійною, то для характеристики еластичності зв’язку розраховують середній коефіцієнт еластичності або коефіцієнт еластичності для певної точки . Середній коефіцієнт еластичності показує, на скільки відсотків у середньому по сукупності зміниться результат від своєї середньої величини при зміні фактору х на 1% від свого середнього значення:

, (2.3.6)

де – перша похідна при .

Коефіцієнт еластичності для певної точки обчислюється за формулою

. (2.3.7)