4.3. Приклад 4.

Перевірка на наявність мультиколінеарності

за алгоритмом Фаррара – Глобера

Приклад 4. Відомо, що на середньомісячну заробітну плату , впливають три фактори: рівень рентабельності – , витрати капіталу - , фондовіддача - . Необхідні дані наведено в таблиці .

, %	10,7	11,0	12,2	12,4	10,9	11,3	11,1
, ум. од.	38	29	30	25	24	31	30
, ум. од.	39	33	38	31	29	37	36
, ум. од.	63	70	80	84	69	72	70

Перевірити фактори , , на наявність мультиколінеарності за допомогою алгоритму Фаррара – Глобера.

Розв’язання.

Кроки 1-2-й. Для зручності числових обчислень об’єднаємо кроки перший і другий в один і розраховуємо кореляційну матрицю . Ця матриця симетрична. В нашому випадку розмір матриці . Матриця має вигляд:

,

де елементи матриці розраховуються за формулами:

,

, ,

,

.

Для розрахунку сформуємо допоміжну розрахункову таблицю 4.1.

Таблиця. 4.1

№
1	10,7	38	39	114,49	1444	1521	406,6	417,3	1482
2	11,0	30	33	121	900	1089	330	363	630
3	12,2	30	38	148,84	900	1444	336	463,6	1140
4	12,4	25	31	153,76	625	961	310	384,4	775
5	10,9	24	29	118,81	576	841	261,6	316,1	696
6	11,3	30	37	127,69	900	1369	339	418,1	1110
7	11,1	30	36	123,21	900	1296	333	399,6	1080
Середні значення	11,37	29,57	34,71	129,69	892,43	1217,29	335,21	394,59	1039,57
	0,38	17,96	12,20
	0,61	4,24	3,49

Тоді

,

аналогічно

, .

Кореляційна матриця має вигляд:

.

Елементами матриці є коефіцієнти парної кореляції незалежних змінних. В нашому випадку , , . Отже, як бачимо між парами незалежних змінних існує зв’язок різної тісноти.

Крок 3-й. Знаходимо визначник матриці

.

Крок 4-й. Обчислюємо статистику за формулою

.

В нашому випадку число спостережень , число пояснюючих змінних тому

.

При рівні значущості і числі ступенів свободи за таблицею знаходимо критичне значення

.

Так, як , то мультиколінеарність в масиві незалежних змінних присутня. Якби виявилось, що , то це б означало, що мультиколінеарність відсутня, тобто нею можна знехтувати, і дальші дослідження за алгоритмом можна не проводити.

Крок 5-й. Знайдемо обернену матрицю до матриці за допомогою формули:

,

де алгебраїчне доповнення до елементу матриці

.

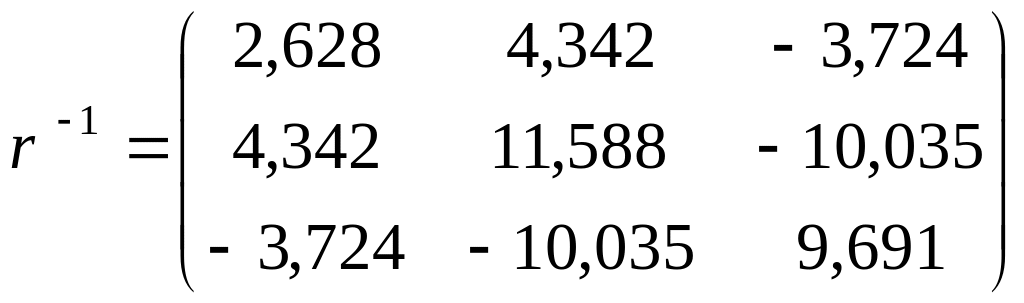Крок 6-й. Розраховуємо - критерій за формулою де діагональні елементи матриці . Таким чином отримуємо стільки фактичних значень скільки є пояснюючих змінних, тобто три: ,

Отримані фактичні значення статистики порівнюються з табличними для ступенів свободи знаменника, ступенів свободи чисельника і рівня значущості . В нашому випадку за таблицями . Так як , то змінна не корелює з масивом і . Так як і , то корелює з масивом змінних і , а корелює з масивом змінних і .

Крок 7-й. Обчислюємо частинні коефіцієнти кореляції

,

де , , – елементи матриці .

В нашому випадку отримаємо:

,

,

.

Як бачимо між факторами і зв’язок найтісніший. Частинні коефіцієнти кореляції характеризують кореляцію між змінними і за умови, що інші змінні на зв’язок не впливають.

Крок 8-й. Розраховуємо - статистику

,

,

,

.

Модулі отриманих фактичних значень - статистики порівнюємо з табличним , яке знаходиться для числа ступенів свободи і рівня значущості . В нашому випадку Так як , то між змінними і існує взаємозалежність. Взаємозв’язку між змінними і , а також між змінними і нема, так як , і .

Один із можливих методів усунення мультиколінеарності – це виключення однієї із змінних з моделі. Із економічних міркувань в нашому випадку при дослідженні залежності рівня заробітної плати від факторів краще виключити із розгляду фактор – фондовіддача і залишити фактор – затрати капіталу.

Після виключення цієї змінної повторимо перевірку на мультиколінеарність серед масиву змінних, що залишилися.

Кроки 1-2-й. Так як залишилися змінні, то кореляційна матриця матиму вигляд

Крок 3-й. Знаходимо детермінант матриці

.

Крок 4-й. Обчислюємо статистику формулою

.

В нашому випадку число спостережень , число пояснюючих змінних , тому

.

Так, як , то мультиколінеарність в масиві незалежних змінних відсутня або, ще кажуть, знаходиться в допустимих межах.

4.4. Методи усунення мультиколінеарності.

Різні методи, які можуть бути використані для зменшення негативних наслідків мультиколінеарності, умовно класифікують на дві категорії: прямі способи покращити умови надійності регресійних оцінок і непрямі способи.

Прямі способи базуються на наступних міркуваннях і відповідних їм діях.

По-перше, дисперсії оцінок параметрів пропорційні залишковій дисперсії . Випадковий член відображає вплив на змінну всіх регресорів (пояснюючих змінних), які не включені в модель. Отже, якщо можна знайти важливу, з економічних міркувань, змінну і включити її в модель, то таким чином ми зменшимо і покращимо надійність оцінок. Разом з тим, нова чи нові змінні можуть бути зв'язані лінійною залежністю із змінними, які вже включені в модель, і, таким чином ми можемо, навіть, підсилити проблему мультиколінеарності.

По-друге, дисперсії оцінок параметрів обернено-пропорційні величині вибірки (числу спостережень) . Значить, збільшивши кількість спостережень, ми автоматично зменшимо дисперсії оцінок параметрів і покращимо їх надійність.

Якщо вивченню підлягають часові ряди, то збільшити обсяг вибірки можна, якщо використовувати квартальні дані замість річних. Разом з тим, треба мати на увазі, що таким чином ми можемо внести або підсилити автокореляцію даних, по-друге в цьому підході ми можемо внести або підсилити зміщення оцінок параметрів, викликане похибками вимірювання.

По-третє, так як дисперсії оцінок параметрів , обернено пропорційні дисперсії пояснювальних змінних , то дані необхідно підбирати таким чином, щоб були найбільшими. Наприклад, якщо ми вивчаємо залежність товарообігу магазинів від величини торгової площі, то необхідно так сформувати вибірку, щоб там були і невеликі магазини з малою торговою площею і великі магазини.

По-четверте, при плануванні експерименту необхідно підбирати такі регресори, які були б якомога менше залежні один від одного.

Непрямі способи базуються на наступних міркуваннях і відповідних їм діях направлених на зменшення негативних наслідків мультиколінеарності.

По-перше, самий простий спосіб зменшення мультиколінеарності полягає в тому, щоб із двох пояснювальних змінних , які мають високий коефіцієнт кореляції і для яких одну виключити із розгляду. При цьому, яку змінну залишити, а яку виключити із аналізу, вирішують, в першу чергу, виходячи із економічних міркувань, тобто залишають в моделі більш важливу з економічної точки зору змінну. Якщо із економічних міркувань ні одній із них не можна надати перевагу, то залишають ту із змінних, яка має більший коефіцієнт кореляції із залежною змінною.

По-друге, якщо корельовані змінні зв'язані між собою концептуально, то можливо, краще об'єднати їх в один сукупний індекс.

По-третє, для зменшення мультиколінеарності можливий перехід від вихідних пояснювальних змінних між якими виявлена кореляція до нових змінних, які виражаються через лінійні комбінації вихідних. Нові змінні , які є лінійними комбінаціями змінних називаються головними компонентами. При цьому нові змінні підбираються таким чином, щоб вони не корелювали між собою, а потім знаходять рівняння зв'язку .