3. Багатофакторний регресійний аналіз
3.1. Класична нормальна лінійна модель
багатофакторної регресії
Багатофакторний регресійний аналіз є узагальненням парного регресійного аналізу на випадок, коли залежна змінна зв’язана більш ніж з однією пояснювальною змінною.
В багатофакторному регресійному аналізі в порівнянні з парним регресійним аналізом виникають, принаймні, дві нові проблеми. По-перше, необхідно вирішити проблему специфікації, так як залежна змінна залежить від багатьох змінних і необхідно вирішити, які з них є домінуючими і які необхідно включати в модель, а які ні.
По-друге, при аналізі впливу
конкретної пояснювальної змінної
на
необхідно відокремити вплив на
змінної
від впливу інших пояснювальних змінних.
Будемо вважати, що проблема специфікації вирішена і багатофакторна лінійна регресійна модель в загальному вигляді буде
.
Позначимо
-е
спостереження залежної змінної
,
а відповідні значення залежних змінних
.
Тоді лінійна модель матиме вигляд
,
(3.1.1)
Модель (3.1.1), в якій залежна
змінна
,
пояснюючі змінні
,…,
а також залишки
задовольняють умовам Гаусса-Маркова і
крім того, пояснювальні змінні
,…,
є незалежними, називається класичною
нормальною лінійною моделлю багатофакторної
регресії (Classic Normal Linear Multiple Regression Model).
В випадку багатофакторної регресії модель (3.1.1) зручно всі викладки проводити в матричному вигляді. Для цього введемо позначення
(3.1.2)
– матриця значень пояснюючої
змінної розміру
,
де
– кількість спостережень, а
– кількість параметрів моделі.
В матриці введено додатковий стовпчик із одиниць, чим враховується наявність в моделі вільного члена .
(3.1.3)
– матриця-стовпчик пояснювальної
змінної. Позначення
– означає транспонування.
(3.1.4)
– матриця-стовпчик параметрів моделі.
Тоді рівняння (3.1.1) запишеться так
.
(2.1.5)
Використовуючи ІМНК можна показати, що параметри моделі знаходяться з матричного рівняння (за допомогою оператора оцінювання)
,
(3.1.6)
де
транспонована матриця
,
– матриця обернена до
.
Останнє рівняння (оператор оцінювання) представляє собою матричну форму запису розв’язку системи нормальних рівнянь для знаходження параметрів моделі.
3.2. Коефіцієнти детермінації і кореляції.
Оцінка значущості багатофакторної регресії
Як і у випадку парної регресійної моделі, в моделі багатофакторної регресії загальна варіація (сума квадратів відхилень залежної змінної від середнього значення) може бути розкладена на дві складові
, (3.2.1)
де і – відповідно сума квадратів відхилень зумовлена регресією і залишкова сума квадратів, яка характеризує вплив на пояснювальну змінну всіх неврахованих чинників.
Значення варіацій
можуть бути обчислені за формулами
,
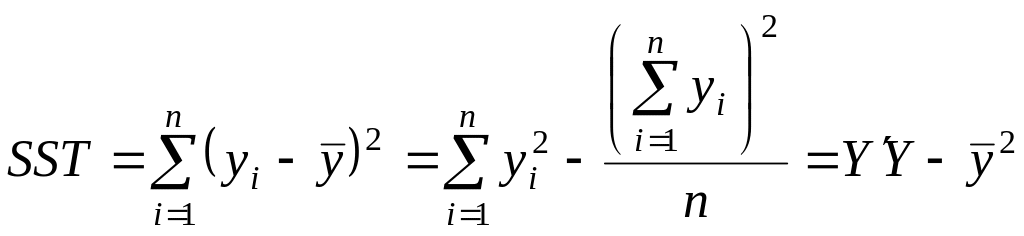(3.2.2)
,
(3.2.3)
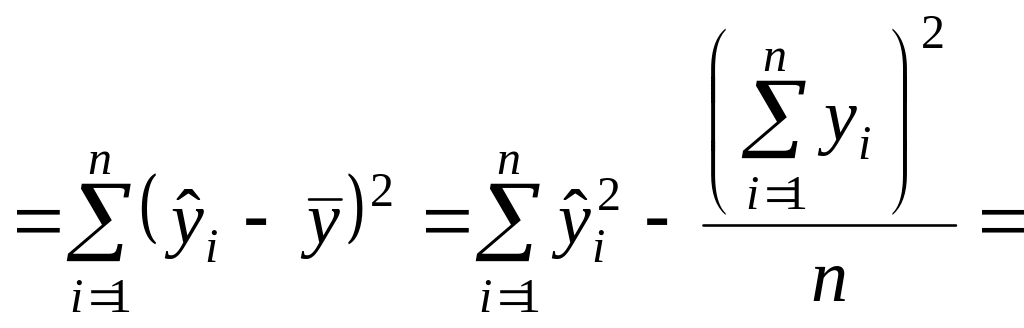
3.2.4)
Коефіцієнт детермінації дає одну з найбільш ефективних оцінок адекватності регресійної моделі. Він є мірою якості моделі і її прогностичної сили. Даний коефіцієнт показує, яка частина дисперсії пояснювальної змінної пояснюється регресією. Коефіцієнт детермінації знаходиться за формулою
,
(3.2.5)
або за формулою
,
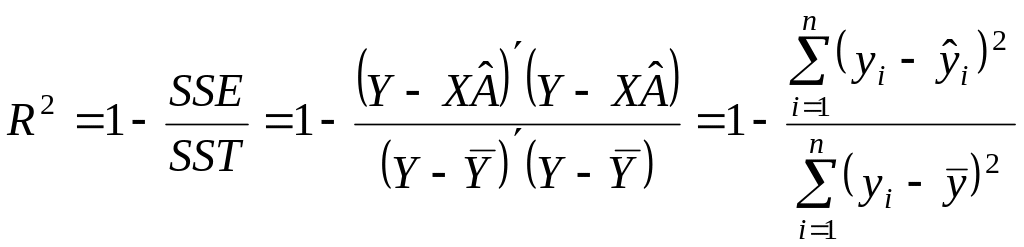(3.2.6)
або
.
(3.2.7)
Коефіцієнт детермінації
змінюється в межах
.
Чим ближче
до одиниці, тим краще регресія описує
залежність між пояснювальними і залежною
змінною.
Іноді обчислюють скоректований
(адаптований, нормований, виправлений)
коефіцієнт детермінації
,
який враховує число ступенів свободи
і обчислюється за формулою
.
(3.2.8)
Справді, так як для коефіцієнт детермінації знаходиться за формулою
,
тоді
,
або
,
звідки і отримується формула (3.2.8).
Коефіцієнт детермінації
,
обчислений без врахування числа ступенів
свободи буде збільшуватися при введені
в модель нових пояснювальних змінних,
хоча це і не завжди буде означати
покращення моделі. Скоректований
коефіцієнт детермінації
не має такого недоліку. Він може навіть
зменшуватися при введені в модель нових
пояснювальних змінних, якщо вони не
дають суттєвого покращення якості
моделі.
Зауважимо, що збільшення коефіцієнта детермінації не завжди означає покращення якості моделі. Велике значення коефіцієнта детермінації може бути наслідком того, що досліджувані показники мають часовий тренд.
Коефіцієнт багатофакторної
кореляції (або теоретичне
кореляційне співвідношення, індекс
кореляції
по
)
дорівнює квадратному кореню із коефіцієнту
детермінації, тобто
.
Для оцінки тісноти зв’язку між показниками, що входять до моделі розраховуються коефіцієнти парної кореляції. Розрахунок коефіцієнтів парної кореляції може бути проведено за формулами
;
.
Для характеристики зв’язку між ознаками розраховують також коефіцієнти еластичності. Для лінійної багатофакторної моделі вони розраховуються за формулою аналогічною як для парної лінійної регресії
.
Коефіцієнти еластичності в
даному випадку мають такий самий зміст,
як і для парної лінійної регресії:
показує, на скільки відсотків в середньому
зміниться залежна змінна при зміні
незалежної змінної
в середньому на один відсоток при інших
незмінних умовах.
Перевірка значущості моделі здійснюється за допомогою -критерію Фішера. Якщо коефіцієнт детермінації відомий, то - критерій Фішера розраховується за формулою
.
(3.2.9)
Отримане значення -критерію порівнюється з табличним для рівня значимості і числа ступенів свободи чисельника і - числа ступенів свободи знаменника. Якщо
,
то рівняння вважається статистично значущим.
Нагадаємо, що
– число спостережень,
– число пояснювальних змінних ,
– число параметрів моделі.