1.3.2. Неопределенность и неоднозначность задачи аппроксимации

Задача аппроксимации эмпирических зависимостей предполагает решение неопределенных и неоднозначных проблем (Problems under uncertainty), состоящих в следующем.

1. Реальность стохастической связи априорно неясна. Если она отсутствует или очень слабая, то аппроксимация вообще не имеет смысла.

Проблемы состоят в том, что реальность связи в общем случае оценивается корреляционным отношением, которое, в свою очередь, определяется суммой квадратов остатков искомой модели. Получается замкнутый круг проблем, из которого, строго говоря, нет выхода: прежде, чем строить модель необходимо установить реальность связи, но это делается по остаткам модели, которой пока нет.

2. Регулярная составляющая эмпирических данных явно не задана. Приближение к ней осуществляется, путем оптимизации расхождений осложненных случайными отклонениями данных с моделью, и обеспечения согласия распределений остатков и случайной составляющей эмпирических данных.

Например, вес младенца увеличивается буквально ежедневно. Динамика веса является важным показателем развития и здоровья ребенка. Однако при построении графика веса по эмпирическим данным заметны случайные отклонения, вызванные, предшествующим приемом пищи, мочеиспусканием, может быть, стулом и ошибками взвешиваний и т.п. Для анализа развития и здоровья ребенка модель должна отражать не результаты взвешиваний, а их регулярную составляющую, которая явно не задана. При этом расхождения результатов взвешивания с графиком должны соответствовать указанным случайным отклонениям.

3. Мера расхождений и метод приближения не заданы. Аппроксимацию можно выполнить минимизируя обсуждавшиеся (5), (6), (7) и другие меры расхождений. Исходя из статистических характеристик исходных данных, выбирается наиболее подходящая мера.

Влияние меры расхождений и метода приближения на эмпирическую зависимость видно из аппроксимации степенным полиномом 2-го порядка одних и тех же данных (рис. 3).

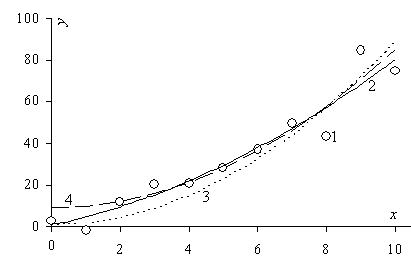
Рис. 3. Графики эмпирической зависимости по случайным данным (1) методами: 2 – наименьших квадратов; 3 – минимакса (по Чебышеву); 4 – наименьших модулей

4. Истинная модель эмпирической зависимости неизвестна, для ее построения необходимо подобрать подходящую функцию. Формально приближению, удовлетворяют многие функции (множество функций-претендентов) в общем случае – функциональные ряды.

На рис. 4 пример эмпирической зависимости силы тока I от сопротивления нагрузки R при напряжении 220  20 В со случайными отклонениями по нормальному закону.

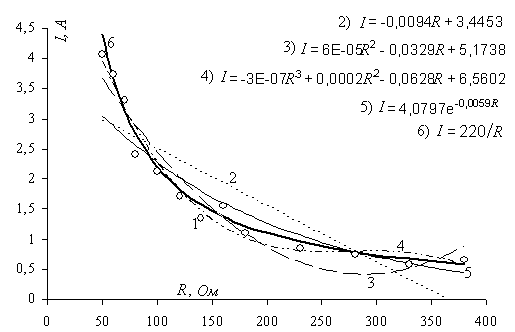
Рис. 4. Результаты аппроксимации эмпирической зависимости: 1– исходные данные; 2, 3, 4, 5, 6 – графики аппроксимирующих функций

Зависимость эмпирических данных (рис. 4 график 1) аппроксимирована функциями:

2) линейной в виде двух первых членов степенного ряда;

3) квадратичной в виде трех первых членов степенного ряда;

4) кубической в виде четырех первых членов степенного ряда;

5) экспоненциальной – из одного члена ряда

; (8)

6) дробно-рациональной (закона Ома) – одного члена ряда

I = , (9)

Все функции-претенденты с той или иной точностью удовлетворяют исходным данным, но линейная зависимость (рис.4, график 2) несколько нарушает общую тенденцию.

Наиболее подходящей, то есть близкой к истинной зависимости (1), является закон Ома (рис. 4, график 6). Однако, если природа эмпирической зависимости априорно неизвестна, то выбраковка других функций-претендентов не очевидна: требуется анализ приближения к явно незаданной регулярной составляющей и неизвестной истинной зависимости.

5. Количество членов аппроксимирующей функции подходящего класса, то есть порядок модели (степенного или другого ряда), который используется для приближения эмпирической зависимости, априорно неизвестен.

Закон Ома (1), отвечающий сущности обсуждавшейся эмпирической зависимости (рис. 4), является первым членом ряда дробно-рациональных функций (9), и правомерно поставить вопрос о подходящем числе m членов ряда.

В численном эксперименте при увеличении m мера расхождения (5) снижается с 0,39 для m = 1 до 0,20 для m = 6, (рис. 5, графики 2 и 3).

Если приближение в классе дробно-рациональных функций (9) принципиально не влияет на поведение аппроксимирующей функции, то приближение степенным рядом, при увеличении его порядка и снижении меры расхождения (5) с заданными исходными данными, сказывается на аппроксимирующих функциях (рис. 4, графики 2, 3, 4; рис. 5, график 4).

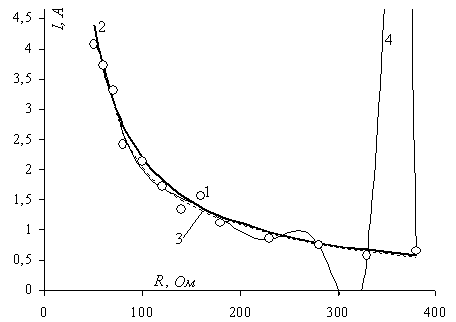
Рис. 5. Графики аппроксимации эмпирической зависимости:

1– исходные данные; 2 – функция (1); 3 – функция (9) при m = 6; 4 – степенной ряд 10 порядка

Степенной ряд 10-го порядка уменьшает меру расхождения до 0,16 в заданных точках, но между ними возникают нерегулярные (незакономерные) отклонения и разрывы (скачки), то есть суммирование всех членов является некорректным.

Следовательно, необходим выбор подходящего порядка аппроксимирующего ряда (его ограничение), то есть регуляризация по А.Н. Тихонову или ограничения по Р.И. Дубову.