2.2.4. Коэффициент корреляции – показатель силы линейной связи

Коэффициент корреляции k – ковариация при нормировании (х_i – )/_х и (y_i – )/_у:

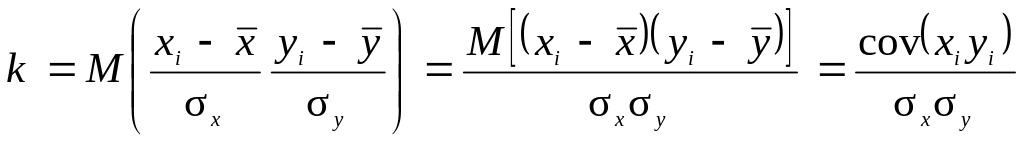. (2.11)

1. Коэффициент корреляции независимых случайных величин х и y равен нулю, так как в этом случае Cov (х_i, у_i) = 0. Случайные величины, для которых ковариация и коэффициент корреляции равны 0 линейно некоррелированы (линейно несвязанны).

Иными словами, если случайные величины независимы, то всегда

k = 0, (2.12)

но из того, что выполняется условие (2.12) не следует независимость случайных величин – можно говорить лишь об отсутствии между ними линейной связи (рис. 2.5).

Рис. 2.3. График y = х²

Пусть переменные связаны функциональной зависимостью y = х², график которой приведен на рис. 2.5 ( ). Вследствие симметрии каждому отклонению по оси абсцисс от среднего со знаком плюс отвечает такое же отклонение со знаком минус с одними и теми же отклонениями от среднего ординат, поэтому математическое ожидание смешанных произведений в формулах ковариации (2.8) и коэффициента корреляции (2.12) равно нулю. Следовательно, k = 0, хотя переменные связаны функциональной зависимостью y = х².

2. Коэффициент корреляции линейно связанных случайных величин х и y отличается от нуля (k  0), но находится в некоторых границах.

Существование границ коэффициента корреляции следует из дисперсии суммы зависимых случайных величин _ух + _хy. По определению их дисперсия

(2.13)

Поскольку дисперсия всегда положительна, то D(_ух + _хy) > 0. Из выражения (2.12) следует, что Cov(х_i, y_i) = _у_хk. С учетом этого из равенства (2.13) получается

1  k > 0 или –1  k  1. (2.14)

Таким образом, величина коэффициента корреляции находится в границах, определяемых неравенством (2.14). Как и для ковариации, знак k указывает:

– плюс – на возрастание линейной стохастической зависимости;

– минус – на убывание линейной стохастической зависимости.

Сами граничные значения k =  1 отвечают вырождению линейной стохастической зависимости в функциональную. В том случае, когда строго выполняется уравнение (2.1), то есть линейная зависимость является детерминированной, ковариация (2.9) определяется как

Cov(х_i, у_i) = M[(х_i – )(y_i – )] = M[(х_i – )(ax + b – a – b)] = aM[(х_i – )²] = a . (2.15)

Дисперсия линейной зависимости (2.1) составляет

D(ax + b) = M(ax + b – a – b) ² = a² . (2.16)

Так как ax + b = y, то D(ax + b) = , когда линейная зависимость детерминирована, и

_у=|a|_х, (2.17)

поэтому согласно формуле (2.11) с учетом выражений (2.15) и (2.16)

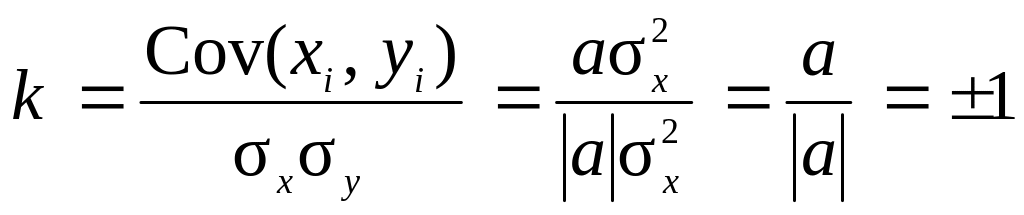. (2.18)

Очевидно, k = 1 соответствует линейно возрастающей функциональной зависимости с угловым коэффициентом a > 0, k = –1 – линейно убывающей функциональной зависимости с угловым коэффициентом a < 0.

3. Коэффициенты корреляции, регрессии и корреляционное отношение при линейной зависимости взаимосвязаны.

При нормальном распределении зависимой переменной y коэффициенты регрессии в уравнении линейной зависимости (2.1) удовлетворяют условию наименьших квадратов (5):

U(a, b) =  min, (2.19)

где сумма является функцией U(a, b) двух переменных (параметров a и b).

Из теоремы о необходимом и достаточном условии существования экстремума применительно к функции двух переменных U(a, b) следует система уравнений:

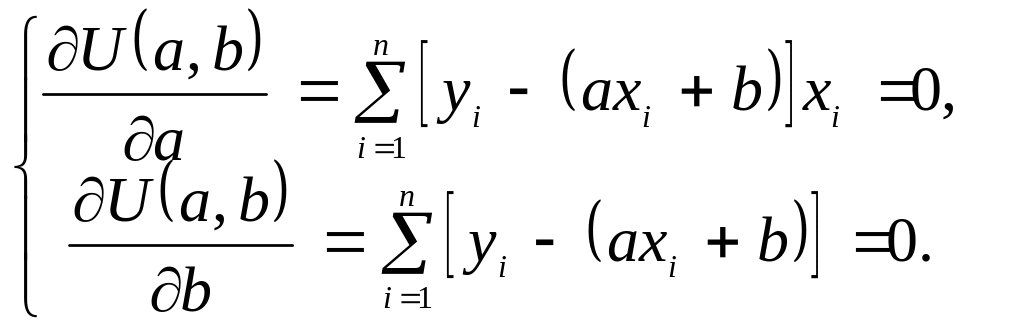(2.20)

Решение системы уравнений (2.20) позволяет определить коэффициенты регрессии:

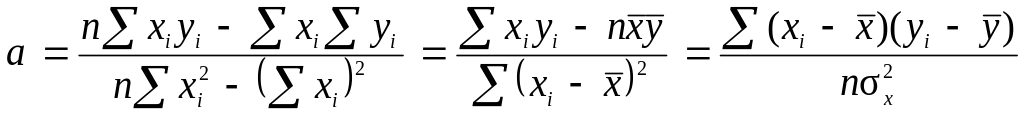. (2.21)

. (2.22)

Коэффициент корреляции (2.11) может быть представлен как

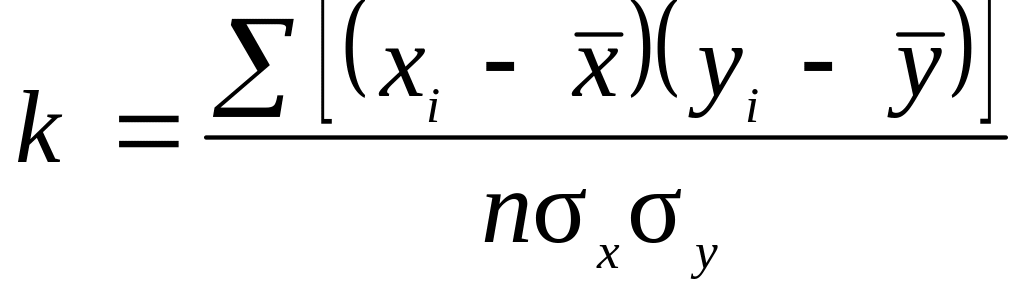. (2.23)

Из формул (2.21) и (2.23) следует связь коэффициентов регрессии и корреляции

, (2.24)

и, наоборот, коэффициент корреляции можно представить через коэффициент регрессии

. (2.25)

При линейной связи коэффициент корреляции равен корреляционному отношению, что следует из преобразований числителя выражения (2.7) с учетом соотношения (2.24):

(y_i – ax_i – b)² = (y_i – ax_i – –a )² = [(y_i – ) – a(x_i – )]² = (y_i – )² –

– 2 a(x_i – )(y_i – ) + a²(x_i – )² = (n – 1) – 2a(n – 1)k_х_у+ a²(n – 1) =

= (n – 1)[ – 2k + k² ] = (n – 1) (1 – k²). (2.26)

Полученное представление (2.26) позволяет упростить выражения 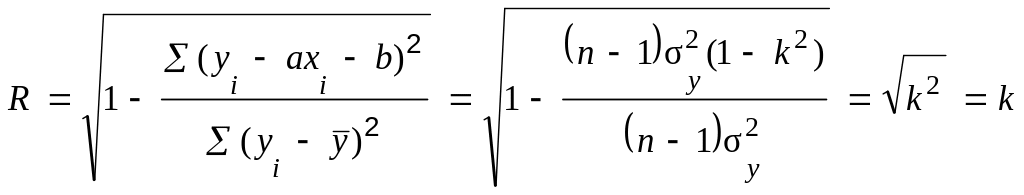(2.7)

, (2.27)

следовательно, параметры линейной зависимости связаны:

R = . (2.28)

4. Доверительный интервал выборочного коэффициента корреляции требует оценки, так как величина k определяется по формуле (2.11) с использованием случайных значений зависимой переменной y. Следовательно, выборочный коэффициент корреляции k, также является случайной величиной, которая может отличаться от нуля, даже если между переменными нет корреляции. Отсюда возникает необходимость проверки гипотезы о значимости отличия выборочного коэффициента корреляции k от нуля.

В такой суженной, но практически важной постановке задачи можно принять, что математическое ожидание коэффициента корреляции равно нулю, и случайные отклонения k подчиняются зависящему от объема выборки n так называемому r – распределению с нулевым математическим ожиданием (рис. 2.4).

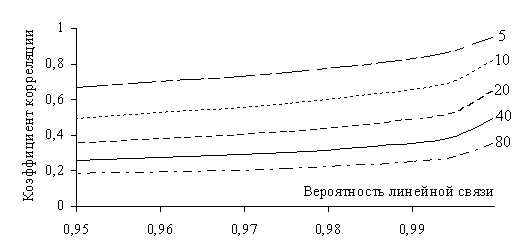
Рис. 2.4. Графики выборочных коэффициентов корреляции, как функций достоверности (вероятности) линейной связи в выборках объемом от 5 до 80 вариант (согласно r – распределения)

Из графиков (рис. 2.4) видно, что с обычно принимаемой вероятностью 0,95 линейная связь может полагаться значимой при абсолютных значениях выборочного коэффициента корреляции не менее 0,183 в выборке объемом 80 вариант; 0,257 – в случае 40 вариант; 0,360 – в случае 20 вариант и т.д.

При малом объеме выборки (около 5 вариант) даже значительный выборочный коэффициент корреляции |0,66| не является достоверным признаком реальности связи (рис. 2.4).

В выборках с более чем 20 вариантами доверительный интервал выборочного коэффициента корреляции k можно оценить по его среднеквадратичному отклонению s_k

(2.29)

от нулевого математического ожидания.

Для сравнения в таблице 2.1 при разных объемах выборок n приведены допустимые абсолютные отклонения выборочного коэффициента корреляции k_0,95, отвечающие достоверности линейной связи 0,95 и удвоенные среднеквадратичные отклонения s_k, рассчитанные по формуле (2.29).

Таблица 2.1

Оценки доверительного интервала k при достоверности линейной связи 0,95

n	5	10	20	40	80
k0,95	0,67	0,50	0,36	0,26	0,18
2 sk,	0,49	0,48	0,39	0,30	0,22

Из таблицы 2.1 видно, что в выборках объемом 10 вариант и более удвоенные среднеквадратичные отклонения s_k, рассчитанные по формуле (2.17), приближенно соответствуют допустимым абсолютным отклонениям выборочного коэффициента корреляции k_0,95 (при достоверности линейной связи 0,95).

Величина k – 3s_k (уменьшение на утроенный стандарт) может рассматриваться как гарантированный минимум, а величина k + 3s_k (увеличение на утроенный стандарт) – как гарантированный максимум оценки коэффициента корреляции с достоверностью линейной связи около 0,98.