1.1.2. Стохастическая эмпирическая зависимость случайных величин

Зависимость между случайными величинами называется стохастической (stochastic dependence). Она проявляется в изменении закона распределения одной из них (зависимой переменной) при изменении других (аргументов).

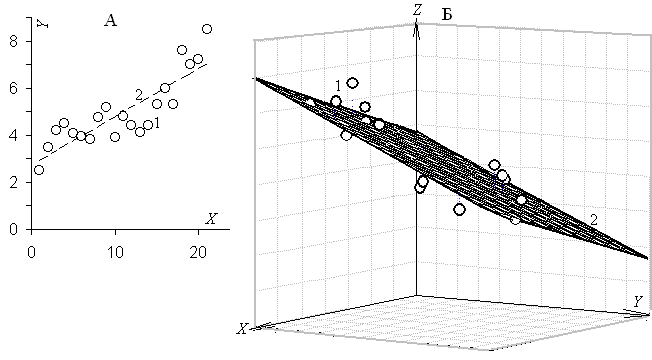
Рис. 1. Примеры стохастической эмпирической зависимости: А – парная связь, Б – многомерная (трехмерная) связь (1 – случайные значения зависимой переменной, 2 – тенденции поведения зависимой переменной при изменении аргументов)

Стохастическая эмпирическая зависимость графически, в системе координат зависимая переменная – аргументы, представляет собой множество случайно расположенных точек, которое отражает тенденцию поведения зависимой переменной при изменении аргументов (рис. 1).

Стохастическая эмпирическая зависимость с одним аргументом называется парной, если аргументов более одного, – многомерной, их примеры приведены на рис. 1.

В отличие от обычной функциональной зависимости, в которой изменениям значений аргумента (или нескольких аргументов) отвечает изменение детерминированной зависимой переменной, в стохастической зависимости при этом изменяется статистическое распределение случайной зависимой переменной, в частности, математическое ожидание (рис. 2).

Для парной связи на рис. 2 показано рассеяние зависимой переменной у(х), которое систематизировано для интервалов значений х и представлено гистограммами. Для трех интервалов значений х, приведены такие гистограммы распределения у(х) и кружками – их математические ожидания. Линия, проведенная вблизи точек математических ожиданий, отражает их зависимость от аргумента х и тенденцию поведения зависимой переменной.

Обычно стохастическая эмпирическая зависимость априорно не задана: неизвестно существует ли она вообще и каков ее вид.

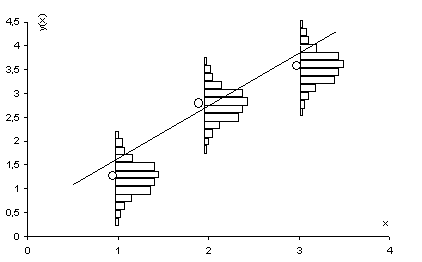
Рис. 2. Распределения зависимой переменной y(x) при x = 1, 2, 3

Построение стохастической эмпирической зависимости иначе называется математическим моделированием (аппроксимацией) или приближением и состоит в ее математическом выражении – представлении формулой (эмпирической функцией).

1.1.3. Математическая модель эмпирической зависимости и ее остатки

Эмпирически установленная формула (функция), которая отражает не всегда известную, но объективно существующую истинную зависимость и отвечает основному, устойчивому, повторяющемуся отношению между предметами, явлениями или их свойствами, рассматривается как математическая модель (mathematical model).

Устойчивое отношение вещей и их истинная зависимость, моделируются она или нет, существует объективно, имеет математическое выражение, и рассматривается как закон (физики, экономики и т.д.) или его следствие.

Если подходящие закон или следствие из него известны, то их естественно рассматривать в качестве искомой истинной зависимости и ее модели.

Например, эмпирическая зависимость:

– силы тока I от напряжения U и сопротивления нагрузки R следует из закона Ома

I = ; (1)

– спроса D на товар от дохода потребителя I и цены p описывается законом Стоуна

, (2)

где a и b – некоторые постоянные коэффициенты.

Коэффициенты, входящие в формулы и выражения и остающиеся постоянными в пределах условий рассматриваемой задачи, называются параметрами. В зависимости (2) a и b – параметры, постоянные для определенного товара и конкретных рыночных условий.

Чаще истинная зависимость переменных априорно неизвестна, необходимо ее обнаружить и, исходя из теоретических представлений, построить математическую модель соответствующей закономерности. При этом предполагается, что заданные значения переменных и их приращения на фоне случайных колебаний отражают математические свойства искомой истинной зависимости (поведение касательных, экстремумы, корни, асимптоты и т.п.).

Подбираемая аппроксимирующая функция сглаживает (усредняет) случайные колебания исходных эмпирических значений зависимой переменной и, подавляя тем самым случайную составляющую, является приближением к регулярной составляющей и, стало быть, к искомой истинной зависимости.

Разности моделируемых и эмпирических значений зависимой переменной называются остатками модели (residuals). В идеале, когда модель адекватна искомой истинной зависимости и отвечает регулярной составляющей исходных значений, их случайная составляющая соответствует остаткам.

Случайная составляющая исходных значений и остатки являются случайными величинами, и их соответствие характеризуется:

– согласием их статистических распределений;

– случайностью последовательности остатков, то есть отсутствием между ними связи (автокорреляции).

Искомая истинная зависимость неизвестна, и в качестве необходимого условия адекватности модели используется соответствие статистических свойств остатков и случайной составляющей.

Математическая модель эмпирической зависимости:

– позволяет установить адекватность экспериментальных данных тому или иному известному закону или выявить новые закономерности;

– решает для зависимой переменной задачи интерполяции внутри заданного интервала значений аргумента и прогнозирования (экстраполяции) за пределами интервала.