3.2.5. Оценки качества линейной модели

Качество линейной модели характеризуется ее соответствием неизвестной, но объективно существующей истинной зависимости, и доверительными границами соответствия.

1. Доверительные интервалы оценок коэффициентов регрессии вычисляются через дисперсии по формулам (2.34), (2.65) и (2.67).

Доверительные интервалы линии регрессии и прогнозируемой зависимой переменной у включают дисперсию D₂, рассчитываемую по формуле (2.34).

По дисперсиям оценок параметров регрессии вычисляются стандарты:

= 0,629  0,052 и = – 8,203  2,142.

Выборочные коэффициенты регрессии по абсолютной величине превышают среднеквадратичные погрешности оценивания в несколько раз и позволяют отклонить нулевую гипотезу. Однако погрешности оценивания параметров регрессии обуславливают ее случайное отклонение от истинной зависимости с неизвестными точными значениями параметров.

2. Доверительные границы линии регрессии (y₊ и y_–) рассчитываются по формулам (2.84) и (2.85) для всех х. Величину t рекомендуется определить для вероятности 99%.

3. Доверительные границы прогнозируемой переменной y, то есть y’₊ и y’_–, вычисляются по формуле (2.85) для всех х с указанной выше величиной t.

По результатам расчетов строятся графики, как показано на рис. 2.07.

Графики (рис. 2.07) показывают, что хотя линейная зависимость значима:

– положение линии регрессии случайно и колеблется в доверительной области;

– предсказываемые моделью цены являются приближенными (попадают в доверительные границы) и реальны при выдержке вина более 15 лет;

– модель неадекватна заметным нелинейным проявлениям аукционного ценообразования, и допускает нереальную экстраполяцию цен в отрицательную область при выдержке вина менее 15 лет.

3.2.6. Оценка регрессии и ее качества встроенной функцией линейн

Встроенная функция ЛИНЕЙН решает методом наименьших квадратов задачи линейной множественной и, в частности, двухмерной регрессии.

В частном случае двухмерной линейной регрессии ее уравнение рассматривается, как

y = mx + b, (3.2)

где: y – линейная функция независимой переменной x;

m – коэффициент при независимой переменной x;

b – свободный член.

Функция ЛИНЕЙН возвращает массив параметров регрессии и дополнительную статистику. Синтаксис функции

ЛИНЕЙН(известные_значения_y;известные_значения_x;конст;статистика)

где: известные_значения_y – множество значений зависимой переменной y (один столбец или одна строка);

известные_значения_x – множество значений независимой переменной x, соответствующих значениям зависимой переменной y;

конст – логическое значение: если конст – ИСТИНА (равно 1) или опущено, то b вычисляется, Если конст – ЛОЖЬ (равно 0), то b полагается равным 0, и рассматривается уравнение регрессии y = mx;

статистика – логическое значение: если статистика – ИСТИНА (равно 1), то возвращается дополнительная регрессионную статистика, если статистика – ЛОЖЬ (равно 0) или опущена, то функция возвращаются только коэффициент m и постоянная b.

Функция ЛИНЕЙН является функцией массивов и возвращает не одно значение, а несколько – массив параметров, под которые предварительно выделяется (засвечивается) диапазон ячеек – в двухмерном случае из 2-х столбцов по 5 строк. Только после этого вызывается Мастер функций.

В диалоговом окне функции заполняются поля, и затем нажимается комбинация клавиш Ctrl, Shift и Enter. При этом функция ЛИНЕЙН возвращает в выделенный диапазон, если статистика – ИСТИНА, массив данных, приведенный на рис. 3.4.

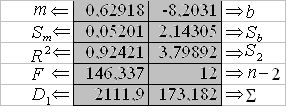
Рис. 3.4. Массив данных, возвращаемый функцией ЛИНЕЙН

Возвращаемые данные в виде двух столбцов на рис 3.4 затонированы и их смысл поясняется символами (слева и справа от массива данных):

m – коэффициент при независимой переменной x в уравнении (3.2);

b – свободный член в уравнении (3.2);

S_m – среднеквадратичная погрешность оценки коэффициента m;

S_b – среднеквадратичная погрешность оценки свободного члена b;

S₂ – стандарт рассеяния зависимой переменной y относительно регрессии;

R² – квадрат корреляционного отношения (коэффициента корреляции)

n – 2 – число степеней свободы n отклонений зависимой переменной y относительно линейной регрессии;

D₁ – дисперсия зависимой переменной y в модели – имеет одну степень свободы;

F – отношение дисперсий D₁ /D₂;

 – сумма квадратов отклонений зависимой переменной y относительно линейной регрессии, определяющая дисперсию D₂ и стандарт S₂.

Смысл отношения дисперсий D₁ /D₂ следует из уравнений (2.32) и (2.40)

Adjusted R²  R² = k² = 1 –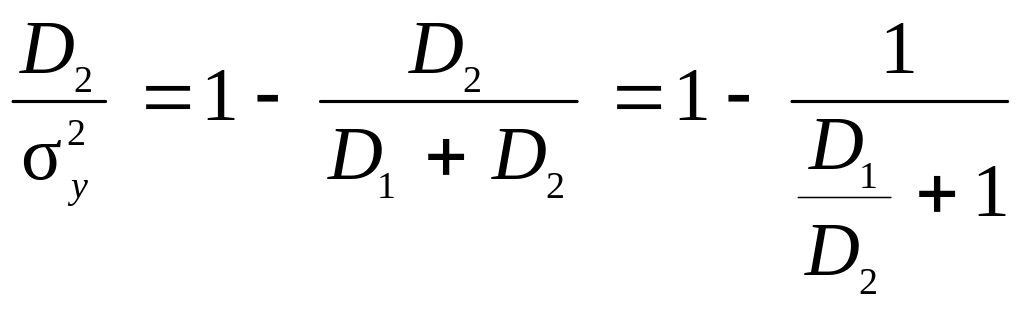 . (3.3)

Из выражения (3.3) видно:

– если D₁ /D₂  0, то Adjusted R²  R² = k²  0, то есть линейная связь отсутствует;

– если D₁ /D₂  , то Adjusted R²  R² = k²  1, следовательно, линейная стохастическая связь максимальна и вырождается в функциональную.

Очевидно, чем больше отношение дисперсий D₁ /D₂, тем значимее значения Adjusted R²  R² = k² и теснее линейная связь.

Отношение D₁ /D₂ подчиняется F-распределению, которое позволяет проверить нулевую гипотезу о равенстве F = 1, что является более сильным условием по сравнению с F  0. Если отклоняется условие F = 1, то тем более есть основание отклонить равенство F = 0.

В рассматриваемом случае (рис. 3.4) функция ЛИНЕЙН возвращает значение F = 146,337. Вероятность ошибки того, что F  1, то есть отклонения нулевой гипотезы, возвращается функцией =FРАСП(146,337;1;12), и практически равна нулю. Минимальная критическая величина F для отклонения нулевой гипотезы с доверительной вероятность 95% (вероятностью ошибки 5%) возвращается функцией =FРАСПОБР(0,05;1;12) = 4,747.

Следовательно, по критической величине F и вероятности ошибки при отклонении нулевой гипотезы для фактической величины F можно сделать вывод о значимости обсуждаемой линейной связи.