2.3.2. Максимально правдоподобные меры расхождения

Максимально правдоподобная мера расхождения и соответствующий метод приближения определяется распределением случайной составляющей исходных данных.

1. Максимально правдоподобная мера расхождения и метод приближения при нормальном распределении случайной составляющей находятся следующим образом.

Пусть эмпирические данные y_i состоят из неизвестных истинных значений (регулярной составляющей) y_0i, к которым выполняется приближение линейной функции (x _i), и случайных колебаний (случайной составляющей) y_i, то есть

y_{i =} y_{i –} y_{0i =} y_{i –} (x _i)_{. (2.41)}

Если значения случайной составляющей распределены нормально с нулевым математическим ожиданием и стандартом , то плотность вероятностей y_i записывается, как

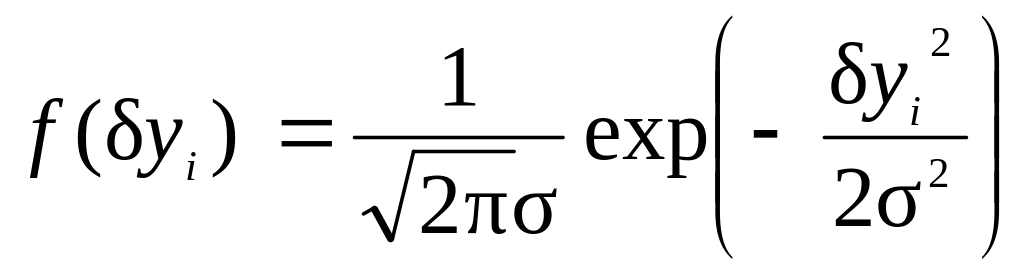. (2.42)

С учетом значения (2.41) из функции (2.42) следует:

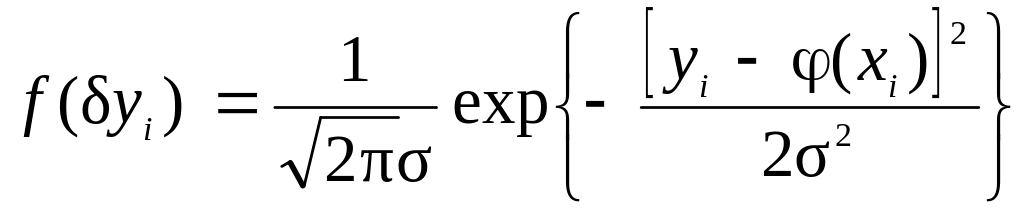. (2.43)

Для n вариант совместная плотность вероятностей случайных отклонений y_i является произведением плотностей вероятностей (2.43):

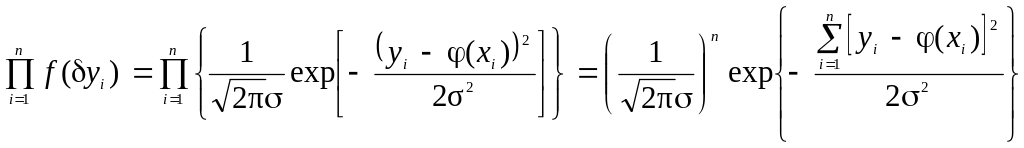(2.44)

Совместная плотность вероятностей (2.44) образует функцию правдоподобия. Ее максимум (или ее логарифма) отвечает наиболее эффективной оценке параметров (x_i). Из функции правдоподобия (2.44) следует, что ее максимум достигается при условии:

 min. (2.45)

Следовательно, при нормальном распределении случайной составляющей зависимой переменной минимизируемая сумма квадратов отклонений эмпирических значений зависимой переменной от аппроксимирующей функции является наиболее подходящей мерой приближения. Минимизация такой меры отвечает методу наименьших квадратов.

2. Мера и метод приближения эмпирической зависимости при повышенном числе больших уклонений в случайной составляющей определяются по принципу максимального правдоподобия.

Повышенное количество больших уклонений по сравнению с нормальным законом имеет, в частности, двустороннее экспоненциальное распределение, известное как распределение Лапласа. Его плотность вероятностей затухает как , а в нормальном законе, как , поэтому при больших уклонениях x их вероятность повышено у распределения Лапласа.

В соответствии с этим зависимая переменная эмпирических данных y_i полагается состоящей из неизвестных истинных значений y_0i, к которым сходится аппроксимирующая функция (x _i), и случайных отклонений y_i, распределенных по закону Лапласа.

Распределение Лапласа является симметричным, имеет нулевое среднее и при обозначении дисперсии 2/, плотность вероятностей имеет вид:

, – < y_i < . (2.46)

С учетом выражения (2.41) функция (2.46) записывается в виде

. (2.47)

Для n независимых вариант совместная плотность вероятностей случайных отклонений y_i является произведением плотностей вероятностей (2.47):

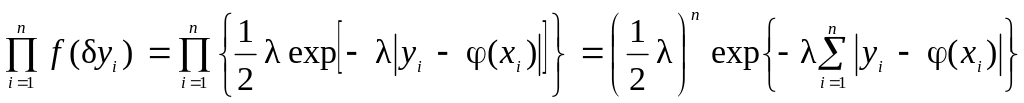. (2.48)

Плотность вероятностей (2.48) является функцией правдоподобия, максимум которой отвечает наиболее эффективной оценке параметров (x_i).

Из функции правдоподобия (2.48) следует, что ее максимум достигается при условии:

 min. (2.49)

Следовательно, если зависимая переменная включает случайную составляющую с повышенным количеством больших уклонений, как в двухстороннем экспоненциальном распределении, наиболее подходящей мерой приближения является минимизируемая сумма абсолютных отклонений эмпирических значений зависимой переменной от аппроксимирующей функции. Минимизация такой меры – метод наименьших модулей или Лагранжа.

3. Мера и метод приближения эмпирической зависимости при равномерном распределении случайной составляющей также определяются, исходя из принципа максимального правдоподобия.

Равномерное симметричное относительно нуля рассеяние случайных величин y_i в пределах |y_max| отвечает прямоугольному распределению с плотностью вероятностей

, –y_max < y_i < y_max. (2.50)

Здесь зависимая переменная эмпирических данных y_i полагается состоящей из неизвестных истинных значений y_0i, к которым сходится аппроксимирующая функция (x _i), и равномерно распределенных случайных отклонений y_i, как в соотношении (2.41).

Для n независимых вариант совместная плотность вероятностей случайных отклонений y_i является произведением плотностей вероятностей (2.50):

. (2.51)

Плотность вероятность (2.51) является функцией правдоподобия с максимумом, отвечающим наиболее эффективной оценке параметров (x_i).

Очевидно, максимум функции (2.51) достигается при условии:

|y_max|  min, (2.52)

то есть

|y_{i –} (x _i)| _max  min (2.53)

Следовательно, если зависимая переменная включает случайную составляющую, распределенную равномерно, наиболее подходящей мерой приближения является минимизируемое максимальное абсолютное отклонение эмпирических значений зависимой переменной от аппроксимирующей функции. Этот метод называется минимаксным или равномерного приближения по Чебышеву.

4. Компромиссные мера и метод приближения эмпирической зависимости по Джексону, состоит в минимизации суммы степеней 3/2 абсолютных отклонений эмпирических значений зависимой переменной от аппроксимирующей функции:

 min. (2.54)

Мера Джексона является промежуточной между квадратичной и модульной мерами, которые эффективны для рассеяний случайной составляющей по нормальному закону и по распределению Лапласа.

Смысл меры Джексона состоит в том, чтобы ослабить влияние больших случайных отклонений, при их количестве, меньшем, чем в распределении Лапласа, но превышающем встречаемость при нормальном законе.

5. Мера и метод приближения эмпирической зависимости при отсутствии информации о законе распределения случайной составляющей предложены Р. И. Дубовым.

При отсутствии сведений о законе распределения случайной составляющей зависимой переменной Р. И. Дубов предложил выбирать тип зависимости и ее параметры по максимуму числа чередований фактических данных относительно аппроксимирующей кривой. При использовании данного подхода приближение строиться из условия наибольшего числа пересечений отрезков, которые соединяют смежные точки фактических данных, аппроксимирующей кривой. Из моделей с разным количеством параметров предпочтение отдается модели, у которой больше разность максимального числа пересечений и наложенных связей.

Метод Дубова устойчив при любом распределении случайной составляющей зависимой переменной, но за отсутствие информации о типе распределения приходится платить неоднозначностью аппроксимации. Максимальному числу чередований с одним и тем же количеством степеней свободы отвечают не конкретные значения параметров, а их интервалы.

Оригинальная идея Р. И. Дубова исходит из интуитивно напрашивающихся представлений о случайном равномерном рассеянии отклонений относительно аппроксимирующей линии. Хотя такой подход в некоторых условиях оправдан, на практике необходимо учитывать, что при рассеянии типа случайных блужданий, например, в серии бросаний монеты, строгого чередования «орлов» и «решек» обычно не происходит, а количества тех и других не совпадают. Поэтому, как правило, в таких играх один игрок выигрывает, а другой проигрывает, то есть ничейный исход не является наиболее вероятным.