1.3.3. Оптимальное приближение эмпирической зависимости

Приближение рассматривается как оптимальное, если оно удовлетворяет изложенной постановке задачи аппроксимация эмпирической зависимости в условиях обсуждавшейся неопределенности и неоднозначности. Для этого требуется, прежде всего, установить само существование связи и, если она реальна, определить:

– меру расхождений и метод приближения;

– класс аппроксимирующей функции (некоторый функциональный ряд);

– порядок модели (число членов ряда);

– распределение остатков.

Решения этих проблем, необходимых для оптимального приближения, реализуются по определенным правилам, которые составляют целостную систему принципов и алгоритмов оптимальной аппроксимации эмпирических зависимостей, рассматриваемых далее отдельно для парных линейных, нелинейных и многомерных функций.

2. Основы линейного приближения стохастической зависимости

Линейное приближение является самым простым случаем стохастической связи.

2.1. Задача линейного приближения при парной связи

В задаче линейного приближения вид математических моделей предопределен.

2.1.1. Виды математических моделей парной линейной зависимости

Общее уравнение парной линейной зависимости имеет вид

y = ax + b, (2.1)

где: x – независимая; y – зависимая переменная; a и b – параметры (коэффициенты).

Частными случаями общего уравнения (2.1) являются:

y = ax при b = 0; (2.2)

y = b при a = 0; (2.3)

y = 0 при a = 0 и b = 0; (2.4)

x = 0 при a = 1, b = 0 и y = 0 (2.5)

Линейные зависимости, задаваемые уравнениями (2.1), (2.2), (2.3), (2.4) и (2.5), отображаются семейством линейных графиков (рис. 2.1).

Эмпирические данные x и y состоят из истинных, явно не выделенных, значений некоторых характеристик (регулярной составляющей), которые рассматриваются как детерминированные, и случайных отклонений (случайной составляющей), вызванных влиянием неучитываемых факторов и ошибками измерений x и y. При этом независимая переменная x полагается условно детерминированной, а ее случайные колебания переносятся на зависимую переменную y.

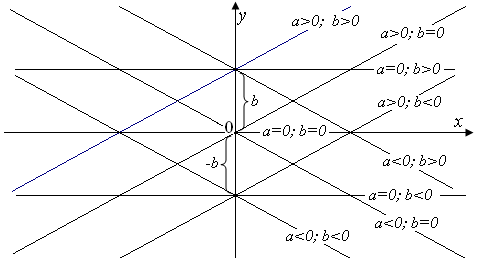
Рис.2.1. Графики зависимостей y = ax + b при различных значениях коэффициентов a и b

2.1.2. Неопределенность задачи построения линейной модели

Общая неопределенность задачи аппроксимации для линейной модели, несмотря на ее предопределенность (2.1), полностью не устраняется. Не определены, в частности:

– истинные значения эмпирических данных (их регулярные составляющие), зависимость которых моделируется;

– реальность (значимость) линейной зависимости между характеристиками x и y рассматриваемого явления (априорно это неизвестно);

– подходящая мера расхождений и метод оценки параметров a и b;

– состав формулы линейной зависимости (2.1), которая может иметь вид (2.2) – (2.5);

– оптимальность именно линейной модели, то есть ее предпочтительность по сравнению с нелинейной аппроксимацией;

– адекватность линейной модели искомой истинной зависимости.

Эти вопросы не имеют определенных и однозначных решений, и задача приближения парной эмпирической зависимости, даже в простейшем линейном случае, – problems under uncertainty (неопределенная задача), предполагающая построение оптимального решения.

Как указывалось, очень точное приближение к эмпирическим данным, отнюдь, не является оптимальным. Более того, слишком хорошее приближение к эмпирическим данным, содержащим ошибки измерения, указывает на несоответствие модели истинным значениям.