2.4.2. Доверительные интервалы линейной эмпирической зависимости

Обсуждавшиеся выше случайные колебания оценок параметров (углового коэффициента и свободного члена), которые находятся методом наименьших квадратов по эмпирическим данным, вызывают случайные отклонения самой линии регрессии от истинной линейной зависимости с неизвестными точными значениями параметров.

Дисперсия линии регрессии, обозначаемая далее, как D(y), складывается из дисперсий параметров D( ) и D( ), вычисляемых по формулам (2.65) и (2.67). Однако при этом необходимо учитывать, что параметры и , определяемые методом наименьших квадратов, являются зависимыми величинами. В этом случае дисперсии D( ) и D( ) суммируются по правилам для зависимых случайных величин.

1. Взаимозависимость параметров линейной регрессии следует из уравнения (2.55). При средних значениях переменных и уравнение (2.55) записывается как

, (2.77)

и позволяет представить параметр в виде функции другого параметра :

. (2.78)

В уравнении (2.78): – зависимая переменная; – независимая переменная; – угловой коэффициент; – свободный член.

В соответствии с уравнениями (2.28) и (2.78) коэффициент корреляции между и , как переменными, можно представить в виде

. (2.79)

Ковариация между переменными и выражается через коэффициент корреляции (2.79) в соответствии с уравнением (2.18):

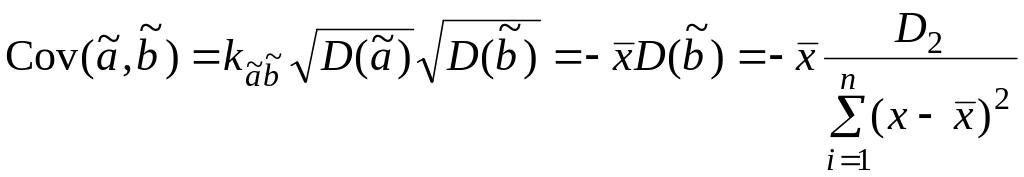. (2.80)

2. Дисперсия эмпирической линейной функции (2.55), вызванная случайными колебаниями параметров, определяется с учетом связи между ними (2.80). Дисперсия свободного члена отвечает выражению (2.67); дисперсия произведения есть , поскольку х рассматривается как постоянная, следовательно:

D(y) = D( ) + 2Cov( , ) + х²D( ) = D( ) + 2Cov( , )х + х²D( ). (2.81)

Подстановка выражений (2.65), (2.67) и (2.80) в дисперсию линейной функции (2.82) приводит к уравнению

D(y) = . (2.82)

Из выражения (2.82) видно, что дисперсия является функцией независимой переменной х – параболой с минимумом при х = . При отклонении от нее в обе стороны дисперсия увеличивается и уменьшается точность прогноза.

3. Доверительная область графика регрессии ограничивается отстоящими от нее линиями на удалении 2-х или 3-х стандартов s(y), определяемого из дисперсии (2.82):

s(y) = . (2.83)

При нормальном распределении случайной составляющей зависимой переменной ограничение линиями 2s(y) охватывает около 95% возможных отклонений от математического ожидания (графика регрессии). Ограничение линиями 3s(y) включает 99,7% отклонений.

Если объем данных n < 30, взятых из нормальной генеральной совокупности, то отношение отклонения зависимой переменной от математического ожидания (линии регрессии) к стандарту, имеет t-распределение Стьюдента.

Вероятность в t-распределении Стьюдента зависит от числа степеней свободы, которое при линейной регрессии с 2 параметрами равно n – 2. Для малых выборок t-отношение (и доверительная область) возрастает при уменьшении числа степеней свободы.

В соответствии с этим, исходя из выражения дисперсии (2.82) и соответствующего ей стандарта, доверительная граница сверху в общем случае описывается уравнением

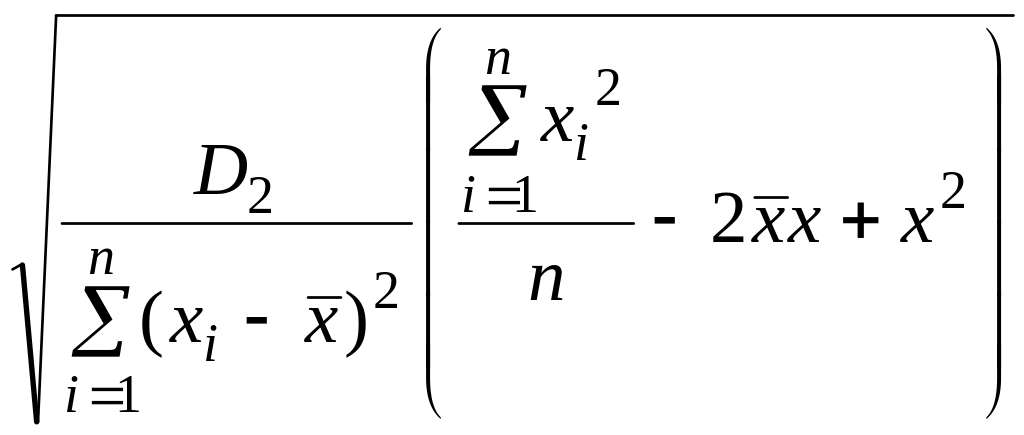y₊ = x + + t , (2.84)

доверительная граница снизу

y_– = x + – t , (2.85)

где t – число стандартов в больших выборках (2 или 3), в малых выборках – берется по t-распределению

Графики функций (2.84) и (2.85), ограничивающих доверительную область, – гиперболы, проходящие первая выше, вторая – ниже линии регрессии (2.55), как на рис. 2.7.