2.2.5. Коэффициент детерминации – показатель определенности связи

Реальность и теснота стохастической связи х и у, в том числе линейной, характеризуется показателем определенности, или коэффициентом детерминации, определяемым, как отношение дисперсии зависимой переменной у, объясненной моделью, к общей дисперсии этой переменной.

Иными словами, коэффициент детерминации есть доля дисперсии, объясненной моделью, в общей дисперсии зависимой переменной и выражается в %.

Структура коэффициента детерминации, его связь с корреляционным отношением и коэффициентом корреляции вытекают из дисперсии зависимой переменной у.

1. Общая дисперсия зависимой переменной у определяется, как

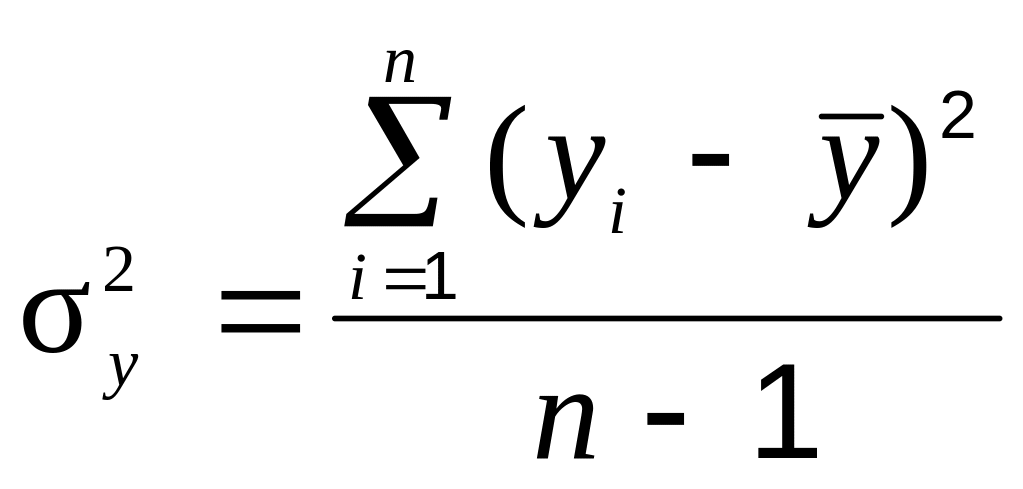. (2.30)

Общая дисперсия (2.30) – это сумма квадратов отклонений всех n значений зависимой переменной y_i от среднего , поделенная на число степеней свободы n-1 суммы отклонений с учетом того, что на них наложено 1 условие:

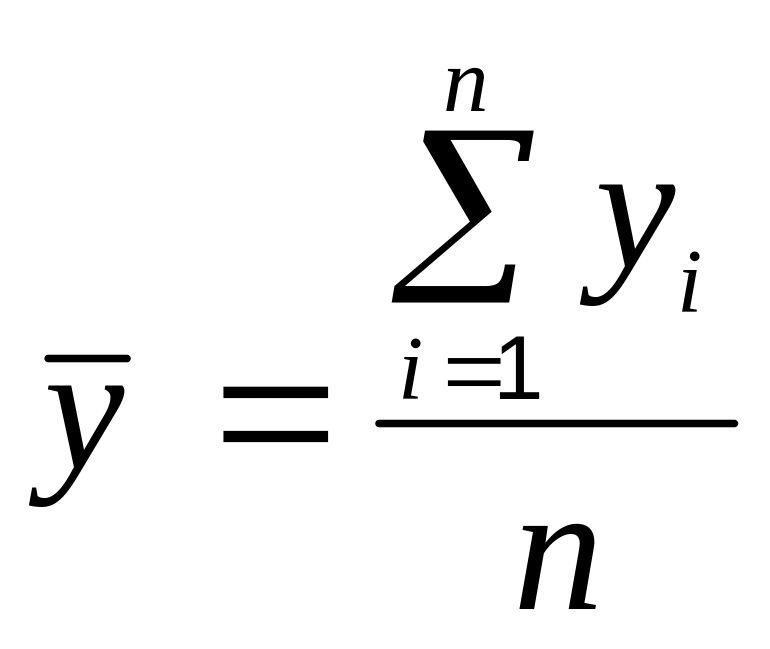. (2.31)

Общая дисперсия (2.30) зависимой переменной y по правилам операций с дисперсиями разлагается на две составляющие:

= D₁ + D₂, (2.32)

где: D₁ – дисперсия зависимой переменной y в модели (2.1) относительно среднего ;

D₂ – дисперсия зависимой переменной y относительно модели (2.1).

2. Дисперсия зависимой переменной в модели при линейной связи y_i = ax_i + b, представляет собой по определению математическое ожидание суммы квадратов разностей, но с учетом их детерминированного характера:

– независимая переменная x_i полагается детерминированной (ее случайные отклонения относятся на зависимую переменную);

– математическое ожидание детерминированной величины, в частности суммы квадратов разностей, равно ей самой, поэтому:

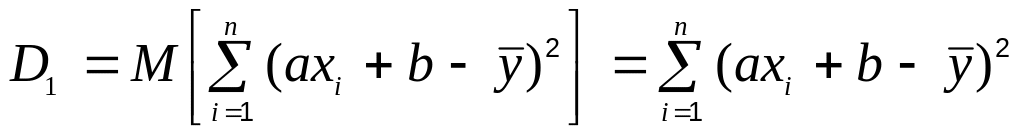. (2.33)

Следовательно, дисперсия D₁ имеет одну степень свободы.

3. Дисперсия отклонений зависимой переменной относительно модели, в данном случае линейной зависимости (2.1), есть

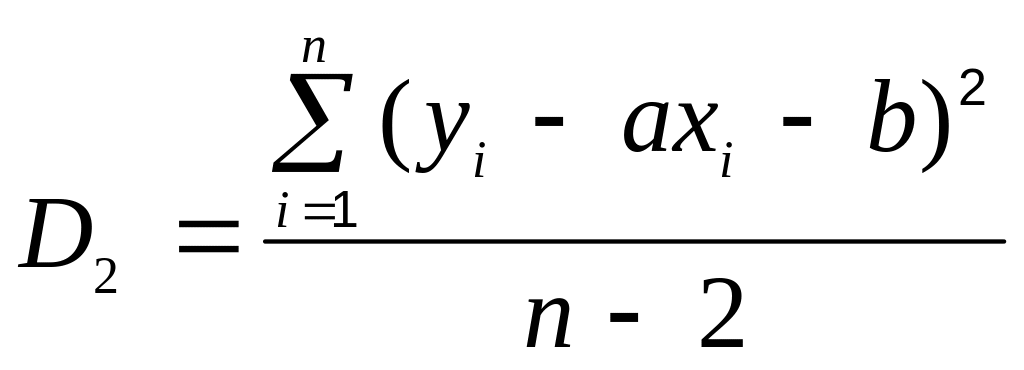, (2.34)

где число степеней свободы n – 2 равно объему выборки без 2 связей, входящих в параметры уравнения (2.1).

4. Выражения коэффициента детерминации в соответствии с его определением, дисперсией (2.30) и ее составляющими (2.33) и (2.34) имеет вид:

D₁ / = ( – D₂) / = 1 - D₂ / . (2.35)

По формулам (2.30), (2.34) и (2.7) коэффициент детерминации (2.35) иначе будет

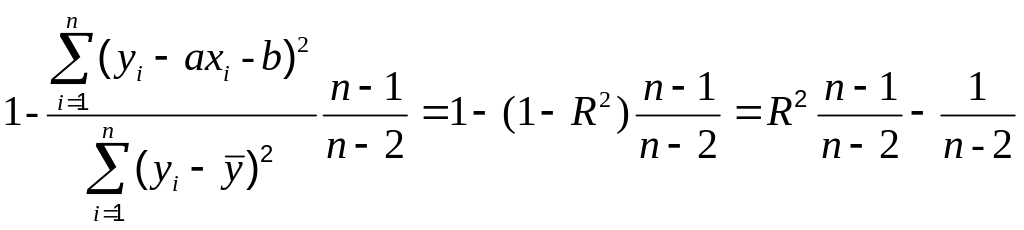. (2.36)

Коэффициент детерминации (2.36), в отличие от корреляционного отношения (2.7), является несмещенной оценкой тесноты связи, поскольку рассчитывается с учетом числа степеней свободы. Поэтому при любом объеме выборки оценка коэффициента детерминации равна математическому ожиданию выражения (2.36).

В программных средствах выводятся квадрат корреляционного отношения R² и коэффициент детерминации Adjusted R² – откорректированный R² с учетом числа степеней свободы. При линейной связи Adjusted R² совпадает с выражением (2.36) и дается обычно в %:

Adjusted R² = 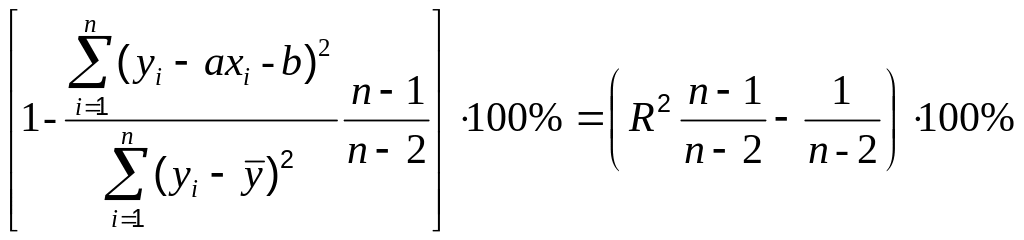. (2.37)

Поскольку коэффициент корреляции при линейной связи равен корреляционному отношению (2.28), то коэффициент детерминации (2.37) можно представить как

Adjusted R² = . (2.38)

В больших выборках (при n > 30) можно пренебречь поправками, учитывающими число степеней свободы, и приближенно полагать

Adjusted R²  R² = k². (2.39)

Графически связь (2.39) коэффициента корреляции с Adjusted R² показана на рис. 2.5.

Из графика (рис. 2.5) следует, что, казалось бы, тесная связь, когда коэффициент корреляции 0,7, объясняет только 49% дисперсии зависимой переменной.

Когда модель полностью объясняет общую дисперсию (обе дисперсии одинаковы), коэффициент детерминации равен максимально возможной величине (100%), что соответствует вырождению стохастической зависимости в функциональную связь (рис. 2.2В);

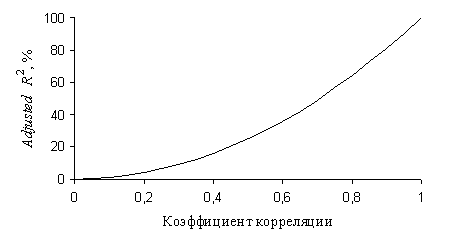
Рис. 2.5. График зависимости доли объясненной дисперсии от тесноты связи

Если модель совершенно не объясняет общую дисперсию, то есть моделирование не уменьшает рассеяния, коэффициент детерминации равен минимальной величине (0%,) и стохастической зависимости нет (рис. 2.2А);

В общем случае, при частичном объяснении общей дисперсии, доля объясненной дисперсии (и коэффициент детерминации) находится между минимальной (0%) и максимальной величиной (100%), и характеризует силу стохастической зависимости (рис. 2.2Б).

5. Оценка достоверности коэффициента детерминации и существования стохастической связи может быть построена на основе выражения (2.36)

Adjusted R² =1 – D₂ / . (2.40)

Из выражения (2.41) следует, что коэффициент детерминации равен нулю и стохастическая связь отсутствует, когда отношение дисперсий D₂ / = 1, то есть дисперсии зависимой переменной y относительно модели и среднего одинаковы.

Стало быть, оценка достоверности коэффициента детерминации и реальности стохастической связи сводится к проверке нулевой гипотезы о том, что D₂ / = 1, что делается при помощи F-распределения Фишера.

F-распределение табулировано для отношения большей дисперсии к меньшей (в данном случае / D₂) и зависит от степеней свободы каждой дисперсии (f₁ = n – 1 и f₂ = n – 2), то есть F-вероятность – функция 3 переменных F( / D₂, f₁, f₂). График F-вероятности при объеме выборки n = 22 приведен на рис. 2.6.

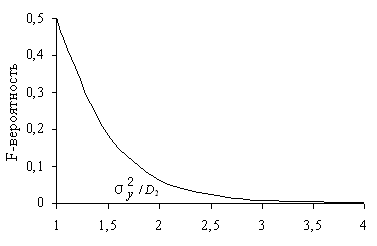
Рис. 2.6. График F-вероятности со степенями свободы f₁ = 21 и f₂ = 20

Вероятность F-распределения, имеет максимум при / D₂ = 1 и плавно затухает до 0 с увеличением отношения / D₂.

Равенство / D₂ = 1 носит вероятностный характер, поскольку оценки дисперсий являются случайными величинами. Поэтому оценка / D₂ может отличаться от 1 при равенстве истинных значений дисперсий и требуется установить значимость их различия. Обычно нулевая гипотеза о равенстве / D₂ = 1 отклоняется при вероятности менее 0,05. Иными словами, допускается вероятность ошибки отклонения нулевой гипотезы, то есть того, что > D₂, не превышающая 0,05. Принятая вероятность отклонения гипотезы называется критическим уровнем. При его выборе необходимо учитывать, что критический уровень менее 0,05 уменьшает вероятность ошибки отклонения нулевой гипотезы (ошибки первого рода), но возрастает вероятность ошибки принятия нулевой гипотезы (ошибки второго рода) и отклонения неравенства > D₂, если оно есть и стохастическая связь реальна.

Случаи / D₂ < 1 невозможны, так как при положительных слагаемых (2.33) сумма всегда больше любого слагаемого.

Проблема вероятностной оценки отношения и проверки нулевой гипотезы возникает при / D₂ > 1. Малозначимое различие с принятой вероятностью ошибки отклонения нулевой гипотезы означает, что стохастическая связь отсутствует.

Практически возможны два способа решения задачи, которые можно рассмотреть на примере стохастической связи случайных величин х и y в выборке объемом n = 22.

Пусть дисперсии, вычисленные по формулам (2.31) и (2.34), образуют отношение / D₂ = 2,12 со степенями свободы для общей дисперсии f₁ = n – 1 = 21 и второй дисперсии f₂ = n – 2 = 20.

В первом способе ищется вероятность F-распределения при указанных параметрах: / D₂ = 2,12 со степенями свободы f₁ = 21, f₂ = 20. Искомая вероятность составляет 0,049. Поскольку 0,049 < 0,050, то нулевая гипотеза о равенстве дисперсий отклоняется и полагается, что стохастическая связь реальна.

Второй способ состоит в оценке отношения / D₂ (по таблице или при возвращении обратной функцией) для f₁ = 21, f₂ = 20 при критическом уровне вероятности 0,05. Искомое минимально допустимое отношение составляет 2,11.

Поскольку 2,12 > 2,11, то есть вывод аналогичен указанному выше.