2.2. Оценка реальности парной линейной связи и ее тесноты

Первоочередным вопросом построения линейной эмпирической зависимости является оценка реальности линейной связи (первое правило). Если связи нет, задача линейной аппроксимации не имеет решения, и оно прекращается.

Сложность оценки существования связи состоит в том, что она завуалирована случайным рассеянием переменных, то есть не очевидна.

2.2.1. Случайное рассеяние и неопределенность парной линейной связи

Причиной случайного рассеяния эмпирических данных является влияние множества неучитываемых факторов и ошибок измерений.

1. Случайное рассеяние при линейной зависимости проявляется в том, что каждое допустимое значение аргумента х обуславливает не определенную величину зависимой переменной у(х), а множество ее случайных значений (точек в системе координат х0у). Пример такого рассеяния переменных приведен на рис. 1А.

Множество случайных значений у(х) для каждого значения х образует статистическое распределение, а для ряда значения х – семейство распределений. На рис. 2 такое семейство распределений представлено семейством гистограмм, отвечающим некоторой линейной стохастической связи. Она проявляется в изменении закона распределения зависимой переменной, в частности математических ожиданий, при изменении аргумента.

2. Неопределенность стохастической связи в математической статистике понимается как показатель рассеяния (разброса) случайных величин, отсутствия у них общей тенденции. Возможны 3 случая (А, Б, В на рис. 2.2).

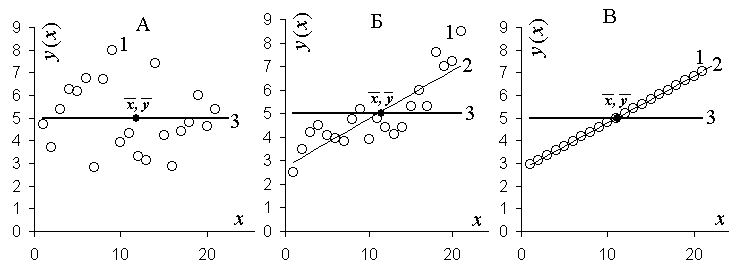
Рис. 2.2. Рассеяние переменных х и у относительно центра в случаях: А – отсутствия связи; Б – стохастической связи; В – функциональной связи (графики: 1 –значений х и у, 2 – тенденций рассеяния, 3 – средних значений у)

Графически, в системе декартовых координат, рассеяние случайных величин отображается множеством точек с общим центром . Чем хаотичнее разброс точек, чем менее оно подчинено общей тенденции, тем связь неопределеннее, то есть слабее. По смыслу неопределенность противоположна понятию реальности и силы связи, как поясняется рис. 2.2.

Рис. 2.2А отвечает рассеянию переменных х и у относительно центра при отсутствии общей тенденции группирования точек. Нельзя указать линию, проходящую через центр и отвечающую тенденции упорядочения точек, поэтому неопределенность рассеяния максимальна, связь отсутствует, задача линейной аппроксимации не имеет решения.

Рис. 2.2В отражает противоположный случай, когда нет рассеяния точек – все они строго подчиняются общей тенденции (принадлежат одной и той же прямой), то есть стохастическая связь вырождается в функциональную, и неопределенность отсутствует.

На рис 2.2Б – общий случай линейной стохастической связи, когда рассеяние точек имеет общую тенденцию, точки группируются в области, вытянутой в одном направлении, вдоль прямой, проходящей через центр и отвечающей линейной зависимости.

3. Коэффициент неопределенности, словесно определяется отношением

то есть долей рассеяния зависимой переменной у относительно модели (2.1) в общем рассеянии зависимой переменной у.

Иначе, коэффициент неопределенности – это отношение сумм квадратов:

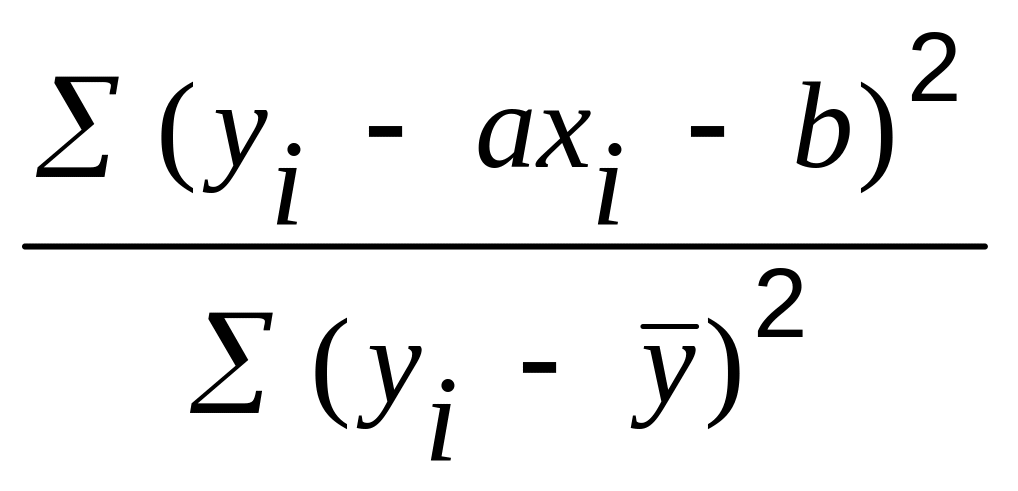. (2.6)

В числителе (2.6) – сумма квадратов разностей зависимой переменной у и модели (2.1), называемая остаточной суммой квадратов. В знаменателе – сумма квадратов отклонений y от ее среднего .

При отсутствии связи (рис. 2.2А) в группировании точек отсутствует общая тенденция, точки одинаково рассеяны относительно любой линии, проходящей через центр , в том числе линии средних значений . Поэтому отношение их рассеяний равно 1 – это максимальная величина коэффициента неопределенности.

Если точки группируются в области, вытянутой в некотором направлении, вдоль прямой, проходящей через центр и отвечающей линейной стохастической зависимости, то рассеяние y относительно нее меньше, чем относительно среднего значения (рис. 2.2Б), и коэффициент неопределенности (2.6) меньше 1.

При полном отсутствии неопределенности (рис. 2.2В) стохастическая связь вырождается в функциональную зависимость, поэтому все точки принадлежат модели (2.1), то есть относительно нее, рассеяния y нет, и коэффициент неопределенности (2.6) равен 0.

Таким образом, коэффициент неопределенности (2.6) изменяется соответственно ослаблению стохастической связи от 0 (при наиболее тесной – функциональной связи) до 1 (при отсутствии линейной связи).