3.2.7. Применение процедуры Регрессия для линейной модели
Процедура Регрессия в пакете Анализа данных выполняет методом наименьших квадратов множественную, в частности, парную линейную регрессию.
Предварительно исходные данные (массивы 1 и 2) необходимо представить в виде 2-х столбцов (столбцы В и С на рис. 3.2).
Для вызова процедуры в меню Сервис открывается пакет Анализ данных. Если в меню Сервис нет названия пакета, то возможны две причины:
1) пакет Анализ данных установлен, но не как постоянно используемый, и тогда достаточно в меню Сервис обратиться к команде Надстройки (не путать с командой Настройки!) и в ее диалоговом окне поднять флажок Анализ данных;
2) пакет Excel установлен не полностью, например, по умолчанию, и тогда потребуется переустановка пакета.
После инициализации пакета Анализ данных в его списке выбирается процедура Регрессия, выводящая диалоговое окно, где заполняются поля:
Входной интервал Y, куда вводится адрес диапазона значений зависимой переменной со строкой обозначений.
Входной интервал X, куда вводится адрес диапазона независимой переменной со строкой обозначений.
Метки, где устанавливается флажок, если первые строки входных интервалов содержат заголовки. Если флажок снят, то названия для данных создаются автоматически.
Уровень надежности, где устанавливается флажок, чтобы указать уровень надежности (по умолчанию он полагается равным 95%).
Константа – ноль, где устанавливается флажок, чтобы линия регрессии прошла через начало координат, если это априорно известно.
Выходной диапазон, куда вводится ссылка на левую верхнюю ячейку выходного диапазона – он автоматически расширяется вправо на 20 столбцов и вниз на 50 – 60 строк.
Новый лист, где устанавливается переключатель, чтобы открыть новый лист в книге и вставить результаты анализа, начиная с ячейки A1.
Новая книга, где устанавливается переключатель, чтобы открыть новую книгу и вставить результаты анализа в ячейку A1 на первом листе в этой книге.
Остатки, где устанавливается флажок для вывода остатков.
Стандартизированные остатки, где устанавливается флажок, чтобы включить стандартизированные остатки в выходной диапазон.
График остатков, где устанавливается флажок для вывода диаграммы остатков.
График подбора, где устанавливается флажок, чтобы вывести диаграмму наблюдаемых и предсказанных значений зависимой переменной, отвечающих линии регрессии.
График нормальной вероятности, где устанавливается флажок, чтобы вывести диаграмму процентелей, то есть значений случайной величины (на оси ординат), как функций накопленных эмпирических вероятностей (на оси абсцисс), что поясняется далее рис. 3.5 и комментариями к нему.
Результаты корреляционного и регрессионного анализов выводятся в таблицах с шапками и боковиками, отражающими содержание данных.
Таблица Regression Statistics представлена ниже (таблица 3.2).
Таблица 3.2
Статистики регрессии
Regression Statistics |
|
Multiple R |
0,9613595 |
R Square |
0,9242121 |
Adjusted R Square |
0,9178964 |
Standard Error |
3,7989243 |
Observations |
14 |
В таблице 3.2 выведены (сверху вниз):
– Multiple R – коэффициент множественной корреляции (в случае парной линейной связи – просто коэффициент корреляции);
– R Square – квадрат коэффициента корреляции;
– Adjusted R Square – это Adjusted R2 (2.38), (2.39);
– Standard Error – стандарт рассеяния зависимой переменной y относительно регрессии (S2);
– Observations – объем выборки (n).
Таблица ANOVA (сокращение Analysis of Variance – дисперсионного анализа) представлена ниже (таблица 3.3).
В строке Regression (рассеяние отклонений зависимой переменной в модели) указаны слева направо:
– df – число степеней свободы (для рассеяния в модели 1 степень модели);
– SS – сумма квадратов отклонений значений модели от среднего;
– MS – дисперсия отклонений значений модели от среднего (поскольку df = 1, совпадает с SS) – рассматривалась как D1 (2.33);
– F – отношение дисперсий, которое входит в выражение (3.3);
– Significance F – доверительная вероятность ошибки того, что F 1, то есть отклонения нулевой гипотезы, практически равна нулю.
Таблица 3.3
Анализ дисперсий
ANOVA |
|
|
|
|
|
|
df |
SS |
MS |
F |
Significance F |
Regression |
1 |
2111,903977 |
2111,904 |
146,336577 |
4,42093E-08 |
Residual |
12 |
173,1819084 |
14,43183 |
|
|
Total |
13 |
2285,085886 |
|
|
|
В строке Residual (рассеяние остатков) указаны слева направо:
– df – число степеней свободы (при линейной связи n – 2);
– SS – сумма квадратов остатков;
– MS – дисперсия остатков, которая рассматривалась, как D2 (2.35).
В строке Total (общее рассеяние зависимой перемеренной относительно среднего):
– df – число степеней свободы – с учетом одной связи (среднего) n – 1;
– SS – сумма квадратов отклонений зависимой перемеренной относительно среднего (складывается из рассеяния зависимой перемеренной в модели и относительно модели).
Таблица с коэффициентами регрессии и их доверительными интервалами выводится без названия ниже таблицы ANOVA, имея содержание, показанное в таблице 3.4.
Таблица 3.4
Статистики коэффициентов регрессии
|
Coefficients |
Standard Error |
t Stat |
P-value |
Lower 95% |
Upper 95% |
Intercept |
-8,20314 |
2,143046 |
-3,8278 |
0,002405 |
-12,87244 |
-3,533847 |
X Variable 1 |
0,62918 |
0,052011 |
12,09697 |
4,42E-08 |
0,515858 |
0,742504 |
В строке Intercept – данные о свободном члене уравнения (3.2).
Строка X Variable 1 содержит оценки коэффициента при независимой переменной (для парной линейной связи она единственная и первая).
В столбце Coefficients – указаны значения параметров линейной связи (свободного члена и коэффициента при независимой переменной), которые, естественно, совпадают с вычисляемыми другими средствами.
В столбце Standard Error приведены среднеквадратичные погрешности оценок параметров линейной связи, которые также совпадают с полученными другими средствами.
В столбце t Stat находятся нормированные значения параметров – частные от деления оценок Coefficients на оценки Standard Error.
Смысл t Stat состоит в оценке значимости t-отклонений параметров от нуля с помощью распределения Стьюдента: чем больше t-отклонение, тем меньше вероятность ошибки отклонения нулевой гипотезы о равенстве параметра нулю.
В столбце P-value – вероятности ошибки отклонения нулевой гипотезы о равенстве параметра нулю (они намного меньше обычной критической величины 0,05).
В столбцах Lower 95% и Upper 95% – наименьшие и наибольшие допустимые границы колебаний оценок параметров с вероятностью до 95%. Граничное значение подсчитывается следующим образом:
– встроенная функция =СТЬЮДРАСПОБР(0,05;12) = 2,1788 возвращает критическое значение t-отклонения с вероятностью не менее 5% при 12 степенях свободы;
– для перехода к натуральному (ненормализованному) критическому значению параметра, найденное t-отклонение умножается на стандарт оценки параметра в столбце Standard Error, в частности, для параметра Intercept получается 2,1788 2,1430 = 4,6693;
– граничные значения подсчитываются с учетом величины параметра в столбце Coefficients: -8,2031 – 4,6693 = -12,8724 и -8,2031 + 4,6693 = -3,5338.
Таблица RESIDUAL OUTPUT (вывод остатков) состоит из 4 столбцов (табл. 3.5).
Таблица 3.5
Остатки регрессии
RESIDUAL OUTPUT |
|
|
|
Observation |
Predicted y |
Residuals |
Standard Residuals |
1 |
43,3897087 |
6,610291345 |
1,811094104 |
2 |
37,0978974 |
-2,197897386 |
-0,602182081 |
3 |
24,5142749 |
0,48572515 |
0,133079453 |
4 |
17,5932825 |
-5,593282455 |
-1,532453011 |
5 |
15,7057391 |
-0,705739075 |
-0,193359084 |
6 |
15,0765579 |
-2,076557948 |
-0,568937383 |
7 |
11,9306523 |
-4,950652314 |
-1,356384575 |
8 |
11,3014712 |
-1,301471187 |
-0,356578352 |
9 |
9,41392781 |
-3,423927806 |
-0,938091098 |
10 |
6,8972033 |
2,082796701 |
0,570646682 |
11 |
5,63884105 |
1,341158955 |
0,367452045 |
12 |
4,38047879 |
0,609521208 |
0,166997218 |
13 |
2,49293541 |
3,487064589 |
0,955389375 |
14 |
-0,6529702 |
5,632970223 |
1,543326705 |
В столбце Observation – номера по порядку исходных данных.
В столбце Predicted y – прогнозируемые (вычисленные по уравнению линейной регрессии) значения зависимой переменной y.
В столбце Residuals – остатки (разности фактических и прогнозируемых значений зависимой переменной y).
В столбце Standard Residuals – нормализованные значения остатков (значения столбца Residuals, поделенные на стандарт остатков). Он определяется из дисперсии (таблица 3.3), вычисленной с n – 2 степенями свободы, но стандарт подсчитан неверно с числом степеней свободы n – 1, вместо n – 2, и значения столбца Standard Residuals несколько завышены.
Таблица PROBABILITY OUTPUT (вывод вероятностей) состоит из процентилей исходных значений зависимой переменной y, как показано в таблице 3.6.
Таблица 3.6
Процентили значений зависимой переменной y
PROBABILITY OUTPUT |
|
Percentile |
y |
3,571428571 |
4,98 |
10,71428571 |
4,99 |
17,85714286 |
5,98 |
25 |
5,99 |
32,14285714 |
6,98 |
39,28571429 |
6,98 |
46,42857143 |
8,98 |
53,57142857 |
10 |
60,71428571 |
12 |
67,85714286 |
13 |
75 |
15 |
82,14285714 |
25 |
89,28571429 |
34,9 |
96,42857143 |
50 |
Процентили – это случайные величины, отвечающие данным вероятностям в %.
Иначе, процентили – это абсциссы интегральной кривой (рис. 3.5). Если вероятность выражена в долях единицы, то абсциссы интегральной кривой называются квантилями.
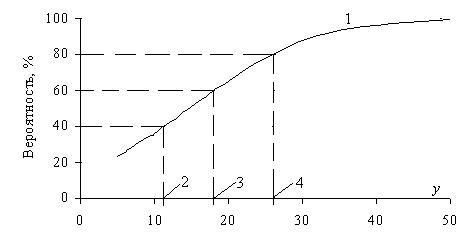
Рис. 3.5. Интегральная кривая (1) и процентили с уровнями вероятностей: 40% (2), 60% (3) и 80% (4)
В столбце Percentile (таблица 3.6) приведены не процентили и не квантили, а вероятности в %, то есть не абсциссы, а ординаты (рис.3.5), вместо интегральных, взяты накопительные вероятности зависимой переменной y. Все значения y упорядочивались по возрастанию и оценивались их процентные доли, исходя из следующего:
– между 14 значениями y имеется 13 интервалов, к которым добавляется еще две половины интервала (к первому и последнему значениям) – всего 14;
– на шкале вероятностей (от 0 до 100%) на 1 интервал приходится 100% / 14 = 7,14%;
– на шкале вероятностей положению первого значения y (4,98) отвечает конец полуинтервала, то есть 7,14% / 2 = 3,57%;
– положение на шкале вероятностей 2-го значения y (4,99) определяется добавлением интервала 3,57%+7,14% = 10,71%, вероятность 3-го значения 10,71% + 7,14% = 17,85% и т.д.;
– последнее значение y (50) не достигает конца (100% ) – находится в полуинтервале от конца 100% – 3,57% =96,43%.