2.4.4. Оценка адекватности линейной модели
Качество линейной модели, то есть ее соответствие, пусть неизвестной, но объективно существующей истинной зависимости предполагает адекватность математических свойств модели и исходных данных.
1. Поведение и области определения переменных и производных модели должны соответствовать сущности искомой зависимости.
Необходимость соблюдения этого требования поясняется примером (рис. 2.7) линейной регрессии цен вин на годы их выдержки, которая, хотя и характеризуется значимым коэффициентом корреляции (0,961), не адекватна сущности зависимости, поскольку:
– области определения переменных модели не ограничены, тогда как годы выдержки вина и цены, естественно, не могут быть отрицательными;
– производная модели положительна и постоянна (график имеет постоянный угол наклона), а фактическиt приращения цен монотонно убывают с уменьшением выдержки и асимптотически приближаются нулю;
– свободный член модели (отрезок, отсекаемый на оси ординат) значим и отрицателен, что противоречит смыслу цены вина.
2. Статистическое распределение остатков модели должно соответствовать рассеянию случайной составляющей исходных данных.
Остатки (residuals) являются разностями фактических и аппроксимирующих значений зависимой переменной.
В идеале, когда модель адекватна исследуемому явлению, остатки отвечают случайной составляющей зависимой переменной (являются латентными). Дисперсия D2 остатков (2.34) при этом рассматривается как оценка дисперсии случайной составляющей.
Соответствие остатков свойствам и характеру случайной составляющей (погрешностям) зависимой переменной – необходимый критерий адекватности модели исследуемому явлению, выполнение которого проверяется:
– отсутствием статистически значимых расхождений дисперсий остатков и исходных данных по критерию Фишера для отношения этих дисперсий;
– согласием статистического распределения остатков с законом (обычно нормальным) распределения случайной составляющей исходных данных.
3. Отсутствие нелинейного компонента в последовательности остатков линейной аппроксимации – условие линейности искомой истинной зависимости эмпирических данных, то есть адекватности модели.
Последовательность остатков должна иметь случайный характер, когда между значениями остатков отсутствует корреляционная связь – так называемая автокорреляция.
Так, например, остатки линейной зависимости, показанной на рис. 2.07, образуют неслучайную последовательность, которая (рис. 2.08), приближенно описывается параболой с квадратом корреляционного отношения 0,66 и самим корреляционным отношением 0,82.
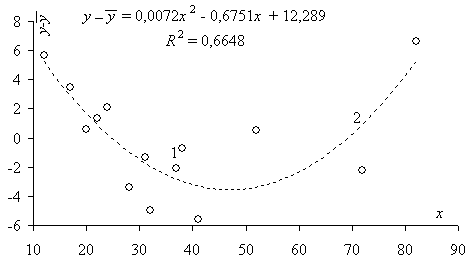
Рис. 2.08. Графики остатков: 1 – фактические; 2 –приближения параболой
Очевидно, в данном случае линейная модель не адекватна истинной зависимости, то есть линейная аппроксимация формально допустима, однако не является оптимальной, так как не адекватна рассматриваемым связям, приводит к некорректной области определения переменных и игнорированию нелинейной составляющей зависимости, что снижает качество моделирования и его разрешающие возможности, в частности:
– уменьшается точность прогнозных оценок;
– сужается область корректного моделирования зависимости, даже в интервале заданных значений выдержки;
– слишком упрощенная аппроксимация не позволяет раскрыть особенности зависимости и правильно проинтерпретировать их.