2.2.3.Ёмкость (с)

Рис.2.15. Условно-положительные направления тока и напряжения на емкости

Пусть через емкость протекает синусоидальный ток

i = I_msint.

По определению , где q – заряд.

Для емкости

q = CU. 26(2.22)

Для линейного конденсатора C = const, поэтому

i = , 27(2.23)

откуда

где X_C = .

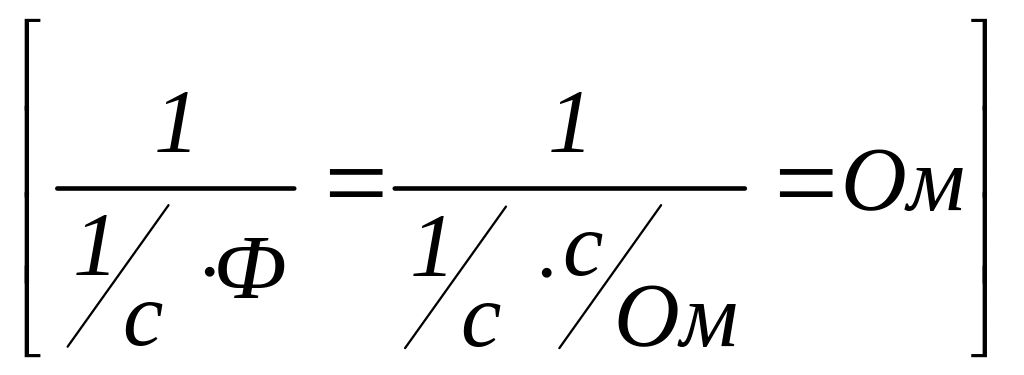Ток в ёмкости опережает приложенное напряжение на угол 90⁰, также можно считать, что напряжение отстаёт от тока на 90⁰.

Определим мгновенную мощность

p = ui = UIsin2t. 28(2.24)

Среднее значение мощности за период

. 29(2.25)

Таким образом, идеальная емкость не потребляет из сети мощность. Для оценки запасенной в емкости энергии электрического поля вводят понятие реактивной мощности, равной

, [вар]. 30(2.26)

График функции мгновенной мощности представлен на Рис. 2 .16. Где p > 0, энергия идёт на создание электрического поля, где p < 0, происходит возврат энергии.

Рис.2.16. Графики мгновенных значений тока, напряжения и мощности на емкости

2.3.Изображение синусоидальных функций времени (напряжение, сила тока, мощность) векторами на комплексной плоскости

Расчет сложной разветвленной цепи может быть существенно упрощен, если заменить синусоидальные токи и напряжения векторами, расположенными на комплексной плоскости. Такой метод получил название метода комплексных амплитуд.

В основе данного метода лежит формула Эйлера

, 31(2.27)

где j = .

Умножив обе части на А, получим

A = A₁+jA₂,

где A =  модуль комплексного числа;

 аргумент комплексного числа.

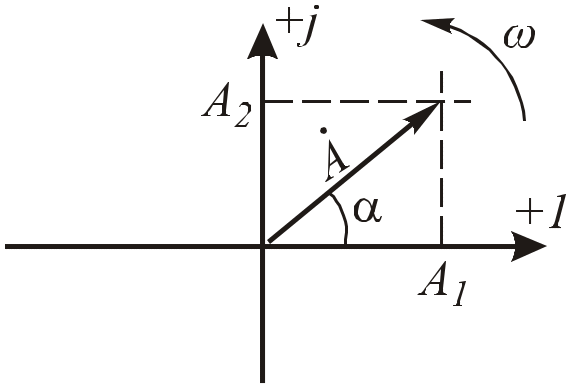
Рис.2.17. Изображение вектора на комплексной плоскости

(  угловая частота вращения вектора )

Поскольку в формуле Эйлера  может быть любым, мы сделаем его линейной функцией времени

 = t + . 32(2.28)

Тогда

. 33(2.29)

Полученный результат ( 2 .30) показывает, что синусоидальная функция времени есть мнимая часть некоторого комплексного числа

а = Asin(t +) = I_mAe^j(t+); 34(2.30)

при условии, что t = 0 получим

 = A . 35(2.31)

Векторная диаграмма  диаграмма векторов на комплексной плоскости, построенная с учетом их взаимной ориентации по фазе.

Если вектора вращаются на плоскости с одинаковыми частотами , то их взаимное положение не меняется, это свойство позволяет исключить из рассмотрения сам факт их вращения, то есть принимать t = 0.

В качестве примера на рис.2.10 изображена операция умножения некоторого вектора на оператор поворота j.

Пусть модуль = 10А. Его положение на комплексной плоскости зависит от значения аргумента. Значениям  = 0, 90⁰,  90⁰ соответствуют комплексные числа :

; ; .

По формуле Эйлера

;

;

;

;

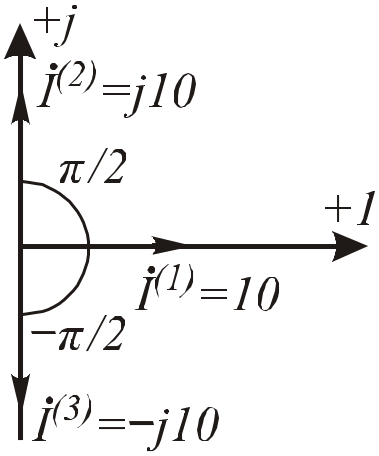
Рис.2.18. Умножение вектора на +j и –j