7.5.Несинусоидальные функции времени с периодической огибающей
В отличие от периодических функций, рассмотренных выше, существуют несинусоидальные кривые с периодическими или почти периодическими огибающими. Для них характерно то, что они имеют конечное число слагаемых в разложении. Причем частоты огибающих и составляющих ряда несоизмеримы. Классическими примерами таких функций являются биения и модуляция.
7.5.1.Биения
Функция биения представляет собой сумму двух синусоидальных колебаний, имеющих одинаковые амплитуды и близкие, но не равные частоты.
f1 = Amsinω1t, f2 = Amsinω2t, причем ω1 > ω2, ω1 ≈ ω2.
Сумма этих функций
.
Обозначим
;
.
Тогда
;
ω >> Ω.
Рис.7.105. График функции биения
Из рис. 7.4 следует, что частота огибающей или частота биений fб = / равняется числу максимумов огибающей кривой в единицу времени.
Период биений Тб не равен периоду кривой f(t):
;
Если отношение / = 2k – 1 составляет целое нечетное число, то период биений совпадает с периодом кривой f(t).
В случае, когда период биений и период огибающей несоизмеримы, т.е. их отношение не равно целому числу, результирующее колебание является квазипериодическим.
7.5.2.Модуляция
Синусоидальные колебания характеризуются тремя основными параметрами: амплитудой, частотой и начальной фазой. В случае, когда один из этих параметров медленно меняется во времени по некоторому периодическому закону, то говорят об амплитудной, частотной или фазовой модуляции. Рассмотрим данное явление на примере амплитудной модуляции, которая может быть представлена функцией вида
f(t) = Am(t)sinωоt,
где Am(t) – меняется по некоторому периодическому закону.
f(t) = Aоm(1 + mcosΩt)sinωоt; ωо >> Ω
ωо – несущая частота;
Ω – модулирующая частота;
m < 1 – коэффициент(глубина) модуляции. Он показывает отклонение амплитуды модулирующего колебания от некоторого среднего значения.
f(t) = Aоmsinωоt + Aоmmcos(Ωt)sinωоt;.
f(t) = Aоmsinωоt + 0,5Aоmm·[sin(ωо – Ω)t + sin(ωо+Ω)t].
В результате модулированные по амплитуде колебания являются суммой трех колебательных составляющих. Одно происходит с несущей частотой ωо. Два других – с боковыми частотами (ωо – Ω ) и (ωо + Ω ). Сказанное позволяет построить результирующую функцию, приведенную на рис. 7.5.
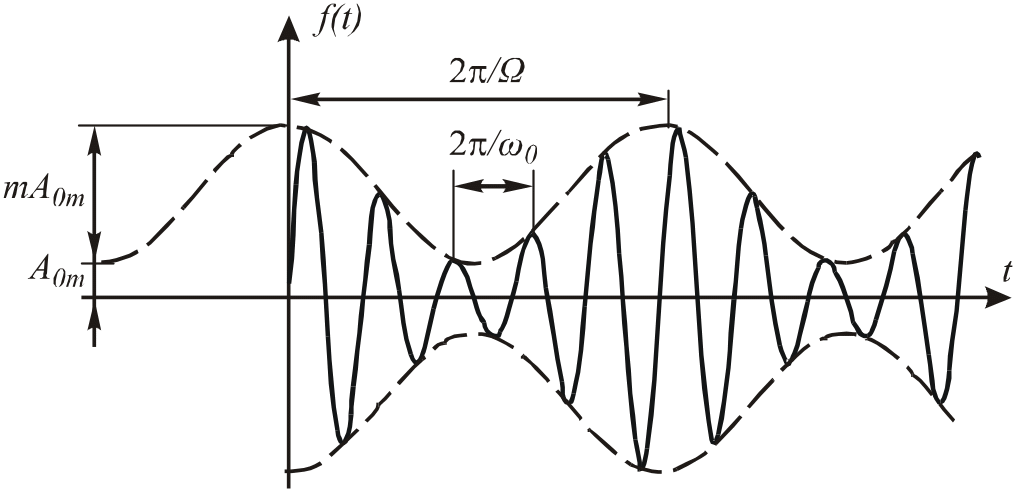
Рис.7.106. График модулированных по амплитуде колебаний
Этот вид модуляции далеко не лучший, поскольку он в наибольшей степени подвержен помехам. Для повышения помехоустойчивости используются комбинированные методы модуляции.
7.6.Резонансные явления в цепях с несинусоидальными источниками
Рассматривая однофазные синусоидальные цепи, мы познакомились с явлением резонанса. Указанные явления имеют место в цепях и с несинусоидальными источниками, однако, в этом случае они имеют определенную специфику, связанную с тем обстоятельством, что резонанс может возникнуть как на основной, так и на высших гармониках.
Для последовательного контура в цепях с несинусоидальным источником условие резонанса будет задано соотношением
,
где ω - частота основной гармоники; k – номер гармоники.
На рис. 7.6 приведена зависимость, иллюстрирующая данное явление.
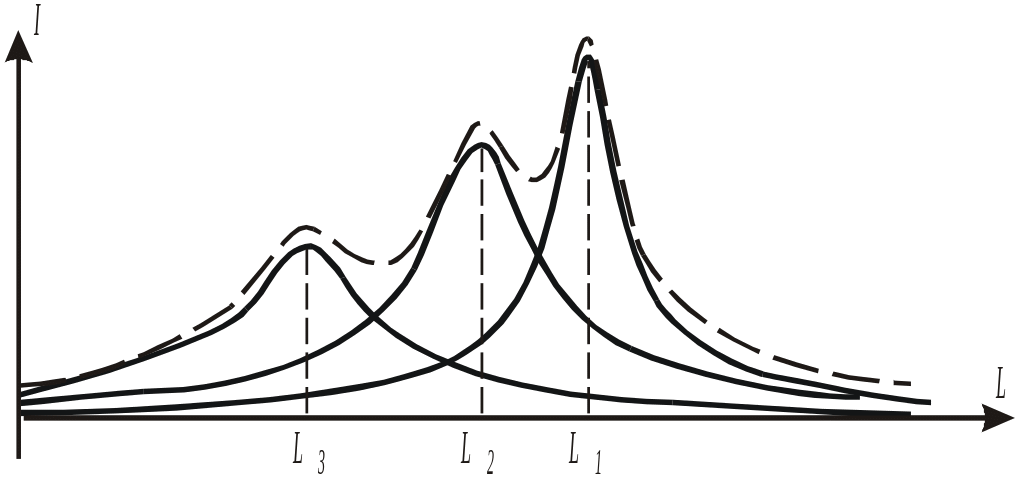
Рис.7.107. Зависимость тока от индуктивности
.