6.2.8.Вносимое сопротивление трансформатора

Пусть к выходным зажимам трансформатора по рис. 6.17 подключен приемник с сопротивлением Z_н.

Z_н = R_н + jX_н .

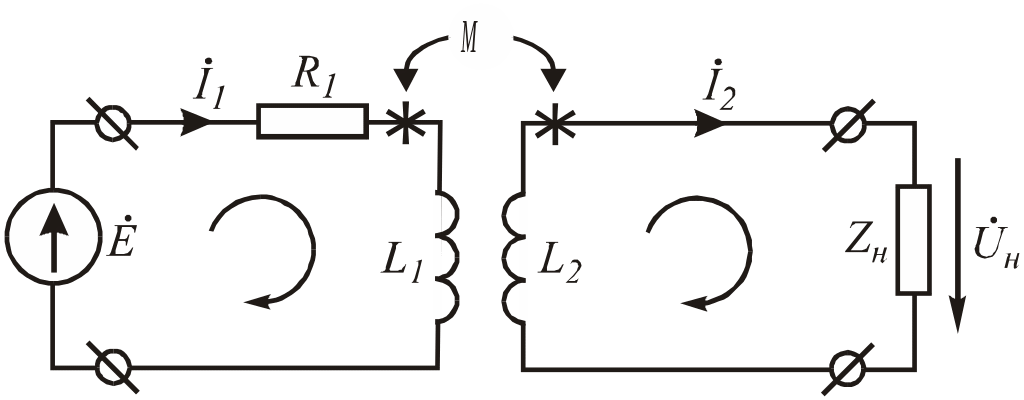
Рис.6.100. Схема нагруженного трансформатора

Вновь составим систему уравнений для данной цепи по законам Кирхгофа с учетом выбранного направления обхода.

133(6.135)

Выразим из второго уравнения ток и подставим его в первое уравнение. Так как , то получим следующее выражение для тока :

.

Подставляя его в первое уравнение, получим

; 134(6.136)

.

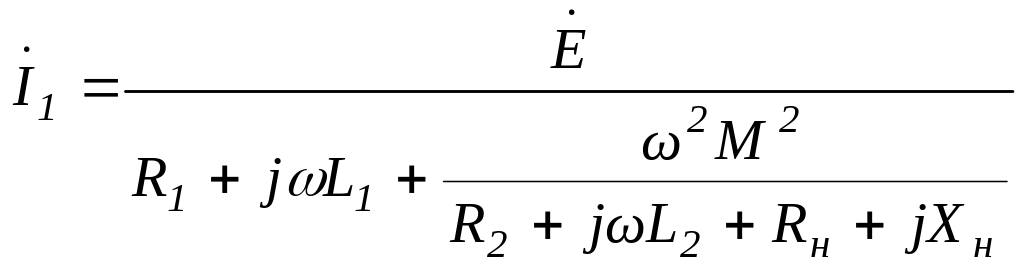Проведя ряд алгебраических преобразований, получим следующее выражение для тока

.

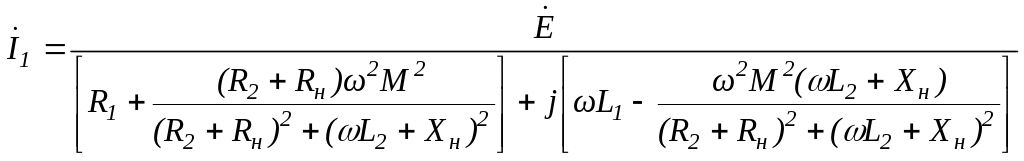Обозначим

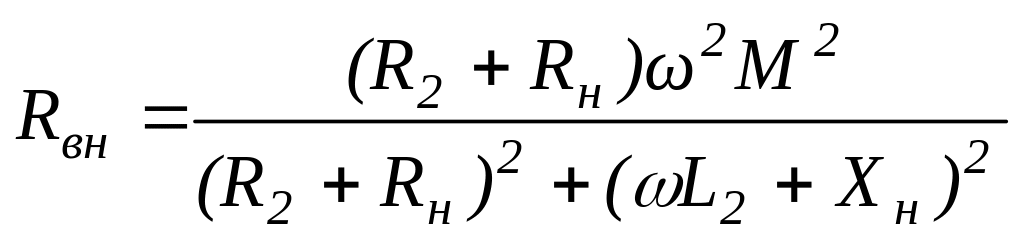, 135(6.137)

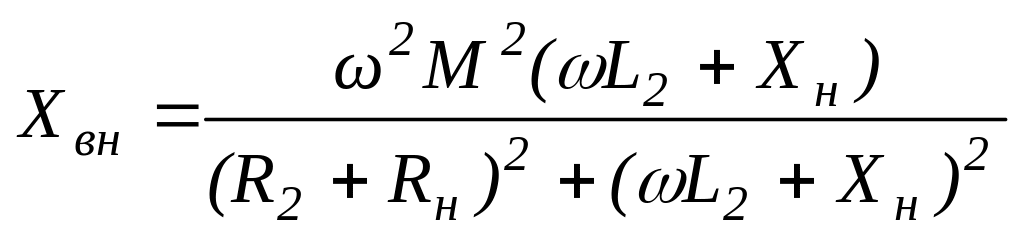, 136(6.138)

где R_вн и X_вн – соответственно активное и реактивное вносимые сопротивления трансформатора.

Тогда окончательно имеем

. 137(6.139)

Физически вносимое сопротивление представляет собой такое сопротивление, включенное последовательно с первичной обмоткой, которое позволяет учесть влияние тока нагрузки на ток .

Построим векторную диаграмму трансформатора под нагрузкой.

Пусть в качестве нагрузки используется активно-индуктивный потребитель (_н > 0). Для построения диаграммы используем составленную выше систему уравнений ( 6 .135). Построение векторной диаграммы, приведенной на рис. 6.18, целесообразно начать с тока , совместив его для определенности с осью вещественных чисел.

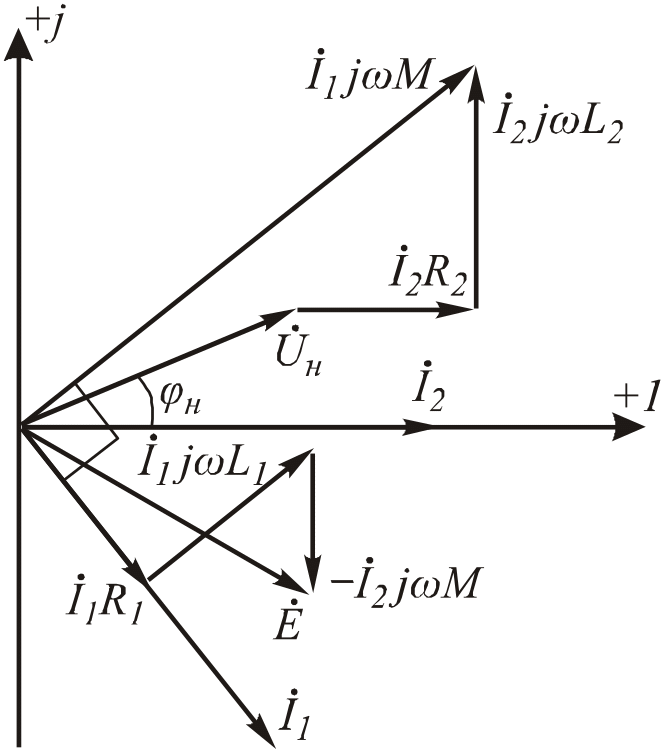
Рис.6.101.Векторная диаграмма трансформатора под нагрузкой

7.Несинусоидальные токи

Расчет электрических цепей, выполненный ранее, проводился в предположении, что источники энергии были либо постоянными, либо синусоидальными и вызывали в элементах цепей постоянные или синусоидальные токи. В реальных условиях кривые ЭДС, напряжения и тока лишь в определенной мере могут считаться синусоидальными, при этом указанные параметры цепей могут иметь характер периодический, квазипериодический (почти периодический) и непериодический. Это происходит за счет наличия в электрических цепях нелинейных элементов: вентиль (диод), электрическая дуга, катушка со стальным сердечником (дроссель), различного рода электрические помехи и т.д., которые искажают синусоидальную функцию, приводя к появлению несинусоидальных функций токов и напряжений, кроме того, сам источник энергии может являться генератором несинусоидальной ЭДС. На рис. 7.1 представлены варианты данных функций.

Рис.7.102. Пример несинусоидальных периодических функций

7.1.Разложение периодической функции в тригонометрический ряд

Во всех задачах, где приходится иметь дело с периодическими несинусоидальными функциями токов, ЭДС и напряжений, необходимо свести их к более простому виду, для которого возможно применение известных методов расчета. Процессы, происходящие в линейных электрических цепях при несинусоидальных токах и напряжениях, удобнее всего рассчитывать, если воспользоваться тригонометрическим рядом Фурье. В общем случае выражение этого ряда имеет вид

f(ωt) = A₀ + A_1msin(ωt+ψ₁) + A_2msin(2ωt + ψ₂) + … 138(7.140)

Первое слагаемое носит название нулевой гармоники или постоянной составляющей ряда, где k  номер гармоники, при k = 0 ψ_k = π/2, A_km = A₀  нулевая гармоника. Она присутствует в составе ряда не всегда. Если функция симметрична относительно оси времени, то нулевой гармоники нет.

Второе слагаемое  это первая или основная гармоника ряда, задает основной период T = 2π/ω.

Все остальные слагаемые носят название высших гармоник ряда. Период каждой из них кратен периоду основной гармоники. Сделаем преобразование ряда, раскрыв синус суммы,

. 139(7.141)

; ;

; .

Коэффициенты ряда определяются по следующим формулам:

; 140(7.142)

;

.

Выражения для коэффициентов ряда позволяют получить разложение в ряд любой периодической функции, однако для большинства таких функций, которые используются в теории электрических цепей, эти разложения уже получены и могут быть взяты в соответствующей справочной литературе.

Состав элементов ряда может быть упрощен, если вид исходной функции обладает тем или иным видом симметрии, что иллюстрируется рис. 7.2.

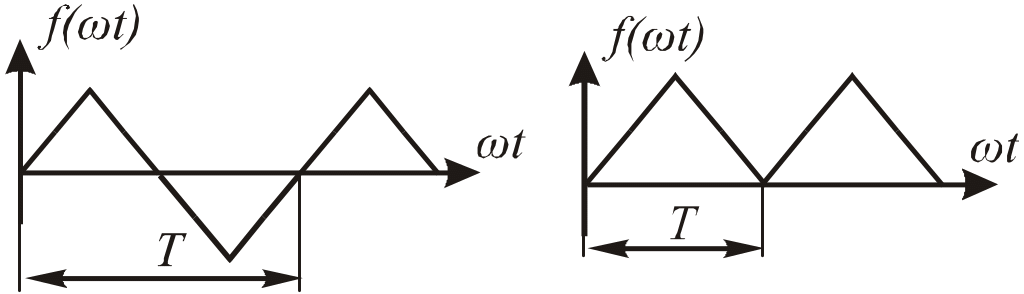
Рис.7.103. Виды симметрии периодических функций

1) f(ωt) =  f(ωt+π) – функция симметричная относительно оси абсцисс.

Разложение в ряд такой функции не содержит постоянной составляющей и четных гармоник:

f(ωt) = A_1msin(ωt + ψ₁) + A_3msin(3ωt + ψ₃) + A_5msin(5ωt + ψ₅) + …

2) f(ωt) = f( ωt) – функция симметричная относительно оси ординат.

В этом случае ряд не содержит синусных составляющих:

f(ωt) = A₀ + A_1mcosωt + A_2mcos2ωt + A_3mcos3ωt + …

3) Функция симметрична относительно начала координат:

f(ωt) =  f(ωt);

Такая функция не содержит постоянной составляющей и косинусных составляющих:

f(ωt) = A_1msinωt + A_2msin2ωt + A_3msin3ωt + …