1.6. Квадратичне наближення лінійною функцією

Як інтерполяційний поліном беремо поліном першого степеня (n=1): y_L = S₁(x) = a₁₁x + a₀₁.

Коефіцієнти a₁₁ та a₀₁ треба визначити з умови мінімізації квадратичного відхилення

Δy_Li = y_L(x_i) – y_i = a₁₁x_i + a₀₁ – y_i. (1.15)

Квадратичне зважування запишемо у вигляді

F₁(a₁₁, a₀₁) → min. (1.16)

Необхідна умова мінімуму дає систему

; ; (1.17)

; .

Одержали систему двох алгебраїчних рівнянь відносно двох невідомих a₁₁ та a₀₁. Введемо позначення, розділивши обидва рівняння системи (1.17) на N.

= ; = ; = ; = . (1.18)

З врахуванням позначень зведемо (1.17) до канонічного вигляду

,

(1.19)

Знайдемо значення a₁₁ та a₀₁ за формулами

; , (1.20)

де визначники

; ; . (1.21)

Згідно з (1.19) повинна виконуватись умова

, (1.22)

яка може служити перевіркою розрахунків.

М

Інтерполяція функцій методом найменших квадратів

інімальне середньоквадратичне відхилення

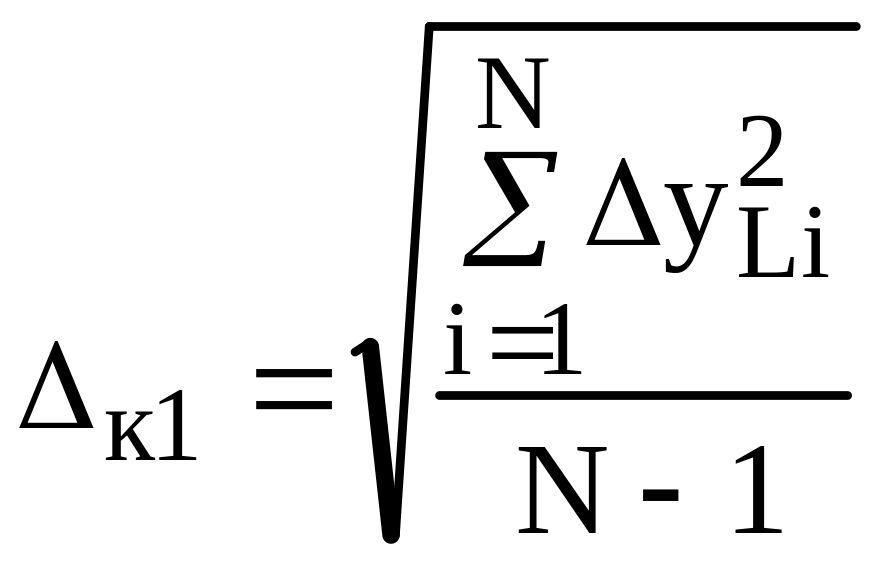. (1.23)

1.7. Квадратичне наближення квадратним тричленом

Інтерполяція здійснюється з допомогою тричлена другого степеня

y_K = a₂₂x² + a₁₂x + a₀₂. (1.24)

Похибки у вузлах визначаються формулою

Δy_Ki = y_K(x_i) – y_i = a₂₂x² + a₁₂x + a₀₂ – y_i. (1.25)

Середньоквадратичне відхилення у вузлах описується залежністю

= F₂(a₂₂, a₁₂, a₀₂). (1.26)

Мінімізуємо (1.26) і отримаємо

, ;

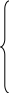, ; (1.27)

, .

Введемо ще такі позначення:

= ; = ; = . (1.28)

Одержимо систему трьох алгебраїчних рівнянь із трьома невідомими a₂₂, a₁₂, a₀₂

(1.29)

,

яку розв’яжемо за допомогою визначників:

; ;

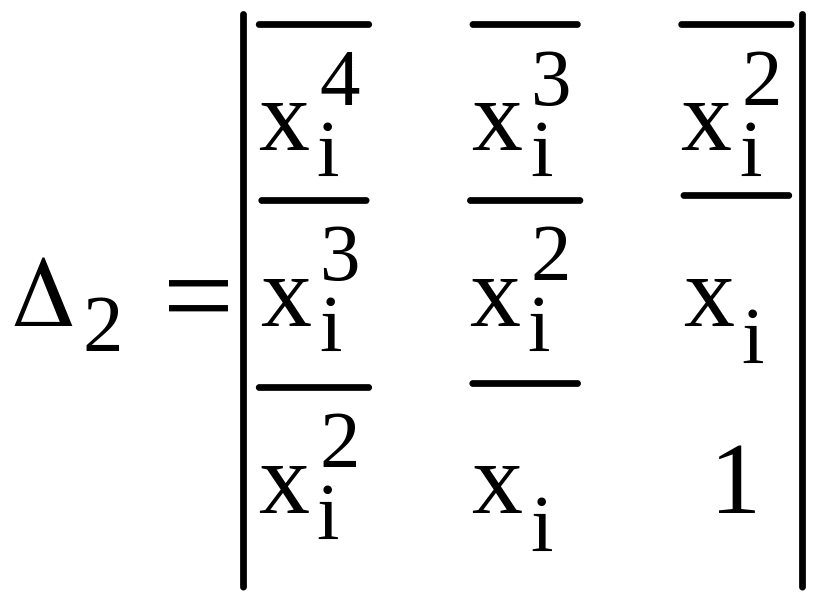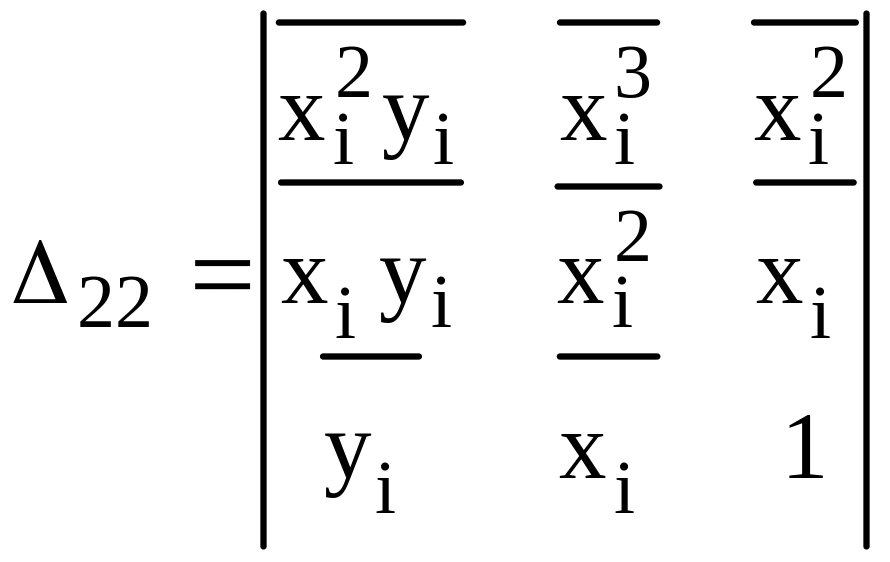Робота №1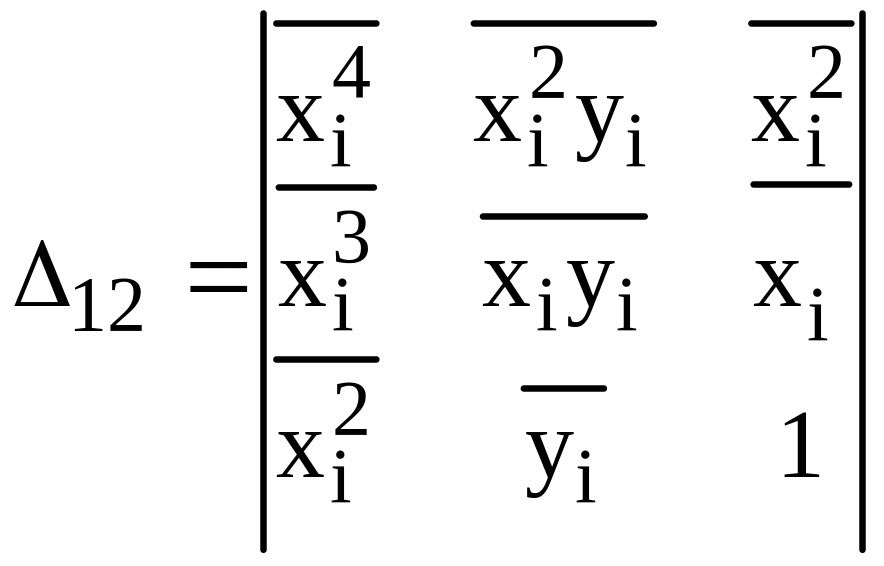

; . (1.30)

Коефіцієнти тричлена визначаються за формулами:

; ; . (1.31)

Для перевірки розрахунків використаємо умову

.

Мінімальне середньоквадратичне відхилення

. (1.32)

2. Індивідуальне завдання

1. Для заданої таблиці експериментальних даних (табл. 1.2) методом квадратичного наближення визначити: інтерполяційну лінійну функцію , відповідне середньоквадратичне відхилення, максимальне відхилення у вузлах.

2. Для таблиці експериментальних даних методом квадратичного наближення визначити інтерполяційний квадратичний тричлен та визначити відповідне середньоквадратичне відхилення та максимальне відхилення у вузлах.

3. Порівняти середньоквадратичні відхилення та максимальні відхилення у вузлах обох наближень та зробити висновки.

3. Порядок виконання роботи

1. Розрахувати квадратичне наближення лінійною функцією, заповнити відповідні стовпці таблиці 1.3.

2. Розрахувати квадратичне наближення квадратичним тричленом, заповнити стовпці таблиці 1.3.

3. Знайти середньоквадратичне відхилення та максимальні відхилення у вузлах при розрахунку лінійної функції та при розрахунку квадратного тричлена. Зробити висновки.

4. Побудувати графіки функцій y_L, y_K та зобразити інтерполяційні вузли (x_i, y_i)

Т

Інтерполяція функцій методом найменших квадратів

аблиця 1.2