Структурные средние величины

Наиболее часто применяемыми структурными средними величинами являются: мода, медиана, квартили, децили, перцентили.

Все структурные средние являются именованными величинами.

Мода ( ) – величина признака (варианту), которая наиболее часто встречается в исходной совокупности.

В дискретном вариационном ряду модой является варианта, имеющая наибольшую частоту (частость).

Пример 5. Используя распределение 25 работников по тарифному разряду (цифры условные) рассчитать моду.

Тарифный разряд,	Число работников, чел.,
1	3
2	5
3	4
4	6
5	3
6	4
Итого	25

Решение. В данном примере наибольшей частоте (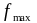 = 6) соответствует величина признака, равная 4. Значит, = 4 тарифному разряду, т. е. наиболее часто в исходной совокупности встречаются работники, имеющие четвертый тарифный разряд.

В интервальном вариационном ряду с равными интервалами моду рассчитывают по формуле

,

где – нижняя граница интервала, содержащего моду;

– величина модального интервала;

– частота (частость) модального интервала;

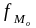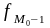– частота (частость) интервала, предшествующего

модальному;

– частота (частость) интервала, следующего за модальным.

Пример 6. По приведенным условным данным о трудовом стаже 20 работников отдела вычислить моду (по формулам и графически).

Стаж работы работников, лет	Численность работников, чел.
до 5	2
5 –10	3
10–15	10
15–20	5
Итого	20

Решение. По наибольшей частоте ( = 10) определяем, что модальным является интервал по стажу работы 10–15 лет. Подставим значения в формулу и вычислим моду

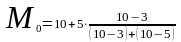= 12,9 лет,

т. е. чаще встречаются работники, имеющие трудовой стаж примерно 13 лет.

В интервальном вариационном ряду моду можно вычислить графически по гистограмме (рис. 4).

Рис. 4. Гистограмма

В интервальном вариационном ряду с неравными интервалами моду рассчитывают по формуле

,

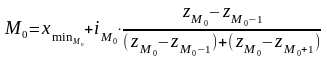где z – плотности распределения = .

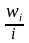Пример 7. По приведенным условным данным вычислить моду

Размер заработной платы, руб. / мес.	Численность работников, чел.
до 5000	4
5 000–7 000	12
7 000–10 000	8
10 000–15 000	6
Итого	30

Решение. В данном вариационном ряду интервалы группировки неравные, все предварительные расчеты представим в таблице:

		=		=
1	2	3	4	5
до 5 000	4	13	2 000	0,0065
5 000–7 000	12	40	2 000	0,0200
7 000–10 000	8	27	3 000	0,0090
10 000–15 000	6	20	5 000	0,0040
Итого	30	100

Наибольшая плотность распределения = 0,020.

Это означает, что модальным является интервал 5 000 – 7 000 руб.

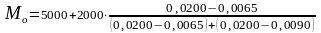= 6 102 (руб.),

т. е. большинство сотрудников получают заработную плату в размере 6 102 руб. в месяц.

В интервальном вариационном ряду с неравными интервалами моду также можно вычислить графически по гистограмме (по аналогии с ее определением в интервальном вариационном ряду с равными интервалами, только по оси ординат вместо частот (частостей) откладывают соответствующие плотности распределения).

Медиана ( ) – значение признака (варианта), которое имеет единица совокупности, делящая исходную совокупность на две равные по числу единиц части, т. е. в соотношении : .

Квартиль (Q) – значение признака, которое делит исходную совокупность на 4 равные по числу единиц части. Например, при вычислении первого квартиля ( ) исходная совокупность делится в соотношении 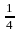: , третьего ( ) – в соотношении : .

Д ециль (D) – значение признака, который делит исходную совокупность на 10 равных частей. Например, при вычислении первого дециля (

) исходная совокупность делится в соотношении 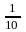: 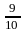, а при вычислении девятого дециля ( ) исходная совокупность делится в соотношении : .

В дискретном вариационном ряду значениями медианы, квартилей и децилей являются варианты, соответствующие единицам совокупности, которые делят исходную совокупность в нужном соотношении.

Пример 8. По исходным данным примера 5 рассчитать медиану, третий квартиль и девятый дециль.

Решение. Вычислим накопленные частоты и определим порядковые номера соответствующих единиц совокупности.

		S
1	3	3
2	5	8
3	4	12
4	6	18
5	3	21
6	4	25
Итого	25	–

= 12,5 единица;

= 18,75 единица;