Изучение степени тесноты связи между качественными признаками
Для определения
тесноты связи двух качественных
признаков, каждый из которых состоит
только из двух групп, применяются
коэффициенты ассоциации
(
)
и контингенции
(
).
Для их вычисления строится таблица, показывающая связь между двумя явлениями, каждое из которых должно быть альтернативным:
а |
b |
с |
d |
Коэффициенты вычисляются по формулам
ассоциации:
=
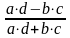
контингенции:
=
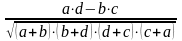
Связь между двумя качественными признаками считается подтвержденной, если > 0,5 или > 0,3.
.Пример 3. Определить степень тесноты связи между успеваемостью студентов по математике и посещением занятий по этой же дисциплине.
Группы студентов |
Численность студентов –всего, чел. |
Из них |
|
Успешно сдали экзамен |
Не сдали экзамен |
||
Посещающие занятия |
19 |
16 |
3 |
Не посещающие занятия |
7 |
2 |
5 |
Решение. Рассчитаем коэффициенты ассоциации и контин-генции
=
=
=
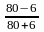= 0,86;
=
= =
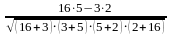= 0,53.
Значения полученных
коэффициентов ассоциации и контингенции
свидетельствуют о тесной связи между
успешной сдачей экзамена по математике
студентом и его посещением занятий по
этой же дисциплине. Для изучения тесноты
связи между двумя качественными
признаками, каждый из которых состоит
из трех и более групп, вычисляют
коэффициенты взаимной сопряженности
Пирсона (
)
и Чупрова.
Для их вычисления строится вспомогательная таблица.
х у |
1 |
2 |
3 |
Итого |
1
II
III |
|
|
|
|
Итого |
|
|
|
|
Для вычисления этих
коэффициентов определяют показатель
взаимной сопряженности (
)
по формулам
=
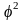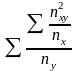– 1 или
=
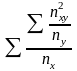– 1.
Коэффициент Пирсона рассчитывается по формуле
=
;
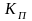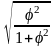Коэффициент Чупрова вычисляют по формуле
=
,
где
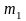– число групп первого признака;
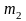– число групп
второго признака.
Чем ближе величина коэффициентов Пирсона и Чупрова к 1, тем сильнее связь между признаками.
Пример 4. Оцените связь между уровнем жизни населения и уровнем экономического развития региона с помощью показателей Пирсона и Чупрова.
Группы регионов по уровню экономического развития |
Группы регионов по уровню жизни населения |
Итого |
||
высокий |
средний |
низкий |
||
Высокий |
2 |
1 |
0 |
3 |
Средний |
2 |
1 |
2 |
5 |
Низкий |
0 |
2 |
2 |
4 |
Итого |
4 |
4 |
4 |
12 |
Решение. Рассчитаем нужные показатели
=
– 1 = (
+
)
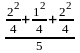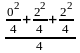– 1 = =
1,367 – 1 =
0,367.
=
=
=
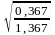0,518.
=
=
=
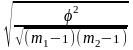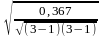0,428.
Значит, связь между уровнем экономического развития регионов и уровнем жизни населения в них средняя.