Лекция 15

Тема: Элементы квантовой механики

Вопросы:1) Волновые свойства вещества. Гипотеза де Бройля

2) Принцип неопределенности

3) Уравнение Шредингера. Частица в одномерной потенциальной яме

4) Атом водорода по квантово-механической теории.

1. В начале 20-го века стало уже ясно, что свет проявляет двойственные свойства, т.е. дуализм. Волновая природа его проявляется в интерференции и дифракции, а корпускулярная – в фотоэффекте, эффекте Комптона.

В 1924 году Луи де Бройль выдвинул гипотезу, что дуализм имеет универсальное значение и присущ также и частицам. Так, фотон обладает энергией Е = hν и импульсом . По идее де Бройля движение электрона или любой другой частицы связано с волновым процессом, т.е. частицам присуща волна с длиной .

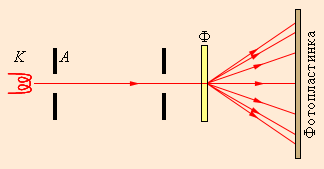В 1927 году гипотеза де Бройля подтвердилась рядом экспериментов. Так, в 1927 году Томсон направлял пучок электронов, ускоренных разностью потенциалов порядка десятков киловольт, на тонкую металлическую фольгу рис.15.1). Пройдя через фольгу, электроны давали на фотопластинке такую же дифракционную картину, как и рентгеновские фотоны.

Рис.15.1

Полученные в опытах длины волн соответствуют длине волны де Бройля. Опыты показали, что дифракционная картина наблюдается даже при небольшом числе электронов в пучке и волновые свойства присущи отдельному электрону.

Дифракционные явления наблюдались также у пучков атомов и молекул, т.е. волновые свойства присущи всем микрочастицам – молекулам, атомам, нейтронам, протонам и другим элементарным частицам. Однако, эти волны отличаются от обычных волн – их нельзя разделить на части, например, отражением и преломлением. Частица ведет себя как неделимое целое.

2. В классической механике состояние частицы определяется значением координат, импульса, энергии. Применяя законы динамики можно рассчитать траекторию движения частицы и ее местонахождение в любой момент времени.

Наличие волновых свойств, необычное поведение микрочастиц не позволяют определять их состояние методами классической механики. Нельзя говорить об определенной траектории микрочастицы и нельзя одновременно точно определить значение координаты и импульса частицы в любой момент времени. Это обстоятельство отражает одно из основных положений квантовой механики – соотношение неопределенностей Гейзенберга: произведение неопределенностей двух сопряженных переменных величин не может быть меньше постоянной Планка

ΔxΔpx ≥ h;

ΔyΔpy ≥ h;

ΔzΔpz ≥ h.

Соотношение неопределенностей означает, что, если попытаться точно определить координату микрочастицы в какой-то момент времени (Δx = 0), то погрешность (неопределенность) определения импульса частицы становится бесконечно большой. Так как импульс частицы p = mv, то соотношение неопределенностей можно записать в виде ΔxΔvx ≥ h/m. Значит, чем больше масса частицы, тем меньше неопределенность ее координаты и импульса. Поэтому принцип Гейзенберга, как и гипотеза де Бройля, применимы к микрочастицам и не проявляются в макромире.

Соотношение неопределенностей для энергии микрочастицы и времени имеет такой же вид:

ΔEΔt ≥ h.

Соотношение показывает, что для определения энергии частицы с точностью ΔE потребуется интервал времени не меньше Δt.

Соотношение неопределенностей допускает существование виртуальных частиц, которые имеют очень короткое время жизни, но не могут быть зафиксированы никакими приборами. Их параметры можно оценить с помощью законов сохранения в различных процессах взаимодействия микрочастиц. Соотношение неопределенностей объясняет, почему электрон не падает на ядро – в этом случае его координаты и импульс приобрели бы определенные значения, что не может осуществиться в микромире.

3. Дифракционная картина для электронов, прошедших через фольгу (рис.15.1) показывает, что электроны попадают на фотопластинку в местах максимума интенсивности волн де Бройля неравномерно. Наблюдается статистическое распределение частиц, которое необходимо описывать понятиями теории вероятности. Вероятностный подход положен в основу квантовой механики, он наиболее точно отражает процессы в микромире.

В 1926 году Шредингер вывел основное уравнение квантовой механики, в котором сопоставил движению микрочастицы комплексную функцию координат и времени ψ (пси-функция). Пси – функцию он назвал волновой функцией.

Для стационарных состояний частицы уравнение Шредингера имеет вид

,

где Е – полная энергия электрона, U - потенциальная энергия; - оператор

Лапласа

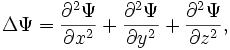
Смысл пси-функции состоит в том, что квадрат ее модуля определяет вероятность того, что частица будет обнаружена в данной точке пространства. Квантовая механика не позволяет определить местонахождение частицы в пространстве и ее траекторию. С помощью пси-функции можно только предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства. Уравнение Шредингера позволяет найти пси функцию для заданных условий и определить вероятность нахождения частицы в различных точках пространства.

Пусть частица находится в бесконечно глубокой одномерной потенциальной яме. Понятие потенциальной ямы означает, что на частицу действует сила, не позволяющая ей оторваться от источника силы и стать свободной. Например, электрон в атоме движется в поле притяжения ядра в ограниченном пространстве, т.е. находится в потенциальной яме.

Ч тобы упростить рассуждения, будем считать, что частица движется вдоль оси Х между бесконечно высокими энергетическими стенками (рис.15.2).

Рис.15.2

Расстояние между стенками l, между стенками U = 0 при 0 ≥ х ≤ l.

За стенками U = ∞ при х <0 и х > l .

Для рассматриваемого случая уравнение Шредингера имеет вид

Так как за пределы ямы частица не может попасть, то ψ(0) = ψ(l) = 0 – граничные условия. Внутри ямы U = 0, поэтому уравнение Шредингера можно записать в виде

.

Обозначим , тогда уравнение примет вид . Решение дифференциального уравнения получаем в виде ψ(х) = Аsin(kx +α).

Из условия, что ψ(0) = 0, получим Аsinα = 0. Отсюда α = 0. Из условия, что ψ(l) = 0, получим Аsinkl = 0. Это возможно при kl = ±nπ, где n = 1,2,3…

Так как , то . Отсюда получаем ряд значений энергии, которую может иметь частица в потенциальной яме

, где n = 1,2,3…

Таким образом, частица в силовом поле имеет дискретный ряд определенных значений энергии, а волновая функция также принимает ряд значений

Вид волновой функции для трех значений числа n показан на рис.15.3.

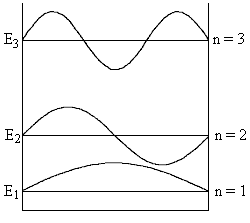
Рис.15.3