3. Введем понятие – поток n вектора напряженности через площадку s:

N=E Scosα, где α – угол между нормалью (перпендикуляром) к площадке линией напряженности. Если угол α острый, то N>0,если тупой, то N<0.

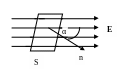
Рис.1.4

Если поле неоднородное и поверхность не плоская, то ее разбивают на бесконечно малые элементы dS так, что каждый элемент можно считать плоским, а поле однородным. Поток вектора напряженности через элемент поверхности dN=EdScosα, а через всю поверхность

Поток вектора напряженности через замкнутую поверхность равен нулю.

Пусть внутри замкнутой поверхности радиусом R, в ее центре, находится точечный заряд q. Напряженность электрического поля в точках на расстоянии R от заряда

Видно, что напряженность электрического поля одинакова во всех точках поверхности. Вычислим поток вектора напряженности через замкнутую сферическую поверхность S радиусом R, окружающую заряд.

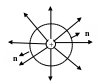
Рис.1.5

Поток вектора напряженности через замкнутую поверхность

от радиуса сферы не зависит, то есть одинаков для сферы любого радиуса, а значит и для замкнутой поверхности любой формы.

Можно показать, что поток вектора напряженности не зависит от расположения заряда и результат справедлив для любого числа зарядов внутри поверхности. Эти выводы доказывают справедливость теоремы Гаусса: поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на ε0

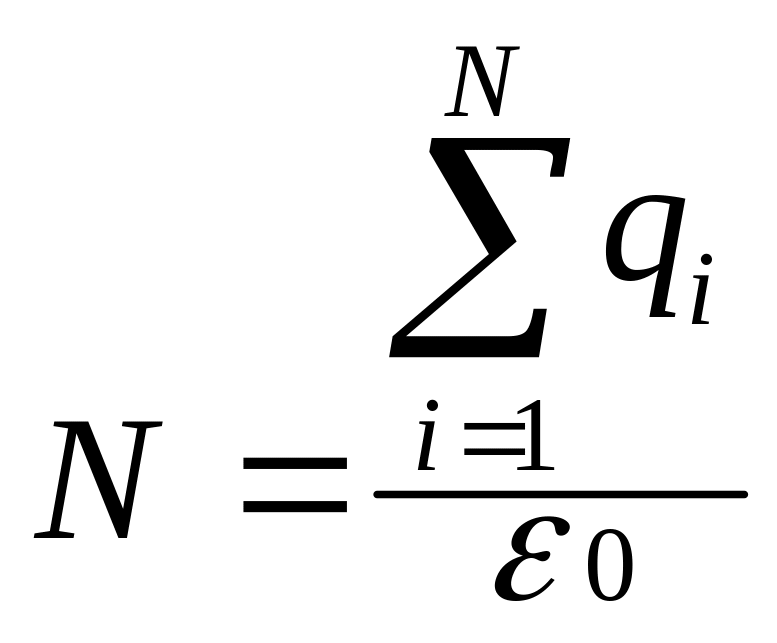
Теорема позволяет вычислить напряженность электрического поля, создаваемого заряженными телами любой формы.

Пример 1.Равномерно заряженная безграничная плоскость с поверхностной плотность заряда σ.

Поверхностная плотность заряда – это заряд, приходящийся на единицу

поверхности σ = q/S

.

Рис.1.6

Мысленно построим замкнутую поверхность в виде цилиндра с площадью основания S. Полный поток вектора напряженности сквозь цилиндрическую поверхность равен N=2ES (поток через боковую поверхность равен нулю). Полный заряд, заключенный в цилиндре q=σS. Применим теорему Остроградского – Гаусса:

.

Отсюда находим напряженность поля, создаваемого заряженной плоскостью:

.

Пример 2. Равномерно заряженный шар с зарядом q.

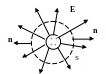
Рис.1.7

Поток вектора напряженности через замкнутую поверхность

N = E4πr² = q/ε0 .

Отсюда напряженность поля, создаваемого заряженным шаром, на расстоянии r от его центра равна

4. Пусть в однородном электрическом поле перемещается положительный заряд q из точки 1 в точку 2. На заряд действует сила в

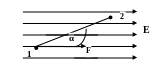
Рис.1.8

направлении вектора Е, значит, совершается работа поля A=Flcosα, она положительная, т.к. 0°<α<90°. При перемещении заряда из точки 2 в точку 1 работа такая же по величине, но отрицательна, т.к. 90°<α<180° (перемещение заряда против поля совершает внешняя сила) - работа по замкнутому контуру равна нулю. Можно показать, что работа перемещения заряда по любому замкнутому контуру в электрическом поле равна нулю.

При перемещении заряда в неоднородном электрическом поле сила F=qE, разная в разных точках, и работа поля по перемещению заряда из точки 1 в точку 2

.

1

Рис.1.9

Работа зависит от напряженности электрического поля и тоже может служить характеристикой поля. Для этого ввели понятие «разность потенциалов»

Работа электрического поля А = q(φ1 – φ2). Отсюда вытекает физический смысл разности потенциалов: разность потенциалов двух точек поля измеряется работой, совершаемой силами поля при перемещении единичного положительного заряда из одной точки в другую

φ1 – φ2 = A/q

Разность потенциалов назвали напряжением U = φ1 – φ2 и работа поля может быть представлена как А = qU. Единица измерения напряжения

[U]= Дж/Кл = В (вольт).

Таким образом. существуют две основные характеристики электрического поля: векторная – напряженность Е и скалярная – напряжение U, которые связаны соотношением E = U/d для однородного электрического поля. Отсюда единица измерения напряженности [E] = В/м.

Пусть электрическое поле создается точечным зарядом q. Можно вычислить потенциал φ в любой точке поля на расстоянии r от заряда, если вторую точку взять вдали от заряда (бесконечно удаленную), где поля практически нет:

φ1 – φ∞ = A/q, значит .

Так как φ∞ =0, то потенциал электрического поля в точке на расстоянии r от заряда равен

.

Видно, что в точках, расположенных на одинаковом расстоянии от заряда, потенциал одинаков. Линии одинакового потенциала называются эквипотенциальными, в поле точечного заряда на плоскости они имеют вид концентрических окружностей (в пространстве – сфер). В однородном электрическом поле вблизи заряженной плоскости эквипотенциальные линии параллельны друг другу и плоскости. Между эквипотенциальными линиями существует разность потенциалов, то есть напряжение.