Единицы величин
Единица величины – это конкретная величина, определенная и принятая по соглашению, с которой сравниваются другие величины того же рода.
Единицы величин появились тогда, когда у человека возникла необходимость выразить что-либо количественно. Этим «что-либо» могло быть число предметов, и тогда измерение было простым и заключалось в счете (единица величины – штука). Однако сыпучие вещества (зерно) и жидкости не поддавались штучному счету. Так возникли меры объема, ставшие единицами измерения объема. Первыми мерами длины были части тела человека (ступня, шаг, локоть). О путях формирования мер и единиц величин на Руси отмечено в первом разделе. В английской системе мер до сих пор существуют некоторые единицы, связанные с размерами тела человека. Например, фут (foot – ступня) – это средняя длина ступни человека. Размер фута равный 30,48 см был установлен в результате осреднения величины ступни людей «выходящих из храмов от заутрени в воскресенье». Размер дюйма (25,4 мм) возник как длина трех ячменных зерен, вынутых из средней части колоса и приставленных друг к другу своими концами. Так, по решению короля Эдварда II в 1324 г. появился «законный дюйм». Версий относительно возникновения такой единицы длины, как английский ярд (0,9144 м) несколько. Это может быть и расстояние от кончика носа короля Генриха I до конца среднего пальца вытянутой им вперед руки, и длина меча этого короля. Единица длины миля (1,609 м) возникла при усреднении 1000 двойных шагов человека. Таких примеров можно привести много. Локоть до сих пор является единицей национальной меры длины в Болгарии.
Разнообразие единиц измерений в мире всегда затрудняло торговые операции, поэтому все стремились к их унификации. В обозримом историческом промежутке процесс унификации единиц величин прошел по крайней мере три этапа.
На первом этапе размер единицы величины приравнивали размеру величины, воспроизводимой природной мерой, например, к локтю.
На втором этапе единицы величин закрепили в «вещественных образцах», создали эталоны длины и массы – метр и килограмм.
На третьем этапе для более точного и надежного воспроизведения ряда величин единицы величин были оторваны от «меры», от количественных характеристик свойств физических объектов, предназначенных для их воспроизведения. Например, метр остался метром, но его длина измеряется длиной пути, который проходит свет в вакууме за 1/299792458 долю секунды.
По-видимому, процесс уточнения размеров единиц продолжится, так как уже безусловно стало ясно, что изготовленные человеком вещественные (предметные) эталоны единиц величин не могут обеспечить хранение и передачу их размера с необходимой точностью.
3.1. Уравнения связи между величинами
Описание каждого свойства, характеризуемого данной величиной, производится на языке уже определенных известных величин, так как между свойствами объектов объективно существуют взаимосвязи. Если эти свойства перевести на язык величин, то они становятся моделями. Совокупность таких моделей образует систему уравнений. Различают два типа уравнений.
Первый тип – это уравнения связи между величинами – уравнения, отражающие законы природы, в которых под буквенными символами понимают физические величины. Единицы величин в этом случае не имеют значения
|
(1) |
где
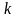– коэффициент, не зависящий от системы
единиц и лишь представляющий связь
между ними.
Например, площадь треугольника равна 0,5lh. Коэффициент =0,5 зависит только от формы фигуры, но l и h могут быть измерены в метрах, в сантиметрах, в дюймах и т.д.
Второй тип – это уравнение связи между числовыми значениями физических величин – уравнение, в котором под буквенными символами понимают числовые значения величин, соответствующие выбранным единицам.
|
(2) |
где
–
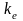числовой коэффициент, зависящий от
выбранной системы единиц.
Например, если размеры фигуры в системе СИ даны в метрах, тогда площадь треугольника равная 0,5lh (м2), т.е. =1.
Если же длина l – в метрах, а высота h – в мм, то площадь треугольника равна 0,5lh·10–6 (м2), т.е. =10–6 м2/мм.
С помощью уравнений связи между числовыми значениями величин формулируются определения одних величин на языке других и указываются способы их нахождения. Так образуется система физических величин, причем на каждом этапе развития – своя.