4.4.1 Классификация погрешностей измерений и средств измерений

Общая погрешность измерения и средства измерения не является постоянной величиной, а зависит от множества факторов. Для удобства оценки общей погрешности с привлечением закономерностей теории вероятности и методов математической статистики эти факторы классифицируют по следующим признакам (рис. 4.7).

1. По характеру проявления на: систематические, случайные, прогрессирующие (дрейфовые), грубые (промахи).

2. По способу выражения на: абсолютные, относительные, приведенные.

3. В зависимости от места возникновения на: инструментальные, методические, субъективные.

4. По влиянию внешних условий на: основные и дополнительные.

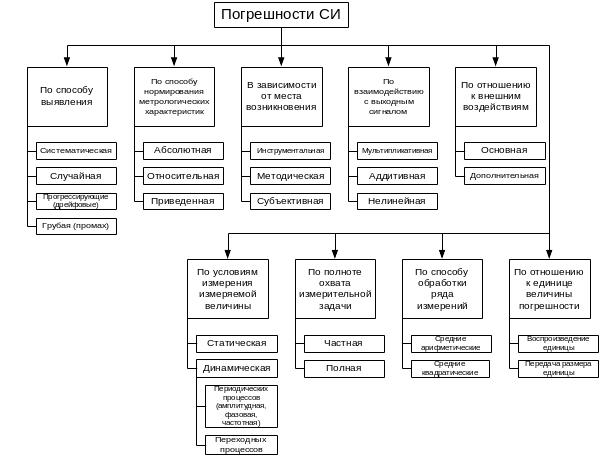
Рисунок 4.7 – Классификация погрешности измерений

Кроме того, погрешности (неопределенности) измерений классифицируют по:

• по зависимости абсолютной погрешности от значения измеряемой величины на: аддитивные, мултипликативные, нелинейные;

• в зависимости от характера измеряемой величины на: статические и динамические;

• по полноте охвата измерительной задачи на: частные и полные;

• по способу обработки ряда измерений на: средние арифметические и средние квадратические;

• по отношению к единице величины погрешности при: воспроизведении единицы или передаче размера единицы.

Выделяют также такие составляющие погрешности измерений, как погрешность метода, субъективная, погрешность отсчета и др.

Традиционный аналитический подход к оцениванию погрешностей в метрологии состоит в изучении каждой их составляющей в отдельности с последующим суммированием. Если удается количественно оценить каждую составляющую погрешности, то можно так организовать процесс измерений, чтобы хотя бы некоторая часть их не оказывала влияния на результат измерения, а другая была бы введена в виде поправок. Наибольшую долю в общей погрешности измерения составляют систематические, случайные и грубые погрешности.

Систематическая погрешность измерения (systematic error of measurement) – это составляющая погрешности измерения, которая при повторных измерениях остается постоянной или изменяется предсказуемым образом (VIM).

Опорным значением величины для систематической погрешности измерения является истинное значение величины или измеренное значение величины эталона с незначительной неопределенностью измерения, или приписанное (стандартизованное) значение величины.

Систематическая погрешность измерения равна погрешности измерения минус случайная погрешность измерения.

Необходимо иметь в виду, что при определении разности указанных погрешностей каждую из них берут со своим положительным или отрицательным знаком.

В зависимости от характера изменения систематические погрешности подразделяют на постоянные, прогрессивные и погрешности, изменяющиеся по сложному закону (периодические).

Систематическая погрешность измерения и истинные причины ее возникновения могут быть известны или неизвестны. Однако последнее время считается, что систематические погрешности современных средств измерений могут быть предсказаны, обнаружены и благодаря этому устранены путем введения поправок (поправка – значение величины, которая суммируется с неисправленным результатом измерения). При этом следует помнить, что поправка относится только к данному экземпляру средства измерения и не может быть распространена на все приборы данного типа.

Случайная погрешность измерения (random measurement error) – это составляющая погрешности измерения, которая в повторных измерениях изменяется непредсказуемым образом.(VIM).

Опорным значением величины для случайной погрешности измерения является среднее значение, получаемое в результате бесконечного числа повторных измерений одной и той же измеряемой величины.

Случайная погрешность – это составляющая погрешности измерений, изменяющаяся случайным образом при повторных измерениях одной и той же величины, которая может быть обнаружена в виде некоторого разброса результатов измерений. Она неизбежна, неустранима и всегда присутствует в результатах измерений. В то же время теория погрешностей утверждает (и это подтверждено практикой), что при большом числе измерений случайные погрешности одинакового значения, но разного знака, встречаются одинаково часто, а большие (по абсолютному значению) погрешности можно существенно уменьшить путем увеличения числа измерений. Для получения результата измерения, минимально отличающегося от действительного проводят многократные измерения с последующей математической обработкой экспериментальных данных. Обычно случайную составляющую погрешности измерений для наблюдений характеризуют дисперсией 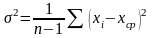или размахом .

Существенно положительную величину 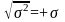называют средним квадратическим отклонением (S) или стандартным отклонением, которое получается при обработке ограниченного числа измерений. Оно является характеристикой рассеяния результатов измерений данного ряда величин вследствие случайных причин. Рассеяние результатов измерений – это явление несовпадения результатов измерений одной и той же величины в ряду измерений. Характеристикой рассеяния результатов измерений данного ряда может служить также размах.

Прогрессирующая (дрейфовая) погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени. Это понятие широко используется при изучении метрологической надежности средств измерения на транспорте и не может быть сведено к понятиям систематической и случайной составляющей погрешности измерений. Такая погрешность возникает, например, при износе измерительных наконечников в процессе измерений или при снятии отсчетов по шкале гидравлических прессов, если они начали работу на непрогретом масле и т.д.

Грубая погрешность или промах – это погрешность результата измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда. Как правило, такие погрешности возникают из-за неверной записи показаний прибора, неправильного прочтения отсчета, не совмещения конца изделия с нулем линейки и т.д.

Промахи, обнаруженные в процессе измерения обычно отбрасывают и увеличивают число измерений. Если же они выявлены при окончательной обработке результатов измерений, то их исключают с помощью специальных критериев. Например, таких, как критерии“3 ”, Романовского, Шарлье, Диксона и др.

По способу выражения погрешности делят на абсолютные, относительные, приведенные.

• АБСОЛЮТНАЯ погрешность ( 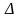) равна разнице между измеренным ( ) и действительным ( ) значением измеряемой величины

.

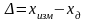• ОТНОСИТЕЛЬНАЯ погрешность ( 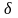) – погрешность, выраженная отношением абсолютной погрешности к результату измерений :

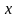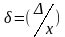или

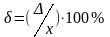
Относительная погрешность может быть выражена в долях результата измерений или в процентах от результата измерения.

Согласно РМГ 91-2009 «относительная погрешность (relative error) – это отношение 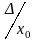погрешности измерения к опорному значению измеряемой величины », где ,

• ПРИВЕДЕННАЯ погрешность ( 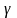) – погрешность, выраженная отношением абсолютной погрешности к некоторому нормирующему значению (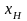 ), которое представляет собой условное принятое значение величины, постоянное во всем диапазоне измерений или в его части:

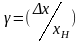или

В метрологической практике чаще всего используются относительными и приведенными погрешностями.

Пример: при измерении напряжения, действительное значение которого равно 10,0 В, средством измерения с диапазоном от 0 до 100,0 в и нормирующим значением, равным 100,0 В, результат измерения оказался 10,1 В. В этом случае абсолютная погрешность П = 10,1 – 10,0 = 0,1 В. Приведенная же П = (0,1/100) 100% =0,1%, а относительная П= (0,1/10,1) 100% =1,0%.Эти данные свидетельствуют о необходимости четкого разграничения этих понятий.

Допускается не оговаривать вид погрешности (относительная или приведенная), если после числового значения погрешности указывается, к чему относится это числовое значение, например,

– в случае относительной погрешности – «пределы допускаемой основной погрешности +0,5% от измеряемой величины»;

– в случае приведенной погрешности – «пределы допускаемой основной погрешности ±0.5% от нормирующего значения (указывается нормирующее значение)».

В соответствии с МИ 1317-2004 рекомендуется указывать численные значения характеристик погрешности измерений с использованием не более двух значащих цифр. При этом разряды последних значащих цифр при выражении результатов измерений и значений абсолютной погрешности измерений должны быть одними и теми же.

В зависимости от места возникновения погрешности различают погрешности инструментальные, методические, субъективные.

ИНСТРУМЕНТАЛЬНАЯ погрешность – погрешность применяемого средства измерения (аппаратная).

МЕТОДИЧЕСКАЯ погрешность – это погрешность, обусловленная:

• различием модели объекта измерения и модели, адекватно описывающей его свойства, которые определяют при измерении;

• влиянием способов применения СИ;

• выбором формул, по которым проводились вычисления РИ;

• влиянием факторов, не связанных со свойствами используемых СИ.

Методические погрешности не указываются нормативно-технической документации и должны определяться оператором в каждом конкретном случае.

СУБЬЕКТИВНАЯ (ЛИЧНАЯ) погрешность обусловлена погрешностью отсчета оператором показаний по шкалам СИ или по диаграммам регистрирующих приборов.

Они могут быть вызваны:

• состоянием оператора,

• несовершенством органов чувств,

• эргономическими свойствами СИ.

Характеристики личной погрешности оператора определяются на основе нормированной номинальной цены деления шкалы прибора с учетом способности «среднего оператора» к интерполяции в пределах деления шкалы.

Методические и субъективные составляющие погрешностей измерения оказывают большое влияние на результат измерения. Они целиком зависят от квалификации оператора: выбора им необходимого средства измерения и способов его применения; от эргономических свойств средства измерения; от выбранной модели для описания объекта измерения и многих других факторов. Эти составляющие погрешности измерения не могут быть указаны в нормативной документации и должны быть определены в каждом конкретном случае. Поэтому к квалификации операторов предъявляются высокие требования.

По влиянию внешних факторов на погрешность измерения различают погрешности основные и дополнительные.

Основная погрешность – это погрешность, определяемая в нормальных условиях применения СИ. Для каждого типа СИ такие условия (влажность, температура, давление и т д.)нормированы.

Дополнительная погрешность – погрешность, возникающая из-за отклонения какого либо из влияющих факторов, от нормированных значений.

В зависимости от характера изменения измеряемой величины погрешности могут быть статическими или динамическими:

• статическая погрешность – погрешность средства измерения, применяемого для измерения величины, принимаемой за неизменную;

• динамическая погрешность – погрешность средства измерения, возникающая дополнительно при измерении переменной величины и обусловленная несоответствием реакции СИ на скорость (частоту) измеряемого сигнала.

По полноте охвата измерительной задачи погрешности разделяют на:

• частная погрешность – составляющая погрешности результата косвенных измерений, обусловленная погрешностью измерения одной из величин;

• полная погрешность – погрешность результатов косвенных измерений, обусловленная воздействием всех частных погрешностей.

При обработке ряда измерений погрешности оценивают следующими значениями:

• средним арифметическим – ;

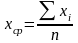• среднимквадратическим отклонением (СКО) – ;

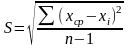• оценкой СКО измерений – .

Погрешности измерений могут возникнуть при воспроизведении единицы величины или при передаче ее размера.

Погрешности при воспроизведении единицы величины – это погрешность результатов измерения, выполняемых при воспроизведении единицы величины (обычно с помощью государственных эталонов);

Погрешности при передаче размера единицы – это погрешность результата измерения, возникающая при передаче размера единицы величины последующим средствам измерений.

В практике метрологических измерений встречаются все виды и сочетания погрешностей. Установить заранее, какие из них будут превалировать трудно. В любом случае погрешность должна быть оценена. При этом точность оценивания может быть разной и определяться объемом исходной информации и задачей измерения. В настоящее время различают измерения с «точным», приближенным и предварительным оцениванием.

При измерениях с «точным» оцениванием погрешности учитывают индивидуальные метрологические свойства, каждого из применяемых средств измерений, анализируют метод и контролируют и учитывают условия измерения.

При измерениях с приближенным оцениванием погрешности учитывают только нормативные метрологические характеристики средств измерений и оценивают влияние на результат лишь отклонений условий измерений от нормальных. Измерения с предварительным оцениванием погрешностей проводят по типовым методикам, в которых указываются методы и условия измерений, типы и погрешности рекомендуемых средств измерений, а также возможная погрешность результата.

При технических измерениях чаще всего пользуются двумя последними способами оценивания погрешностей результатов измерений.

Распространенной ошибкой при оценивании результатов и погрешностей измерений при использовании для расчетов средств вычислительной техники является вычисление и их запись с чрезмерно большим числом значащих цифр.

Для технических измерений считается допустимой погрешность оценивания погрешности в 15-20%. В связи с этим считается, что в численных показателях погрешностей должно быть не более двух значащих цифр, а наименьшие разряды числовых значений результатов измерений и численных показателей точности должны быть одинаковыми.

Практикой выработаны следующие правила округления результатов и погрешностей измерений выработаны:

1. Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются. Если десятичная дробь в числовом значении результата измерения оканчивается нулями, то нули отбрасываются только до того разряда, который соответствует разряду погрешности. Например: результат 4,0700, погрешность – 0,001, результат округляют до 4,070.

2. Если цифра старшего из отбрасываемых разрядов меньше 5, то остающиеся цифры числа не изменяют. Например, при сохранении четырех значащих цифр, число 253435 округляют до 253400, а число 253,435 – до 253,4.

3. Если цифра старшего из отбрасываемых разрядов больше или равна 5, но за ней следуют цифры, отличные от нуля, то последнюю оставляемую цифру увеличивают на единицу. Например, при сохранении трех значащих цифр число 18598 округляют до 18600, а число 182,56 – до 183.

4. Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или равны нулю, то последнюю сохраняемую не изменяют, если она четная и увеличивают, если нечетная. Например, число 22,5 при сохранении двух значащих цифр округляют до 22, а число 23,5 – до 24.