10. Экстремум функции. Необходимые и достаточные условия его существования.
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Пусть
дана функция
и
—
внутренняя точка области определения
f.
Тогда
x0 называется точкой локального максимума функции f, если существует проколотая окрестность
такая,
что
x0 называется точкой локального минимума функции f, если существует проколотая окрестность такая, что
Если неравенства выше строгие, то x0 называется точкой строгого локального максимума или минимума соответственно.
x0 называется точкой абсолютного (глобального) максимума, если
x0 называется точкой абсолютного минимума, если
Значение функции f(x0) называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.
Необходимые условия существования локальных экстремумов
Лемма Ферма. Пусть функция
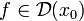дифференцируема
в точке локального экстремума x0.
Тогда:
.
Если в точке экстремума существует первая частная производная (по какому-либо аргументу), то она равна нулю.
Достаточные условия существования локальных экстремумов
Пусть функция
непрерывна
в
и
существуют конечные или бесконечные
односторонние производные
.
Тогда при условии
x0 является точкой строгого локального максимума. А если
то x0 является точкой строгого локального минимума.
Заметим, что при этом функция не дифференцируема в точке x0
Пусть функция f непрерывна и дважды дифференцируема в точке x0. Тогда при условии
и
x0 является точкой локального максимума. А если
и
то x0 является точкой локального минимума.
11. Точки перегиба функций, выпуклость и вогнутость функции.
Точка перегиба функции внутренняя точка x0 области определения f, такая что f непрерывна в этой точке, существует конечная или определенного знака бесконечная производная в этой точке, и x0 является одновременно концом интервала строгой выпуклости вверх и началом интервала строгой выпуклости вниз, или наоборот.
Неофициальное: В этом случае точка (x0;f(x0)) является точкой перегиба графика функции, то есть график функции f в точке (x0;f(x0)) «перегибается» через касательную к нему в этой точке: при x < x0 касательная лежит под графиком f, а при x > x0 — над графиком f (или наоборот)
Необходимое условие
существования точки перегиба:
если функция f(x), дважды дифференцируемая
в некоторой окрестности точки x0,
имеет в x0
точку перегиба, то
.
Достаточное условие
существования точки перегиба:
если функция f(x)
в некоторой окрестности точки x
k
раз непрерывно дифференцируема, причем
k
нечётно и
,
и
при
,
а
,
то функция f(x)
имеет в x0
точку перегиба.
Выпуклость и вогнутость
свойство графика функции у = f (x) (кривой), заключающееся в том, что каждая дуга кривой лежит не выше (не ниже) своей хорды; в первом случае график функции f (x) обращён выпуклостью книзу (вогнутостью кверху) и сама функция называется выпуклой (рис. 1, а), во втором — график обращён вогнутостью книзу (выпуклостью кверху) и функция называется вогнутой (рис. 1, б). Если существуют производные f '(x) и f "(х), то первый случай имеет место при условии, что f "(x) ≥ 0, а второй при f "(x) ≤ 0 (во всех точках рассматриваемого промежутка). Выпуклость (книзу) можно охарактеризовать также тем, что дуга кривой лежит не ниже касательной, в окрестности любой своей точки (рис. 2, a), а вогнутость (книзу) — тем, что дуга кривой лежит не выше касательной (рис. 2, б). Аналогично определяются В. и в. поверхности.
Рис. 1 к ст. Выпуклость и вогнутость.
Рис. 2 к ст. Выпуклость и вогнутость.