13. Функции многих переменных и их непрерывность.

Переменная (с областью изменения ) называется функцией независимых переменных в множестве , если каждой паре их значений из по некоторому правилу или закону ставится в соответствие одно определенное значение из множества . Множество v область определения функции, множество v область ее значений. Функциональная зависимость от обозначается так: и т.п. Выберем в пространстве систему координат , изобразим на плоскости множество ; в каждой точке этого множества восстановим перпендикуляр к плоскости и отложим на нем значение . Геометрическое место полученных таким образом точек и является пространственным графиком функции двух переменных.

Число А называют пределом функции f (x) при ( ), если

,

или

.

Оба эти определения эквивалентны.

Кроме этого понятия предела, которое обобщает понятие предела для функции одного переменного, для функций многих переменных существует и еще одно специфическое понятие, которого не было для функций одного переменного – так называемые повторные пределы. Опишем его на примере функции двух переменных .

Пусть задана функция двух переменных x и y. Пусть точка стремится к точке с координатами . Тогда то понятие предела, которое дано выше, называется двойным пределом и обозначается так: .

Будем теперь подходить к точке двумя путями (см. рис. 8.1). Первый выглядит так: сначала из точки перейдем в точку , двигаясь параллельно оси OY, а затем из этой точки перейдем в точку , двигаясь параллельно оси OX. В применении к функции это означает, что мы сначала перешли к пределу , получив некоторую функцию , а затем уже нашли , получив так называемый повторный предел

14. Производные и дифференциалы функций многих переменных.

Частные производные первого порядка и их геометрическое истолкование

Пусть задана функция z = ƒ (х; у). Так как х и у — независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной х приращение Δх, сохраняя значение у неизменным. Тогда z получит приращение, которое называется частным приращением z по х и обозначается ∆_хz. Итак,

Δ_хz=ƒ(х+Δх;у)-ƒ(х;у).

Аналогично получаем частное приращение z по у:

Δ_уz=ƒ(x;у+Δу)-ƒ(х;у).

Полное приращение Δz функции z определяется равенством

Δz = ƒ(х + Δх;у + Δу)- ƒ(х; у).

Если существует предел

то он называется частной производной функции z = ƒ (х; у) в точке М(х;у) по переменной х и обозначается одним из символов:

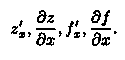
Частные производные по х в точке М₀(х₀;у₀) обычно обозначают символами

Аналогичноопределяется и обозначается частная производная от z=ƒ(х;у) по переменной у:

Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции ƒ(х;у) находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х или у считается постоянной величиной).

Пример 44.1. Найти частные производные функции z = 2у + е^{х2-у +1}. Решение:

Г еометрический смысл частных производных функции двух переменных

Графиком функции z= ƒ (х; у) является некоторая поверхность (см. п. 12.1). График функции z = ƒ (х; у₀) есть линия пересечения этой поверхности с плоскостью у = у_о. Исходя из геометрического смысла производной для функции одной переменной (см. п. 20.2), заключаем, что ƒ'x(х_о;у_о) = tg а, где а — угол между осью Ох и касательной, проведенной к кривой z = ƒ (х; у₀) в точке Мо(хо;уо; ƒ(хо;уо)) (см. рис. 208).

Аналогично, f'y (х₀;у₀)=tgβ.

44.2. Частные производные высших порядков

Частные производные называют частными производными первого порядка. Их можно рассматривать как функции от (х;у) є D. Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:

Аналогично определяются частные производные 3-го, 4-го и т. д. порядков.

Так, и т.д.

Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной.Таковыми являются, например,