
- •1.Понятие множества. Операции производимые над множествами.
- •2. Числа. Числовые множества. Числовая ось. Окрестности точки.
- •3. Отображения между множествами. Функции и их опредиления.
- •4. Элементарные функции. Их свойства и графики.
- •5. Числовые последовательности. Предел числовой последовательности.
- •6. Непрерывность функции в точке. Предел функции в точке.
- •7. Производная функции. Геометрический и физический её смысл.
- •Определение производной функции через предел
- •1) Физический смысл производной.
- •2) Геометрический смысл производной.
- •8. Производные от элементарных функций. Таблица производных.
- •9. Дифференциал функций и его применение для приближённых вычислений..
- •10. Экстремум функции. Необходимые и достаточные условия его существования.
- •11. Точки перегиба функций, выпуклость и вогнутость функции.
- •12. Типовое исследование непрерывных и дифференцируемых функций.
- •13. Функции многих переменных и их непрерывность.
- •14. Производные и дифференциалы функций многих переменных.
- •15. Первообразная и непосредственный интеграл от функции.
- •Непосредственное интегрирование
- •16. Методы вычисления непосредственных интегралов.
- •18. Производные высших порядков. Методы их вычисления.
- •17. Определённый интеграл и способы его вычисления.
- •Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной
- •19. Ряды Маклорана и Тейлора дифференцируемых функций.
- •20. Общее понятие о линейных векторных пространствах. Их определение.
- •21. Базисы в лвп. Их преобразования. Координатное представление векторов.
- •22. Основные операции производимые над векторами.
- •23. Линейные отображение в лвп. Предоставление линейных преобразований матрицами..
- •24. Определение матриц. Основные операции, осуществляемые над матрицами.
- •25. Системы векторов. Ранг системы векторов. Ранг матрицы.
- •Ранг матрицы
- •26. Определители матриц. Правила и методы их вычисления.
- •27. Системы линейных уравнений и методы их решений.
20. Общее понятие о линейных векторных пространствах. Их определение.
Линейное,
или векторное
пространство
![]() над
полем
P
— это непустое
множество
L,
на котором введены операции
над
полем
P
— это непустое
множество
L,
на котором введены операции
сложения, то есть каждой паре элементов множества
 ставится
в соответствие элемент того же множества,
обозначаемый
ставится
в соответствие элемент того же множества,
обозначаемый
 и
иумножения на скаляр (то есть элемент поля P), то есть любому элементу
 и
любому элементу
и
любому элементу
 ставится
в соответствие единственный элемент
из
,
обозначаемый
ставится
в соответствие единственный элемент
из
,
обозначаемый
 .
.
При этом на операции накладываются следующие условия:
 ,
для любых
(коммутативность
сложения);
,
для любых
(коммутативность
сложения); ,
для любых
,
для любых
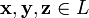 (ассоциативность
сложения);
(ассоциативность
сложения);существует такой элемент
 ,
что
,
что
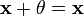 для
любого
(существование
нейтрального элемента относительно
сложения),
в частности L
не пусто;
для
любого
(существование
нейтрального элемента относительно
сложения),
в частности L
не пусто;для любого существует такой элемент
 ,
что
,
что
 (существование
противоположного элемента относительно
сложения).
(существование
противоположного элемента относительно
сложения). (ассоциативность
умножения на скаляр);
(ассоциативность
умножения на скаляр);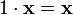 (унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор).
(унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор). (дистрибутивность
умножения на вектор относительно
сложения скаляров);
(дистрибутивность
умножения на вектор относительно
сложения скаляров); (дистрибутивность
умножения на скаляр относительно
сложения векторов).
(дистрибутивность
умножения на скаляр относительно
сложения векторов).
Элементы множества L называют векторами, а элементы поля P — скалярами. Свойства 1-4 совпадают с аксиомами абелевой группы.
Векторное пространство является абелевой группой по сложению.
Нейтральный элемент является единственным, что вытекает из групповых свойств.
 для
любого
.
для
любого
.Для любого противоположный элемент является единственным, что вытекает из групповых свойств.
 для
любого
.
для
любого
. для
любых
для
любых
 и
.
и
. для
любого
.
для
любого
.
21. Базисы в лвп. Их преобразования. Координатное представление векторов.
Любой декартовой системе координат на плоскости или в трехмерном пространстве (также и в пространстве другой размерности) может быть сопоставлен базис, состоящий из векторов, каждый из которых направлен вдоль своей координатной оси. Это относится и к прямоугольным декартовым координатам (тогда соответствующий базис называется ортогональным), так и к косоугольным декартовым координатам (которым будет соответствовать неортогональный базис).
Часто удобно выбрать длину (норму) каждого из базисных векторов единичной, такой базис называется нормированным.
Наиболее часто базис выбирают ортогональным и нормированным одновременно, тогда он называется ортонормированным.
В любом векторном пространстве базис можно выбрать различным образом (поменяв направления его векторов или их длины, например).

Декартовы координаты в трехмерном пространстве (левая (на рисунке слева) и правая (справа) декартовы системы координат (левый и правый базисы). Принято по умолчанию использовать правые базисы (это общепринятое соглашение, если только какие-то особые причины не заставляют от него отойти — и тогда это оговаривается явно). Базисом, соответствующим такой системе координат является тройка векторов, каждый из которых направлен вдоль какой-то из осей (изображаются три базисных вектора как правило исходящими из общего начала).
Обозначение векторов базиса может быть в принципе произвольным. Часто используют какую-нибудь букву с индексом (числовым или совпадающим с названием координатной оси), например:
![]() или
или
![]()
— типичные обозначения базиса двумерного пространства (плоскости).
![]() или
или
![]()
—
трехмерного
пространства. Для трехмерного пространства
часто по традиции используется и
обозначение
![]()
Представление
какого-то конкретного (любого) вектора
![]() пространства
в виде линейной комбинации векторов
базиса (суммы базисных векторов числовыми
коэффициентами), например
пространства
в виде линейной комбинации векторов
базиса (суммы базисных векторов числовыми
коэффициентами), например
![]()
или
![]()
или,
употребляя знак суммы Σ:

называется разложением этого вектора по этому базису.
Числовые
коэффициенты (ax,ay,az)
называются коэффициентами разложения,
а их набор в целом — представлением
(или представителем) вектора
в
базисе
![]() (Разложение
вектора по конкретному базису единственно;
разложение одного и того же вектора по
разным базисам — разное, то есть
получается разный набор конкретных
чисел, однако в результате при суммировании
— как показано выше — дают один и тот
же вектор).
(Разложение
вектора по конкретному базису единственно;
разложение одного и того же вектора по
разным базисам — разное, то есть
получается разный набор конкретных
чисел, однако в результате при суммировании
— как показано выше — дают один и тот
же вектор).
Базис Га́меля (англ. Hamel basis) — множество векторов в линейном пространстве, таких, что любой вектор пространства может быть представлен в виде некоторой их конечной линейной комбинации (полнота базиса), и такое представление для любого вектора единственно.
Критерием единственности решения задачи разложения вектора по полной системе векторов является линейная независимость векторов, входящих в полную систему. Линейная независимость означает, что всякая линейная комбинация векторов системы, в которой хотя бы один коэффициент ненулевой, имеет ненулевую сумму. То есть это эквивалентно единственности разложения нулевого вектора.
В случае линейных пространств, когда всякий ненулевой коэффициент обратим, линейная независимость эквивалентна невозможности выразить какой-либо вектор полной системы линейной комбинацией остальных векторов. (В более общей ситуации — модулей над кольцами — эти два свойства неэквивалентны). Невозможность выразить никакой вектор базиса через остальные означает минимальность базиса как полной системы векторов — при удалении любого из них теряется полнота.
В вопросе о существовании базисов основной является следующая лемма (доказательство этой леммы в общем случае неконструктивно и использует аксиому выбора):
Лемма. Пусть S1 — полная, а S2 — линейно независимая система векторов. Тогда система S1 содержит набор векторов, дополняющий S2 до базиса пространства V.
Следствием этой леммы являются утверждения:
Каждое линейное пространство обладает базисом.
Базис пространства можно выделить из любой полной системы векторов.
Всякую линейно независимую систему можно дополнить до базиса пространства V.
Любые два базиса в линейном пространстве равномощны, так что мощность базиса — величина, независящая от выбора базисных векторов. Она называется размерностью пространства (обозначается dim V). Если линейное пространство имеет конечный базис, его размерность конечна и оно называется конечномерным, в противном случае его размерность бесконечна, и пространство называется бесконечномерным.
Выбранный базис линейного пространства позволяет ввести координатное представление векторов, чем подготавливается использование аналитических методов.
Линейное отображение из одного линейного пространства в другое однозначно определено, если задано на векторах какого-нибудь базиса. Комбинация этого факта с возможностью координатного представления векторов предопределяет применение матриц для изучения линейных отображений векторных пространств (в первую очередь — конечномерных). При этом многие факты из теории матриц получают наглядное представление и приобретают весьма содержательный смысл, когда они выражены на языке линейных пространств. И выбор базиса при этом служит хоть и вспомогательным, но в то же время ключевым средством.
Векторы
 пространства
пространства
 образуют
базис тогда и только тогда, когда
определитель
матрицы, составленной из координатных
столбцов этих векторов, не равен 0:
образуют
базис тогда и только тогда, когда
определитель
матрицы, составленной из координатных
столбцов этих векторов, не равен 0:
 .
.В пространстве всех многочленов над полем один из базисов составляют степенные функции:
 .
.Понятие базиса используется в бесконечномерном случае, например вещественные числа образуют линейное пространство над рациональными числами и оно имеет континуальный базис Гамеля и, соответственно, континуальную размерность.
Преобразования базисов и координат, криволинейные координаты
Преобразования базисов и координат
Взаимные, сопряженные базисы
В дальнейшем речь пойдет о базисах в трехмерном пространстве.
Определение. Базисы ri , rk называются взаимными или сопряженными, если выполнено условие (ri , rk) =
 .
.Теорема. Для любого базиса ri существует единственный взаимный базис.
Из условия r1
 r2
, r1
r3
, поэтому этот вектор надо искать в виде
c[r2 , r3], из условия (r1 , r1) = 1 находится
множитель c. Таким образом,
r2
, r1
r3
, поэтому этот вектор надо искать в виде
c[r2 , r3], из условия (r1 , r1) = 1 находится
множитель c. Таким образом,
r1 = [r2 , r3]/( r1 , r2 , r3 ), r2 = [r3 , r1]/( r1 , r2 , r3 ), r3 = [r1 , r2]/( r1 , r2 , r3 ).
Любой вектор пространства можно разложить по базисам
x =
 xk
rk =
rk
xk .
xk
rk =
rk
xk .Координаты xk называются ковариантными координатами, а xk – контравариантными координатами.
Соглашение 1. В любом выражении, состоящем из некоторого числа сомножителей наличие индекса у двух сомножителей на разных уровнях будет означать суммирование по этому индексу от 1 до 3. Следует придерживать единого порядка написания индексов суммирования. Договоримся при написании этих индексов следовать правилу: «левый внизу, правый вверху».
Соглашение 2. Иногда, если не возникает путаницы, стрелка над вектором будет опускаться. Тоже самое касается жирности шрифта для обозначения вектора.
Например, формулы разложений по базисам будут выглядеть следующим образом
x = xk rk = rk xk .
Еще один пример: ai
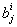 cj
=
cj
=
 ai
cj
.
ai
cj
.Найдем выражение для ко и контравариантных координат
x = xi ri = ri xi
xi = (x, ri ), xi = (x, ri) (1).
Подставляя выражения для координат в разложения вектора, получим формулы Гиббса
x = (x, ri ) ri = ri (x, ri) (2)
Подставим выражения x из формул Гиббса (2) в (1)
xi = (x,rj )(rj,ri) = xj gji (3)
xi = (rj,ri) (x,rj ) = gji xj (4)
Матрицы gji = (rj,ri), gji = (rj,ri) симметричны и называются метрическими тензорами. Беря в качестве x в формуле (2) вектора rj , rj получим формулы, связывающие векторы взаимных базисов с помощью метрических тензоров
rj = gji ri
rj = ri gji .
Подобные операции носят название операций поднимания и опускания индекса с помощью метрического тензора. Умножим первое равенство на rk второе на rk получим
 =
gji gik
=
gji gik =
gik gji .
=
gik gji .Эти равенства показывают, что матрицы метрических тензоров взаимно обратные.
