18. Точечные и интервальные оценки параметров распределения случайных величин

точечная оценка характеристики генеральной совокупности – это число, определяемое по выборке. Основой всех оценок является выборка. Существует 3 способа получения точечных оценок: метод максимального правдоподобия, метод моментов, метод наименьших квадратов.

Поскольку все оценки являются случайными по своей природе, т.к они рассчитываются по выборке, то значения этих оценок недостаточно для полной информации об оценках. Чтобы оценить влияние выборочных оценок, нужно оказать среднюю, предельную ошибку. Для этого вводят интервальные оценки. Интервальные оценки представляют собой интервалы со случайными границами, причем эти интервалы строятся так, что с наперед заданной информацией, оценка и оцениваемый параметр «накрывается» этим интервалом.

19. Метод максимального правдоподобия (Фишере) точечного оценивания параметров распределения случайных величин. Примеры.

Метод максимального правдоподобия основывается на предположении, что в выборке реализуется наиболее вероятные значения случайной величины (из генер. совокупности). В соответствие с этим фун-я распределения или фун-я плотности вероятности имеет макс.значение. Предположим, что выборочные значения статистически независимы и => фун-я плотности вероятности представлена в виде произведения этих фун-й вероятности для выборочных значений. Матем:ƒ(х₁, х₂, ….х_n, Θ₁….Θ_m). Где х – выбор.значения, а Θ – параметры. Так как х₁ стат. независима, то ƒ(х₁, х₂, ….х_n, Θ₁….Θ_m) = ƒ(х₁, Θ₁….Θ_m) ƒ(х₂, Θ₁….Θ_m)….. ƒ(х_n, Θ₁….Θ_m). В соответствии с идей метода макс. Правдоподобия на данных выборочных значениях, фун-я выборочных значений принимает макс.значение. Θ₁ Θ2 Θ3 фун-я вероятности обращается в ноль и бедет наилучшей оценкой для неизвестных параметров распределения.

Пример. Пусть время t до выхода из строя группы компьютеров на испытательном стенде описывается показательным распределением: единственный параметр которого λ неизвестен. Найти методом максимального правдоподобия оценку параметра λ

Р е ш е н и е. Испытав n компьютеров, мы получим выборку объёмом n : t₁, ….t_n. Функция плотности вероятности совместного распределения значений t₁, ….t_n имеет вид:

ƒ(t₁, t₂, ….t_n, λ) = λe^-λt₁ λe^-λt₂…. λe^-λt_n = λⁿ e^-λt₁ e^-λt₂…. e^-λt_n поскольку выражение для функции плотности вероятности представляет собой произведение экспонент, то лучше воспользоваться логарифмической формой функции правдоподобия:

ln ƒ(t₁, t₂, ….t_n, λ) = ln [λⁿ e^-λt₁ e^-λt₂…. e^-λt_n ] = n lnλ – λ (t₁ + t₂ + ….+ t_n). Уравнение максимального правдоподобия будет иметь вид:

– (t₁ + t₂ + ….+ t_n) = 0 Как было установлено в теории вероятностей, математическое ожидание для показательного распределения равно М(Х) = и обозначая , получим:

20. Метод моментов (Пирсона) точечного оценивания параметров распределения случайных величин. Примеры.

Идея метода моментов заключается в приравнивании теоретических и соответствующих им эмпирических моментов, причём число моментов и, следовательно, число уравнений для определения неизвестных параметров распределений берется равным числу параметров. Напомним, что для случайной величины определены её числовые характеристики – начальные и центральные моменты. теоретическим моментом к-го порядка называется соотношение вида: М_к^т = .Эмпирическим моментом к-го порядка для несгруппированных данных называется соотношение вида: М_к^э=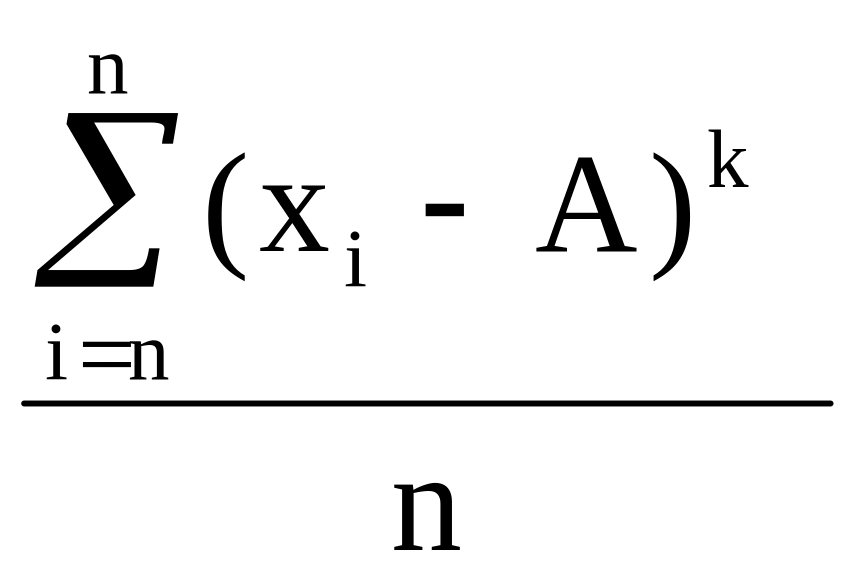 . Если принять А = 0, то моменты в этом случае называются начальными. Обычно их обозначают малыми латинскими буквами. , 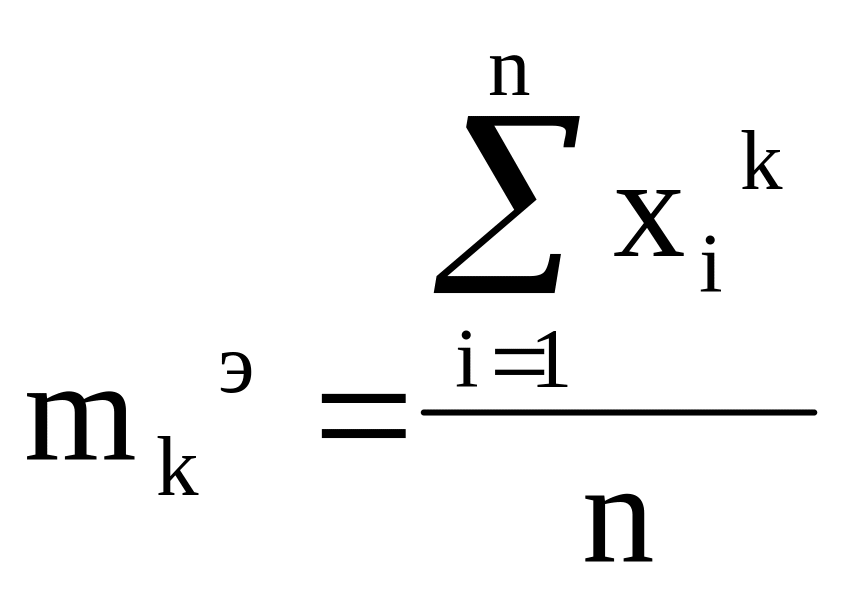. Например, начальный момент первого порядка m₁ - есть математическое ожидание. Если принять А = m₁, то моменты называются центральными. Обычно их обозначают малыми греческими буквами. μ_к ^T = , μ_к ^Э =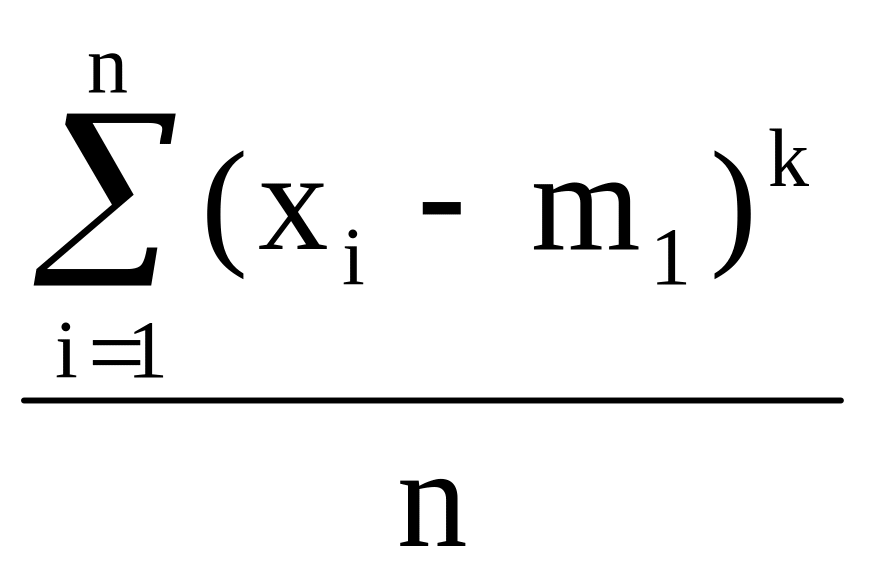 .Например, μ₂ - есть дисперсия. В случае непрерывных случайных величин в теоретических моментах суммы заменяются интегралами с бесконечными пределами.

21. Интервальное оценивание для математического ожидания, если известна заранее дисперсия распределения.

22. Интервальное оценивание для дисперсии, если известно заранее математическое ожидание распределения.

23. Интервальное оценивание для математического ожидания и дисперсии, если не известны заранее значения математическое ожидания и дисперсия распределения.

24. Статистическое оценивание с помощью проверки статистических гипотез. Ошибки первого и второго рода.

Стандартными задачами математической статистики являются задачи определения класса (вида) распределения генеральной совокупности и определение её основных числовых характеристик. Эти задачи математическая статистика решает в виде выдвижения гипотез, а не прямым расчетом. Это связано с тем, исходные данные для статистических расчетов являются случайными величинами и полученные результаты расчета тоже есть случайные величины. Поэтому каждый расчетный результат должен быть дополнен вероятностью его правильности (или ошибки), следовательно, он является гипотетическим.

Определение 1. Статистической гипотезой называют гипотезу о виде неизвестного распределения или о параметрах известного распределения.

Наряду с данной гипотезой рассматривают и противоречащую ей гипотезу. В случае, когда выдвинутая гипотеза отвергается, обычно принимается противоречащая ей гипотеза.

Определение 2. Нулевой (основной) называют выдвинутую гипотезу H₀. Конкурирующей (альтернативной) называют гипотезу H₁, которая противоречит основной.

Проверку правильности или неправильности выдвинутой гипотезы проводят статистическими методами. В результате такой проверки может быть принято правильное или неправильное решение. Поэтому различают ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.