5. Признак Даламбера сходимости рядов с неотрицательными членами.

Теорема 7. Пусть дан ряд с положительными членами и существует предел . Тогда a) при ряд сходится; б) при ряд расходится. Доказательство. а) Пусть и . Докажем, что ряд сходится. По определению предела числовой последовательности для любого существует номер такой, что при выполняется неравенство . Отсюда следует, что (8) Так как , то можно взять настолько малым, что будет вы­полнено неравенство . Полагая , на основа­нии правого из неравенств (8) имеем , или для Придавая эти значения, из послед­него неравенства получаем 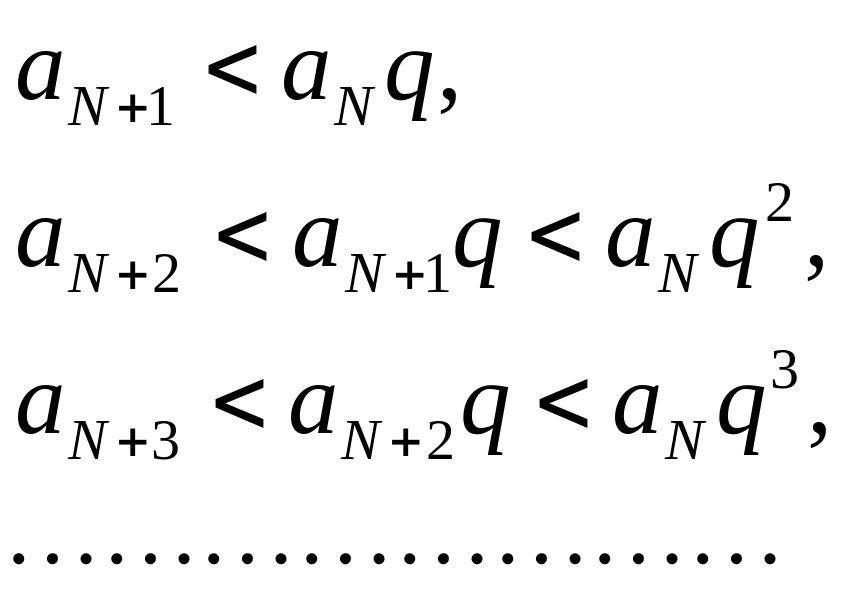т. е. члены ряда (9) меньше соответствующих членов ряда, составленного из элемен­тов геометрической прогрессии: (10) Так как , то ряд (10) сходится. Тогда согласно признаку сравнения ряд (9) также сходится. Но ряд (9) получен из данного ряда в результате отбрасывания конечного числа первых членов, следовательно, по теореме 1 ряд сходится. б) Пусть теперь . Докажем, что ряд расходится. Возьмем настолько малым, чтобы . Тогда при в силу левого из неравенств (8) выполняется неравенство или . Таким образом, члены ряда, начиная с неко­торого номера , возрастают с увеличением их номеров, т. е. об­щий член ряда не стремится к нулю при . Следовательно, согласно теореме 4 ряд расходится. Теорема доказана.

6. Интегральный признак Коши – Маклорена сходимости рядов с неотрицательными членами. Примеры.

Теорема8. Пусть дан ряд ,члены которого являются значениями некоторой функции , положительной, непрерывной и убывающей на полуинтервале . Тогда, если сходится, то сходится и ряд ; если же расходится, то ряд расходится. Доказательство. Рассмотрим криволинейную трапецию, ограниченную сверху графиком функции , с боковых сто­рон прямыми , снизу осью Ох Впишем в эту трапе­цию и опишем около нее две ступенчатые фигуры, состоящие из прямоугольников с основаниями и высотами . Тогда, принимая во внимание геометрический смысл определенного инте­грала, имеем , или, короче, . Отсюда получаем , (11) и ,(12) где — частичные суммы рассматриваемого ряда. Пусть интеграл сходится. Следовательно, существует .Так как , то последовательность возрастает с увеличением и ограничена сверху своим пределом: . Из неравенства (11) следует, что , т. е. последовательность частичных сумм ряда ограничена. По теореме 14.5 ряд сходится. Пусть теперь интеграл расходится. В этом случае при (как монотонно возрастающая неограниченная последовательность). Из неравенства (12) следует, что при , т. е. последо­вательность частичных сумм ряда расходится и, следо­вательно, ряд расходится. Теорема доказана.