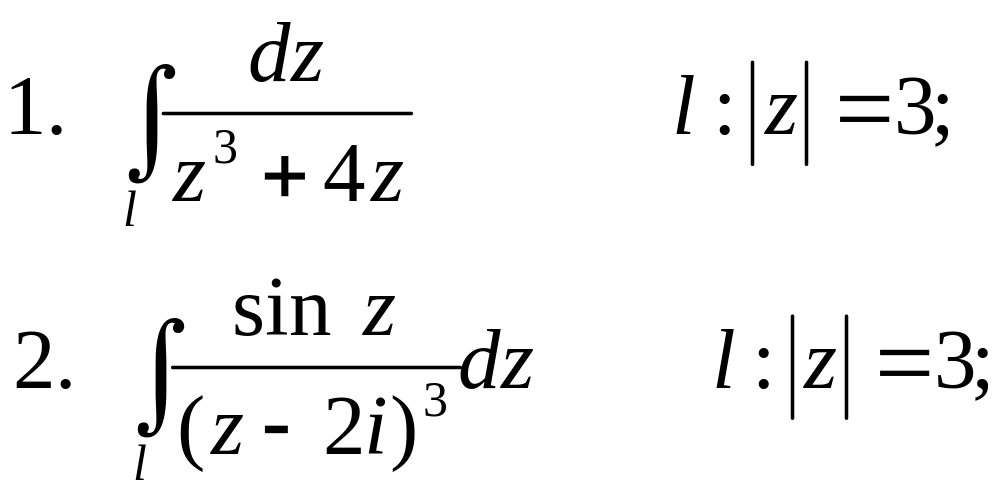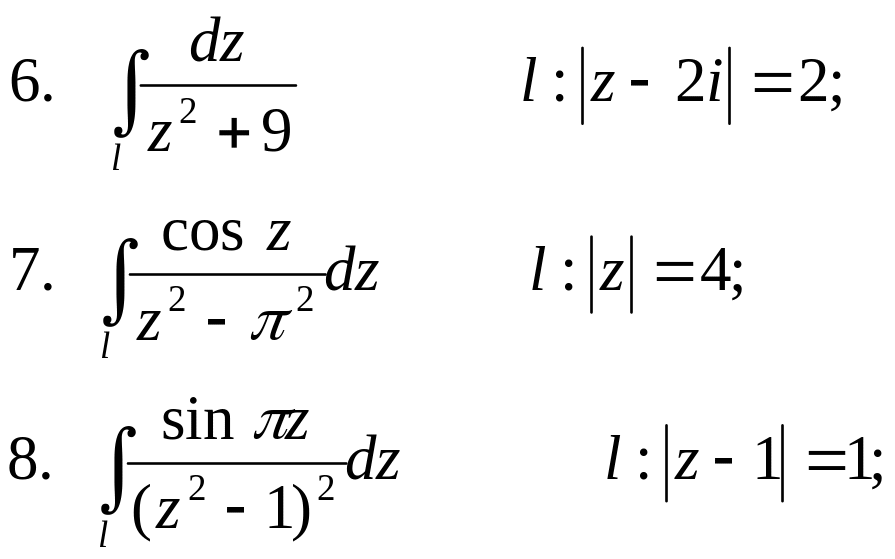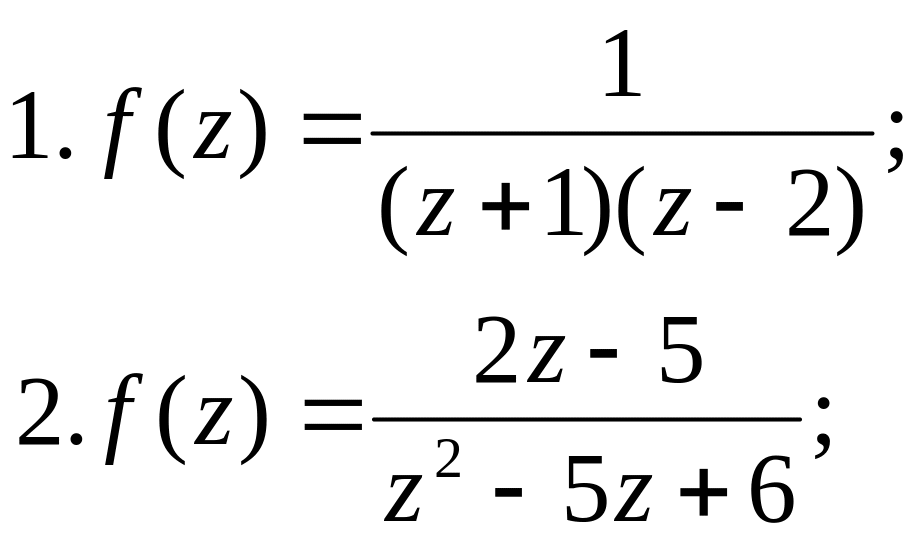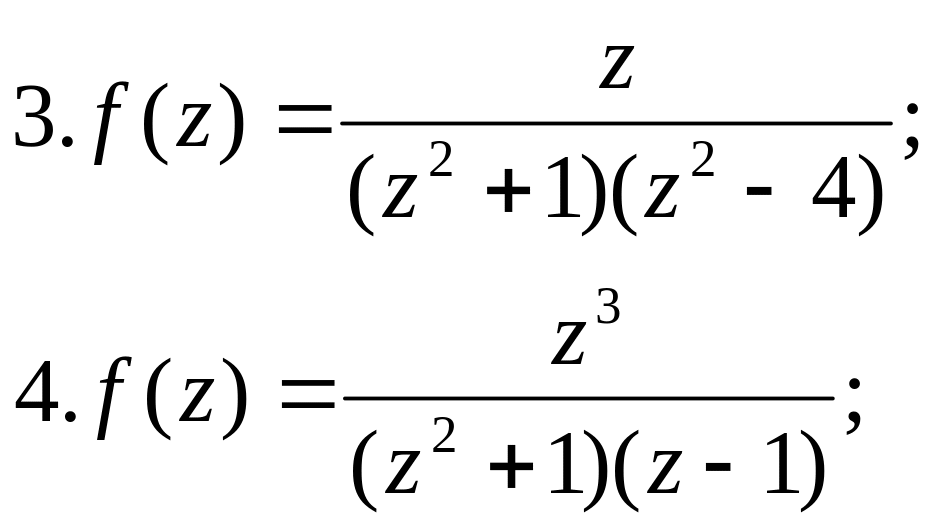- •Змістовний модуль №1. Комплексні числа та їх геометричне представлення
- •Комплексні числа. Форми запису комплексного числа. Дії над комплексними числами
- •1.2. Послідовності і ряди комплексних чисел. Степеневий ряд
- •Змістовний модуль №2. Похідна функції комплексної змінної
- •2.1 Функції із с в с. Границя, неперервність
- •2.2. Похідна функції комплексної змінної. Умови диференційованості
- •2.3. Геометричний зміст модуля і аргументи похідної комплексної функції
- •2.4. Означення аналітичної функції. Поняття Конформного відображення
- •Змістовний модуль №3. Елементарні аналітичні функції
- •Лінійна функція
- •Дробово-лінійна функція
- •Степенева функція. Поверхня Рімана
- •Функція Жуковского
- •Показникова функція комплексної змінної
- •Тригонометричні функції
- •Логарифмічна функція. Точка розгалуження
- •Радикал. Загальна степенева функція
- •Обернені тригонометричні функції
- •Змістовний модуль №4. Інтеграл функції комплексної змінної
- •Інтеграл від функції комплексної зміної по кусочно-гладкому контуру
- •Теорема Коші
- •Невизначений інтеграл. Формула Ньютона-Лейбница
- •Змістовний модуль № 5. Інтегральна формула Коші та її наслідки
- •5.1. Формула Коші. Принцип максимума модуля
- •5.2. Цілі функції. Теорема Ліувіля. Основна теорема алгебри
- •5.3. Розкладання функції в ряд Тейлора. Оцінка коефіцієнтів степеневого ряду
- •5.4. Нулі аналітичної функції. Ізольованість нулів. Теорема єдиності
- •5.5. Аналітичне продовження. Елементарні функції як аналітичні продовження
- •Змістовний модуль № 6. Ізольовані особливі точки аналітичних функцій
- •6.1. Розкладання аналітичної функції в ряд Лорана
- •6.2. Класифікація ізольованих особливих точок. Нескінченно віддалена особлива точка. Критерій особливої точки, яка усувається
- •6.3. Критерій полюса
- •6.4. Теорема Сохоцького-Вейєрштрасса
- •6.5. Раціональні і міроморфні функції
- •Змістовний модуль № 7. Лишки та їх застосування
- •7.1. Означення ЛишкА. Обчислення лишків
- •7.2. Основна теорема теорії лишків
- •7.3. Застосування теореми лишків до обчислення визначених інтегралів
- •Контрольні роботи Контрольна робота №1 (денна форма навчання)
- •Контрольна робота №2 (денна форма навчання)
- •Контрольна робота (заочна форма навчання)
- •Зразки розв'язування задач
- •Література
Невизначений інтеграл. Формула Ньютона-Лейбница
Нехай
функція
аналітична в області D,
тоді розглянемо функцію
 – інтеграл не залежить від шляху
інтегрування, який з’єднує точки z
та
(в силу теореми Коші).
– інтеграл не залежить від шляху
інтегрування, який з’єднує точки z
та
(в силу теореми Коші).
Теорема4.
Нехай
визначена та неперервна у однозв’язній
області
D,
а інтеграл від неї по будь-якому замкнутому
контуру
![]() D
дорівнює нулю, тоді
D
дорівнює нулю, тоді
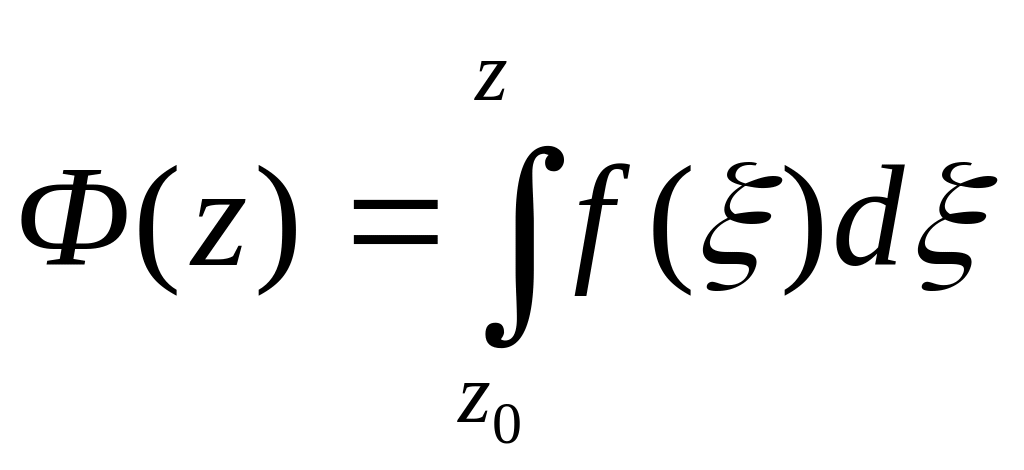
(z,
![]() )
є аналітичною функцією в D
та
)
є аналітичною функцією в D
та
![]() .
.
Доведення: див. [1, с.44].
Помітимо, що для аналітичної умови теореми виконані.
Зауваження.
В умовах теореми
![]() –
первісна до функції
,
тоді в силу теореми не важко отримати
формулу типу Ньютона-Лейбніца.
–
первісна до функції
,
тоді в силу теореми не важко отримати
формулу типу Ньютона-Лейбніца.
У межах умов, вказаних у теремі справедлива формула
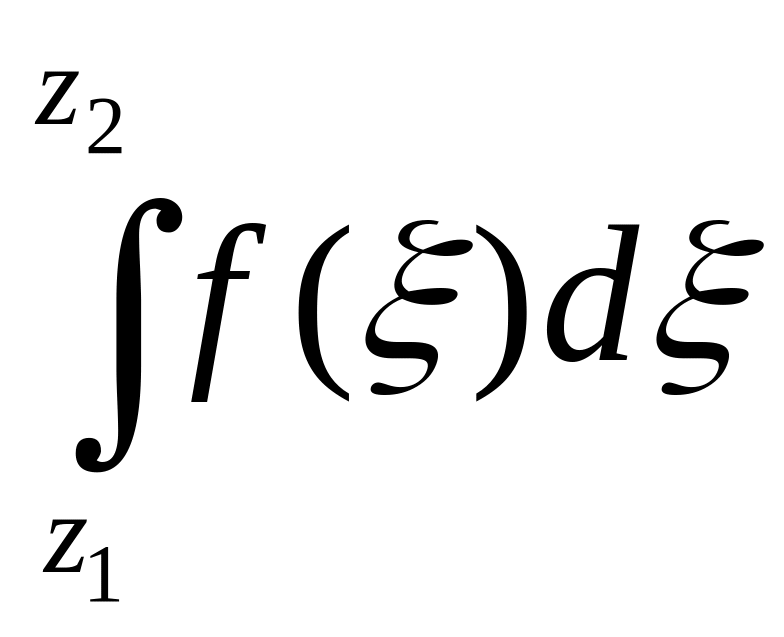 =
=![]() ,
,
де
![]() – довільна первісна функції
– довільна первісна функції
![]() на області D.
на області D.
Приклад1.
Обчислити
![]() .
.
Розв’язання.
Оскільки
![]() –
аналітична на всій площині z,
а
–
аналітична на всій площині z,
а
![]() –
первісна, то
–
первісна, то
=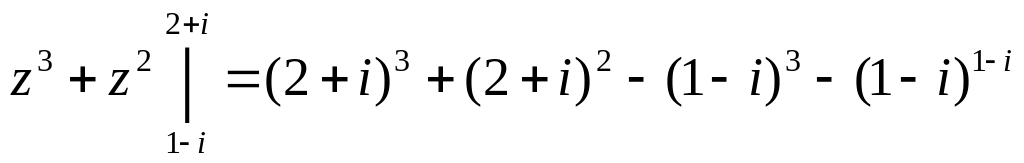 .
.
Вправи
Обчислити:
1)
![]() ,
AB
– шлях, який з’єднує точки
,
AB
– шлях, який з’єднує точки
![]() ;
;
2)
![]() ;
;
3)
![]() – еліпс
– еліпс
![]() ;
;
4)
![]()
![]() АВ
з’єднує точки 1,
і;
АВ
з’єднує точки 1,
і;
5)
![]() –
еліпс
–
еліпс
![]() ;
;
6)
![]() –
коло
–
коло
![]() ;
;
7)
![]() АВ
– з’єднує точки
АВ
– з’єднує точки
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10
![]() ,
,
![]() .
.
Змістовний модуль № 5. Інтегральна формула Коші та її наслідки
5.1. Формула Коші. Принцип максимума модуля
Теорема1.
Нехай функція
– аналітична в однозв’язній області
D.
Тоді для будь-якої точки
![]() і для будь-якого замкнутого кусково-гладкого
контуру
і для будь-якого замкнутого кусково-гладкого
контуру
![]() ,
який цілком лежить в області
,
який цілком лежить в області
![]() та містить точку
всередині себе, виконується рівність
та містить точку
всередині себе, виконується рівність
![]() ,
,
де інтегрування виконується у додатному напрямку замкнутого контуру .
Доведення: див. [2, с.215], [1, с.46], [3, с. 169].
Наслідок. Нехай – коло радіусу R з центром , тоді використовуючи формули Коші можна отримати теорему, яка уточнює відому теорему Вейєрштрасса у випадку аналітичної функції.
Теорема2
(принцип максимуму модуля аналітичної
функції).
Нехай
функція
,
тотожно не рівна постійній, є аналітичною
в області D
і є неперервною в замкненій області
![]() .
Тоді максимальне значення
.
Тоді максимальне значення
![]() досягається тільки на границі області
досягається тільки на границі області
![]() .
.
Доведення стор.220, 201 [3], 49[1].
Крім цього, має місце теорема:
Теорема3.
Нехай
аналітична в області
та неперервна в
![]() .
Тоді у внутрішніх точках області
існує похідна
.
Тоді у внутрішніх точках області
існує похідна
![]() будь-якого порядку, причому має місце
наступна формула
будь-якого порядку, причому має місце
наступна формула
![]() ,
де Г – границя області
.
,
де Г – границя області
.
Доведення див. [2, с. 222-223].
Приклад.
Знайти
![]() ,
,
![]() .
.
Розв’язання.
Розглянемо функцію
![]() ,
тоді інтеграл
,
тоді інтеграл
 по формулі Коші (
по формулі Коші (![]() знаходиться в середині контуру
знаходиться в середині контуру
![]() ) дорівнює
) дорівнює
![]() .
.
Вправи
Обчислити
|
|
5.2. Цілі функції. Теорема Ліувіля. Основна теорема алгебри
Означення1. Аналітична на всій комплексній площині функція називається цілою функцією.
Теорема4 (Ліувіля). Нехай – ціла функція, а її модуль обмежений, тоді ця функція – константа.
Доведення [3, с.173], [2, с.225].
Приклад1.
![]() -
ціла функція і
-
ціла функція і
![]() ,
отже
,
отже
![]() -
необмежений, тобто існує z такий, що
-
необмежений, тобто існує z такий, що
![]() .
.
Застосування теореми Ліувіля є основною теоремою алгебри:
Всякий
многочлен
![]() має хоча б один нуль.
має хоча б один нуль.
Доведення
слідує з того, що якщо нулів немає, то
функція
![]()
має обмежений модуль і є цілою, не буде константою. Це протиречить теоремі Ліувіля. Отже, припущення щодо відсутності нуля – невірне.
5.3. Розкладання функції в ряд Тейлора. Оцінка коефіцієнтів степеневого ряду
Теорема5.
Функція
,
аналітична в середині кола
![]() розкладається в цьому колі в степеневий
ряд:
розкладається в цьому колі в степеневий
ряд:
![]() .
.
Коефіцієнти
![]() визначаються по формулі
визначаються по формулі
![]() або
або
![]() ,
де l
- будь-який кусочно-гладкий замкнений
контур, який повністю належить колу та
знаходиться навколо точки
.
Ряд визначений однозначно.
,
де l
- будь-який кусочно-гладкий замкнений
контур, який повністю належить колу та
знаходиться навколо точки
.
Ряд визначений однозначно.
Доведення теореми див. [2, с.225], [1,с.64].
Нехай
аналітична в колі
.
Приймемо за
![]() -
будь-яка окружність з центром в точці
,
що цілком лежить в колі
,
і через
-
будь-яка окружність з центром в точці
,
що цілком лежить в колі
,
і через
![]() -
максимум модуля
на колі
,
тоді для коефіцієнтів ряду Тейлора
вірна оцінка
-
максимум модуля
на колі
,
тоді для коефіцієнтів ряду Тейлора
вірна оцінка
![]() ,
,
які носять назву нерівність Коші.
Приклад1.
Розкласти в ряд
![]() для
для
![]() .
.
Розв’язання. ![]()
![]()
Вправи
Розкласти в ряд Тейлора в =0 функції:
|
|