2.4. Означення аналітичної функції. Поняття Конформного відображення

Означення9. Функція диференційована в кожній точці області називається аналітичною в області .

Означення10. Функція називається аналітичною в точці , якщо вона аналітична в деякому околі точки .

З властивостей похідної слідує, що справедливі твердження:

1) якщо , аналітичні в , то – аналітична всюди, де ;

2) якщо в аналітична, а аналітична в області, що є образом при відображенні , то функція аналітична в :

3) якщо аналітична в і , , то в області значень функції визначена обернена функція – аналітична в , причому .

Наприклад, – аналітична ( ) у всій площині окрім точки , 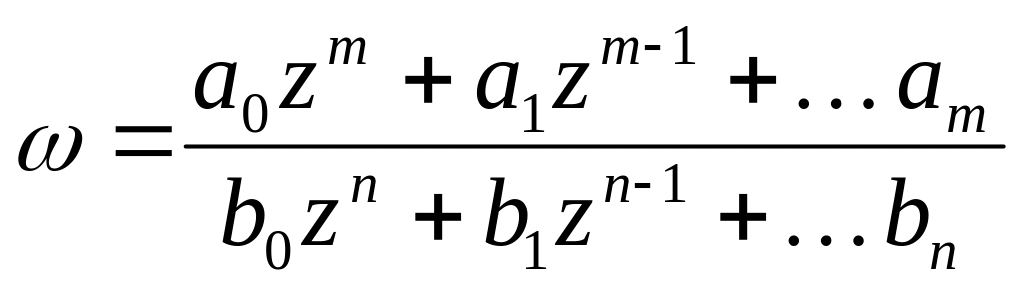– аналітична функція окрім точок , в яких знаменник перетворюється в нуль.

Нехай відображає площину z у площину . Розглянемо на площині z дві довільні гладкі криві , які перетинаються у точці .

Якщо при відображенні криві переходять у криві відповідно ( перетинаються у точці ), кути між кривими у точці та кривими у рівні, то кажуть, що відображення у точці має властивість збереження кутів.

Нехай відображення площини z у площину . Розглянемо у площині z трикутник з вершиною в точці та довільними нескінченно малими лінійними елементами , , які виходять з . Якщо при відображенні він переходе у трикутник з вершиною в точці , який подібний вихідному, з точністю до нескінченно малої більш високого порядку, ніж сторони вихідного трикутника, то кажуть, що відображення в точці має властивість постійності розтягування.

Означення11. Взаємнооднозначне відображення області комплексної площини z на область D комплексної площини називається конформним, якщо це відображення у всіх точках z має властивість збереження кутів і постійності розтягування.

Якщо кути при відображені не змінюють направлень, то кажуть про конформне відображення І-го роду. Якщо кути змінюють направлення на протилежні, то кажуть про конформне відображення ІІ-го роду.

Крім того, кажуть, що відображення конформне у нескінченно віддаленій точці, якщо відображає початок z=0 конформно у площину .

Теорема3. Для того, щоб функція реалізувала конформне відображення І-го роду області , необхідно і достатньо, щоб в цій області функція була:

1. однолистою;

2. аналітичною;

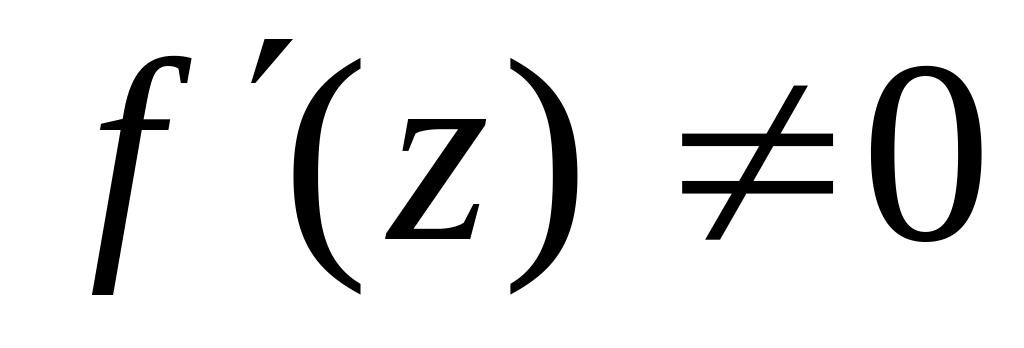3. для будь-якого z ;

Доведення: див. [2, с. 107], [1, 146].

Приклад 1. відображає площину z на конформно, бо .

Приклад 2. дзеркальне відображення відносно осі Ox, змінює напрям кутів на протилежний. Таким чином – конформне відображення ІІ-го роду (хоча функція не аналітична!)

Вправи

Знайти точки, в яких відображення конформне (І-го роду).

1) ;

2) ;

3) ;

4) .

Чи конформні відображення у нескінченно віддаленій точці

5) ;

6) ;

7) ;

8) .

Покажіть, що відображення здійснюють конформне відображення ІІ-го роду

9) ;

10) , задовольняє теоремі.

Змістовний модуль №3. Елементарні аналітичні функції

1. Лінійна функція

Означення1. Функція виду (a≠0) називається лінійною.

Функція визначена та однозначна для будь-якого z та оскільки z , то вона здійснює конформне відображення площини z на площину .

При цьому відображенні у всіх точках z дотична до довільної кривої, яка проходить через z, повертається на один і той самий кут і розтягує площину z у всіх точках на .

Якщо a=1, то , і розтягування та поворот відсутні, тобто функція зміщує площину на вектор .

Якщо a 1, то можна представити , де , тобто кожен вектор (який виходить з ) повертаючись на та розтягує у разів переходе у вектор .

Таким чином ( ), повертає площину z на кут та розтягує у разів відносно точки .

Приклад1. .

, .

Площина z повертається на кут та розтягується у разів відносно точки –2.

Вправи

Знайти лінійні відображення:

1. яке відображує трикутник з вершинами 0,1, і на подібний трикутник 0,2, 1+і.

2. з нерухомою точкою 1+2і, яке переводе точку і у b-i .

3. яке переводе верхню півплощину на себе.

4. яке переводе верхню півплощину на нижню півплощину.

5. яке переводе верхню півплощину на праву півплощину.

6. яке переводе праву півплощину на себе.

7. яке переводе праву півплощину на ліву.

8. яке переводе смугу 0<x<1 на себе.

9. яке переводе смугу 2<y<1 на себе.

10. яке переводе смугу, яка обмежена прямими y=x, y=x–1 на себе.