Зразки розв'язування задач

Задача № 1. Знайти всі значення , їх модуль та аргумент.

Розв'язання. Означення комплексного степеня: (*), де а 0 і b – довільні комплексні числа.

Звертаємо увагу на те, що у правій частині (*) визначено незалежно від вищенаведеного означення степеня (інакше був би «круг в означенні»). А саме: є значення показникової функції при , яка означена як сума степеневого ряду 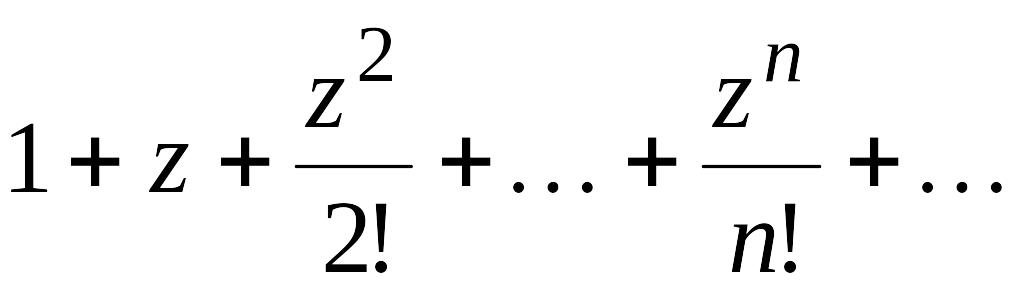в який входять лише цілі невід'ємні степені z (дія множення). У даному випадку .

Маємо за означенням (*) і далі за означенням комплексного логарифма:

(**)

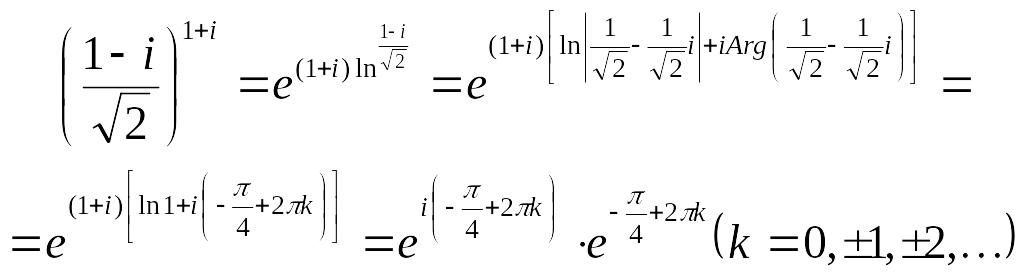Застосувавши до першого множника в (**) формулу Ейлера, матимемо:

.

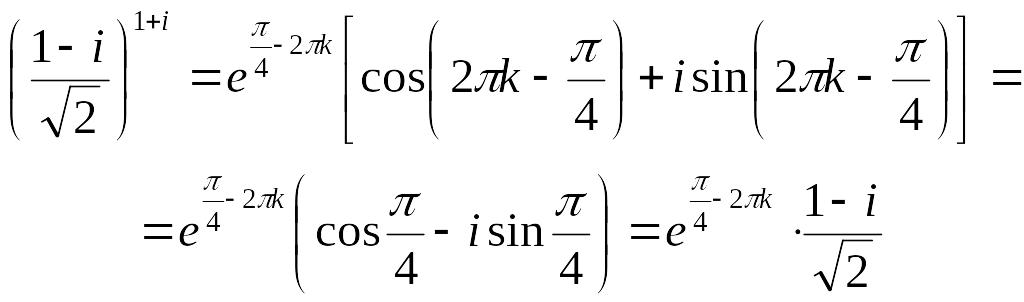Порівнюючи (**) з загальною показниковою формою комплексного числа , одержимо:

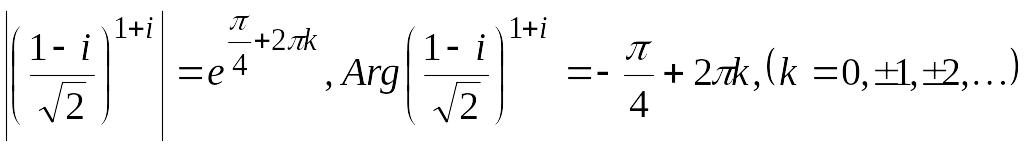
Задача № 2. Перевірити умови Даламбера – Ейлера для функції і визначити, в яких точках до є диференційовна функція.

Розв'язання. Хай . Тоді рівняння Даламбера – Ейлера мають вигляд:

.

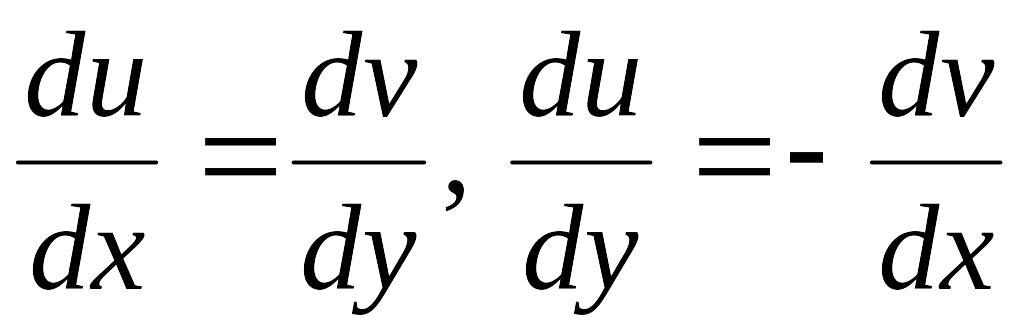Відокремимо дійсну і уявну частини функції до:

.

Отже,

.

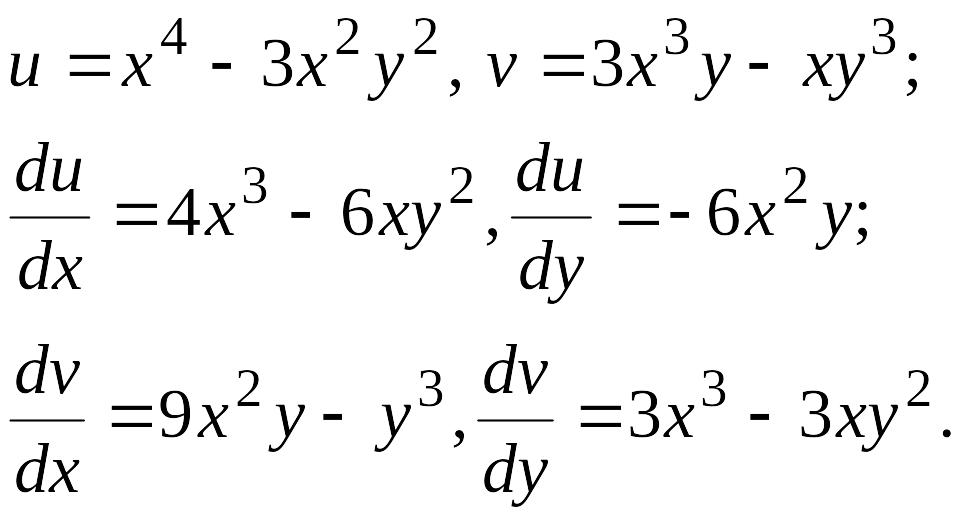Рівності

(*)

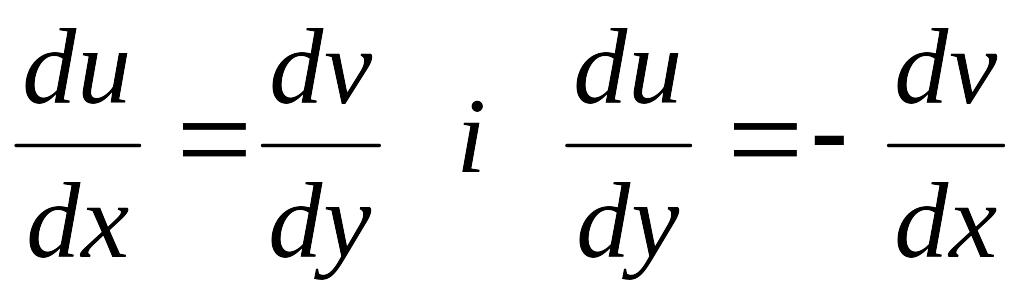очевидно виконуються в точці . Зовсім легко переконатись, що ця точка є єдиною, в якій задовольняються рівняння Даламбера – Ейлера.

Справді, перше рівняння системи (*) : при рівносильне рівнянню , друге рівняння (*) при рівносильне рівнянню . А система х²=Зу², Зх²=у² не має жодного розв'язку, крім х=0, у=0.

Беручи до уваги, що функції u і v є всюди диференційовними, приходимо до висновку, що функція до є диференційовна в точці (достатність умов Даламбера – Ейлера для диференційовності функції) і лише в цій точці (необхідність цих же умов).

Задача № 3. Знайти аналітичну функцію аргумента , уявна частина якої (1)

Розв'язання. Оскільки є функція аналітична, для неї справджуються рівняння Даламбера – Ейлера, тобто:

Залишається з цих рівнянь визначити и. Скористаємось першим рівнянням Даламбера – Ейлера. Беручи до уваги (1), маємо:

;

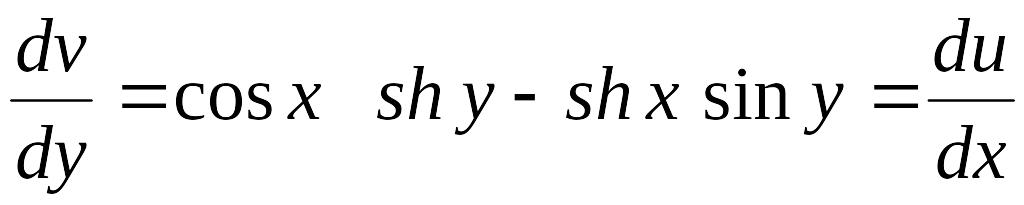Звідси

(тут замість сталої С при знаходженні первісної функції и пишемо , оскільки у при знаходженні похідної і обчисленні інтеграла вважається за сталу, отже, взагалі кажучи, входить в С).

Далі, інтегруючи, одержуємо:

(2)

Використаємо тепер друге рівняння Даламбера – Ейлера для знаходження .

Для цього спочатку знайдемо з (2) і з (1).

;

Але 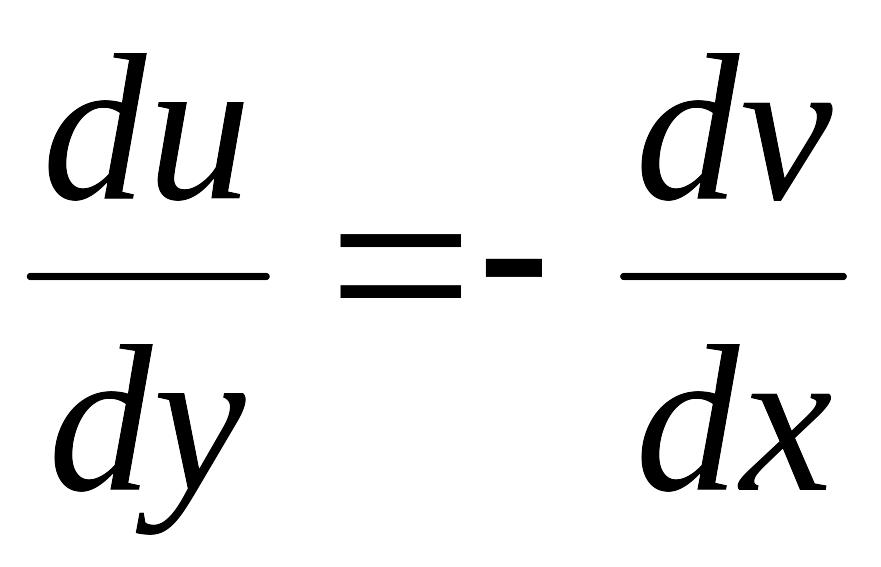, тобто: ;

Звідки , ;

(С – дійсна довільна стала).

Отже, (3)

Виразимо тепер праву частину (3) через z. Оскільки, дістаємо:

.

Задача № 4. Визначити область збіжності функціонального ряду

Розв'язання. Застосуємо ознаку збіжності рядів Даламбера, яка, як відомо, має силу і в комплексній області звичайно для ряду модулів.

Маємо:

Отже, за ознакою Даламбера ряд буде збіжним (і до того абсолютно) при всіх z таких, що ;

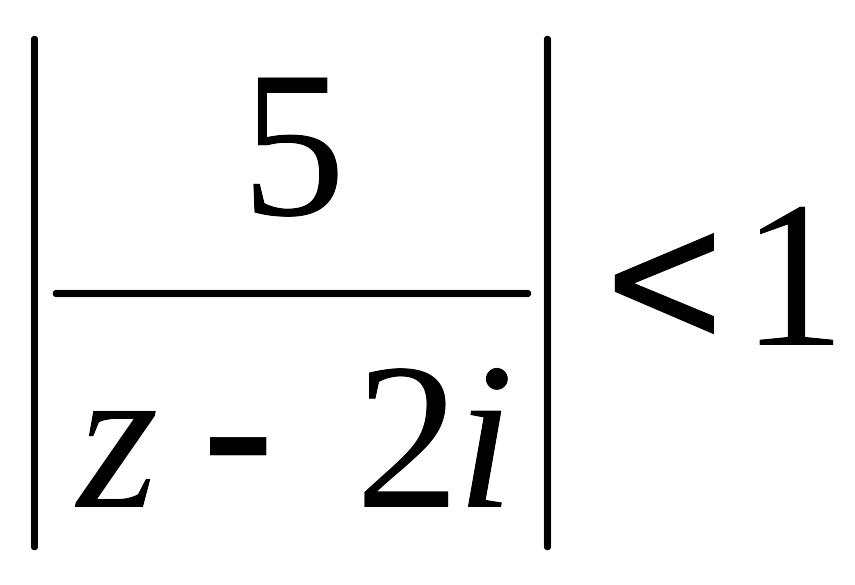Тобто .

Якщо , то ,

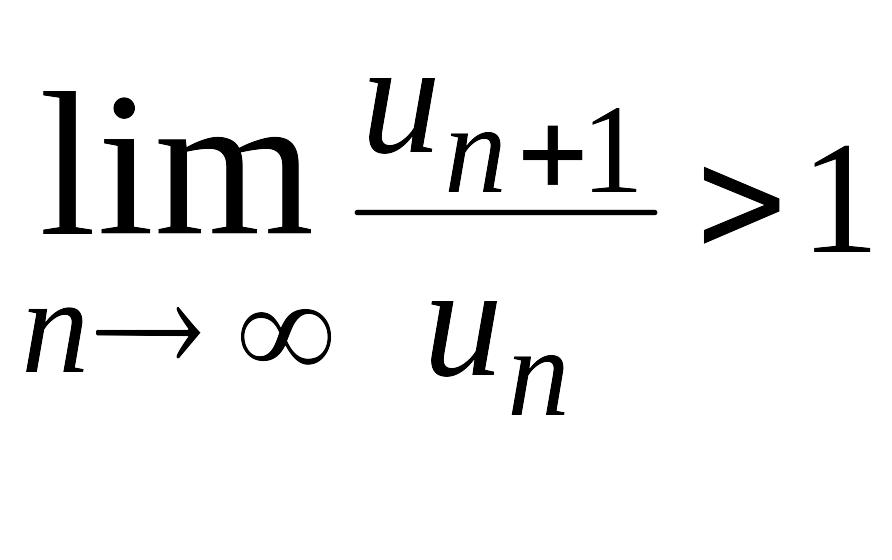Звідки , і даний ряд буде розбіжним, оскільки не виконується навіть необхідна умова збіжності.

Залишається дослідити збіжність ряду при . При цій умові маємо . Ряд 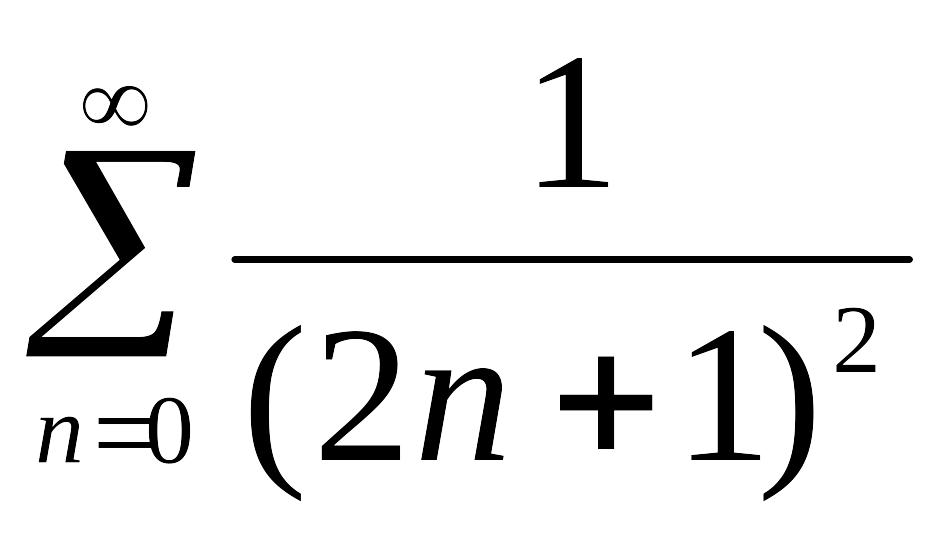, як легко встановлюється за інтегральною ознакою збіжності, є збіжний. Справді, невласний інтеграл 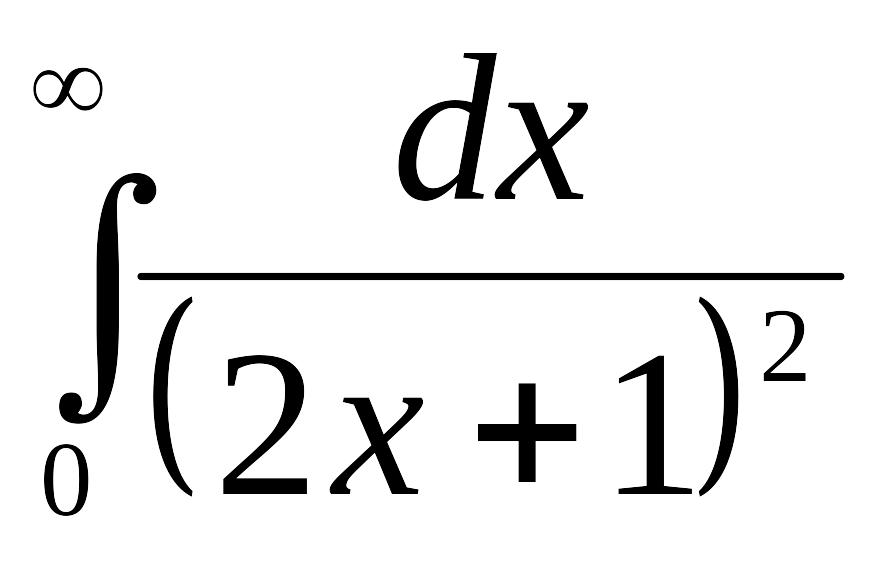існує:

.

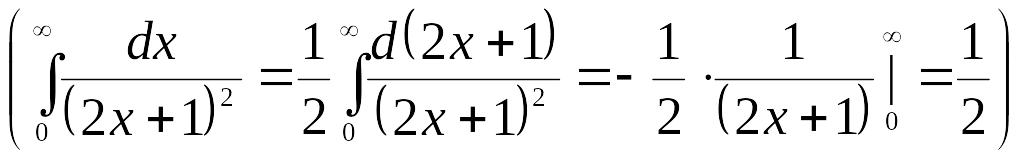1

2х +

Таким чином, область абсолютної збіжності заданого ряду є вся зовнішність круга з центром в точці і радіусом, рівним 5, причому коло цього круга включається в область збіжності.

Задача № 5. Розкласти в ряд Тейлора за степенями функцію 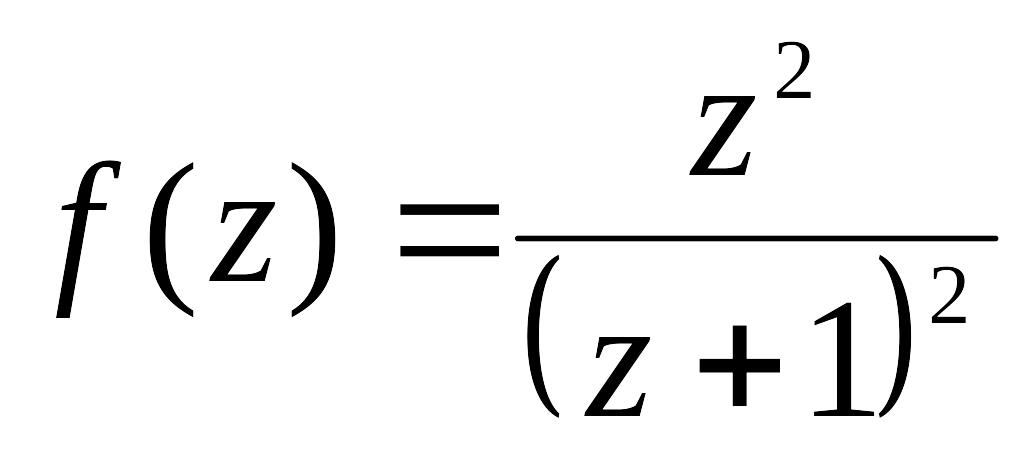і визначити радіус збіжності.

Розв'язання. Функція є аналітична в усій комплексній площині, за винятком точки , отже, її можна розкласти в ряд Тейлора в крузі з центром і радіусом, рівним віддалі від точки до найближчої особливої точки: , звідси радіус круга збіжності з центром в точці є рівний 2. Безпосередній розклад в ряд Тейлора по формулі:

веде до складних обчислень. Використаємо інший спосіб:

. (*)

Представимо як суму спадної геометричної прогресії:

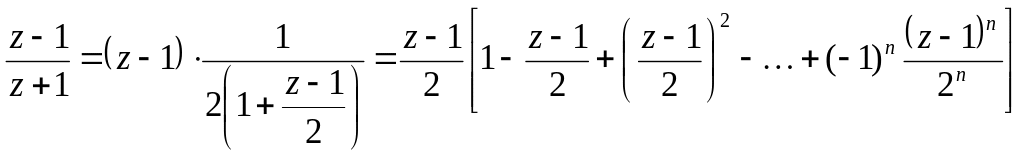
Отже, при .

Що ж до другого доданка (*) , то він являє собою похідну по z від .

Аналогічно попередньому розкладемо в ряд Тейлора за степенями і про диференціюємо цей степеневий ряд почленно ( адже степеневі ряди почленно диференціювати в крузі збіжності):

_{При .}

Нарешті:

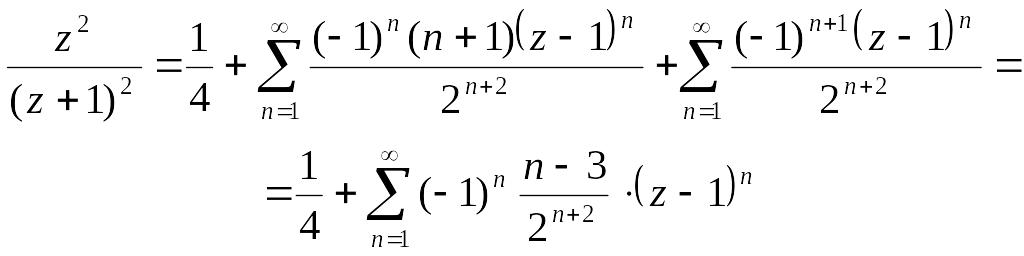
_{В крузі} .

З теореми єдиності розкладу функції в ряд Тейлора випли­ває, що одержаний степеневий ряд і є рядом Тейлора функції;

в крузі .

З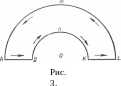 адача № 6. Обчислити інтеграл , де С – границя півкільця, обмеженого верхніми півколами |z|=1, |z|=2 і відрізками осі абсцис від точки —2 до точки – 1, та від точки 1 до точки 2.

Інтегрування проводиться в додатному напрямі (див. рис. 3).

Розв’язання. Перетворимо підінтегральний вираз, помноживши чисельник і знаменник на z:

.

.

На колі я маємо: , аналогічно на другому колі

Отже,

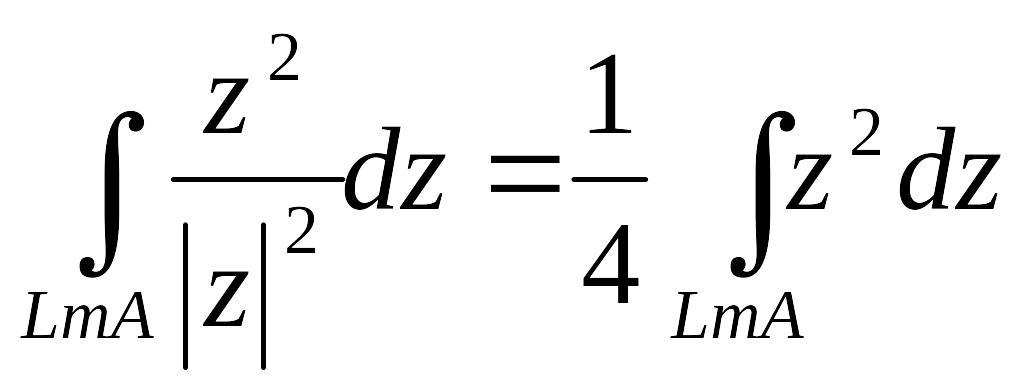
Оскільки підінтегральна функція є аналітична в будь-якій області, останній інтеграл можна обчислити за формулою Ньютона – Лейбніца:

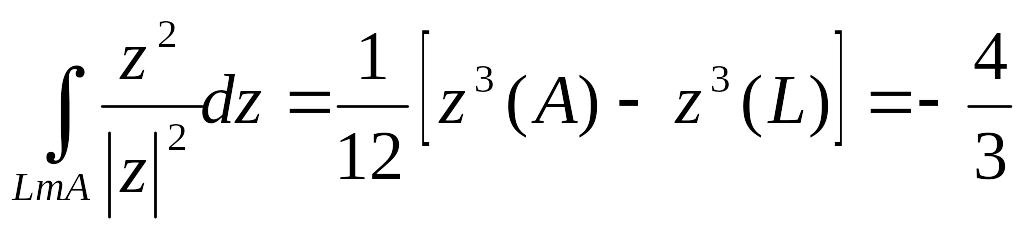
Аналогічно,

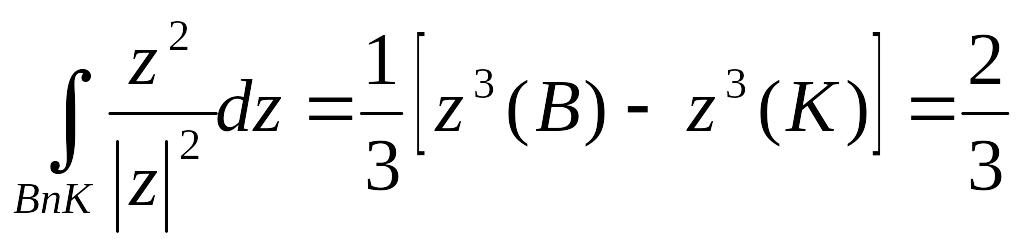
Далі на відрізку АВ , оскільки тут z є дійсним від'ємним числом, а на відрізку KL . В обох випадках , тому

і

Остаточно:

Задача № 7. Обчислити за допомогою інтегральної формули Коші інтеграл

Розв'язання. Підінтегральна функція є аналітична в крузі , крім точки , бо всі інші нулі знаменника: –1, і, – і знаходяться поза цим кругом.

Справді, визначимо віддаль між центром круга а та точкою і, тобто . Маємо (адже а – дійсне число). Крім цього, , тобто , чим і встановлено, що точка і знаходиться поза колом . Далі ; , отже, точки – і та – 1 теж знаходяться поза даним колом.

Представимо тепер розглядуваний інтеграл у вигляді

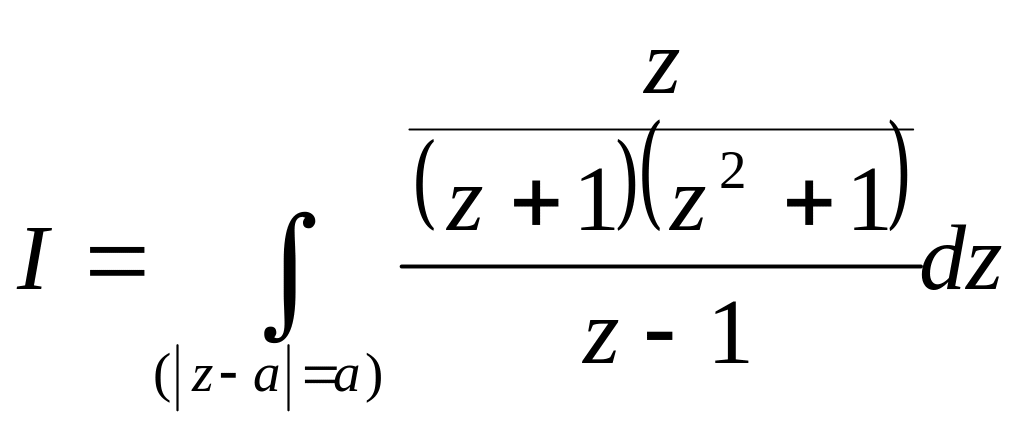
Оскільки функція аналітична всередині С і на самому колі С, то можна до інтеграла (*) застосувати інтегральну формулу Коші:

де за приймемо , а за .

Тоді .

Задача № 8. Розкласти в ряд Лорана в околі точки функцію .

Розв'язання. Функція не є аналітичною в точці , отже, вона не розкладається в околі цієї точки в ряд Тейлора. Але цю функцію можна розкласти в околі точки в ряд Лорана, тобто в «двосторонній степеневий» ряд. за степенями , оскільки область, в якій вона є аналітична (вся комплексна площина з вилученою точкою ), можна розглядати як кругове кільце з центром в точці , де внутрішній радіус , зовнішній –

Щоб розкласти функцію в ряд Лорана за степенями , спочатку перетворимо її тотожно:

, де .

Використаємо відомий ряд для :

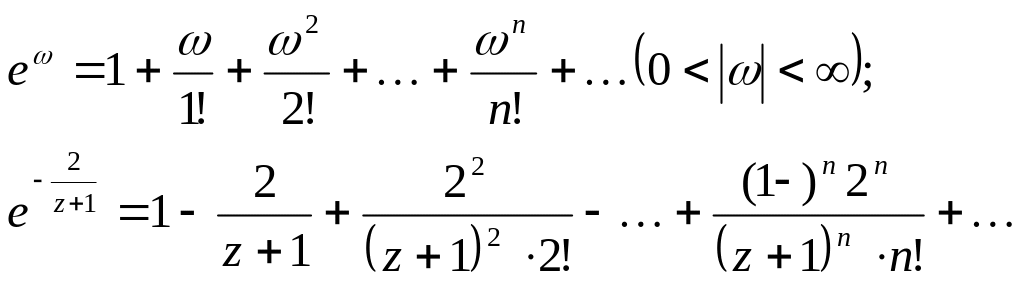
Є'

Нарешті:

Цей розклад справедливий в усій комплексній площині, з якої вилучена точка .

Задача № 9. Розкласти в ряд Лорана функцію в околі нескінченно віддаленої точки.

Розв'язання. Покладемо ; тоді функцію розкладемо в ряд Тейлора в околі точки . Для цього розкладемо на елементарні дроби: .

Кожний із доданків у виразі в дужках представимо як суму спадної геометричної прогресії, а саме:

1 — 2/2

1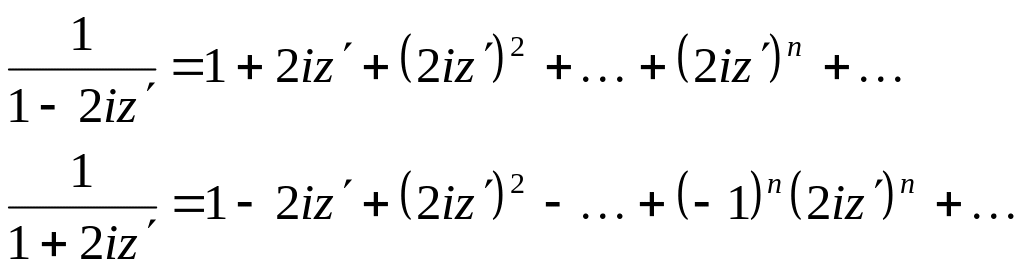

причому обидва розклади мають місце при (інак­ше прогресії не будуть спадними). Таким чином:

причому цей розклад справедливий у зовнішності круга (адже і ).

Задача № 10. Обчислити за допомогою теореми про лишки інтеграл , де С- коло , n – ціле число.

Розв'язання. Контур інтегрування С є коло з центром в точці та радіусом r. Якщо , то функція є аналітична в області, обмеженій контуром С, і на самому контурі, оскільки точка знаходиться поза контуром. Отже, за теоремою Коші – Гурса .

Якщо , то точка , яка є єдиною особливою точкою підінтегральної функції, знаходиться в області, об­меженій контуром С. Тоді за основною теоремою про лишки

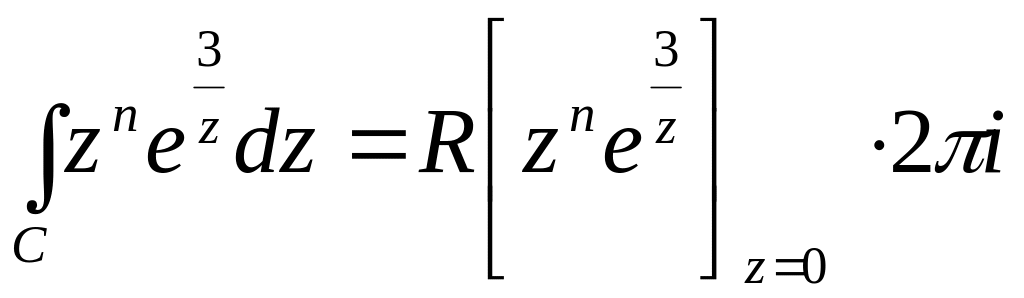
Обчислимо лишок підінтегральної функції в точці . Для цього розкладемо її в ряд Лорана в околі цієї точки. Маємо:

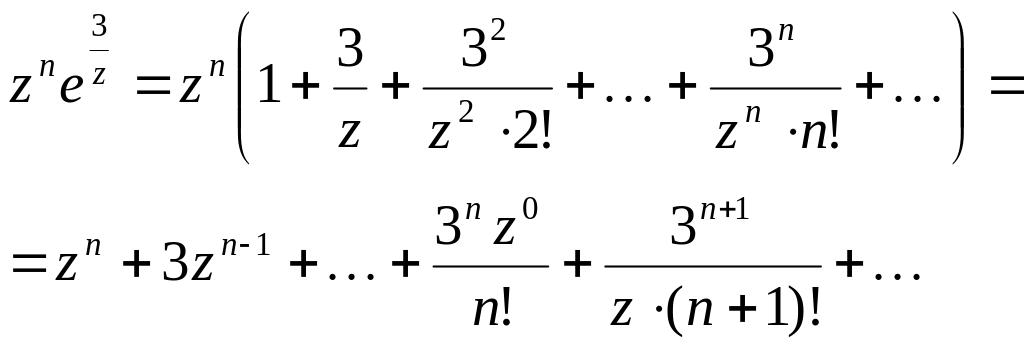
тепер, якщо , то лишок функції, який за означенням рівний коефіцієнту при в лорановому розкладі, буде . Якщо ж , то в наведеному розкладі в ряд Лорана не буде члена з (наприклад, при n = – 2 розклад матиме вигляд .). Отже, в цьому випадку.

А тому тоді .

Остаточно маємо:

(Нагадуємо, що 0! за означенням рівний 1).

Задача № 11. Довести, що функція відображає конформно верхній півкруг на перший квадрант.

Розв'язання. Функція є дробово-лінійна, отже, вона перетворює коло на коло або на пряму в си­лу кругової властивості дробово-лінійних перетворень. Оскільки точка z=1, яка лежить на колі , перетво­рюється на площині в нескінченно віддалену точку, образом кола буде пряма (коло нескінченно великого радіуса). Аналогічно і образом дійсної осі у=0 теж буде пряма.

Точки кола відповідно перетворяться в точки відповідно перетворюється в точки

Отже, образом кола на площині буде уявна вісь.

Аналогічно точки дійсної осі площини відобразяться відповідно у точки , і образ дійсної осі площини Г являтиме дійсну вісь площини .Позначивши , одержимо:

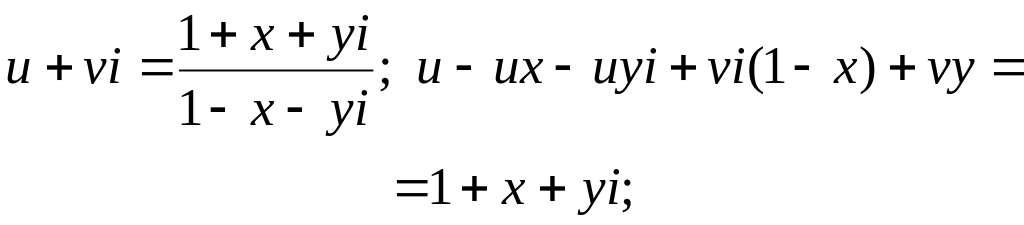
прирівнюючи дійсні і уявні частини в обох частинах рів­ності, одержимо:

Оскільки для всіх точок всередині круга , то и>0, до того на верхньому півкрузі у>0, тому .

Таким чином, верхній півкруг площини відображається на перший квадрант площини .