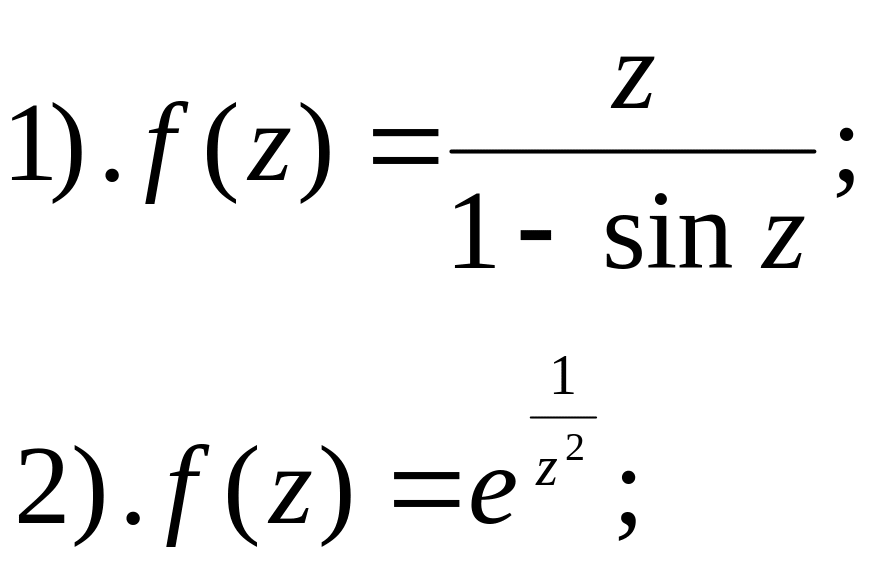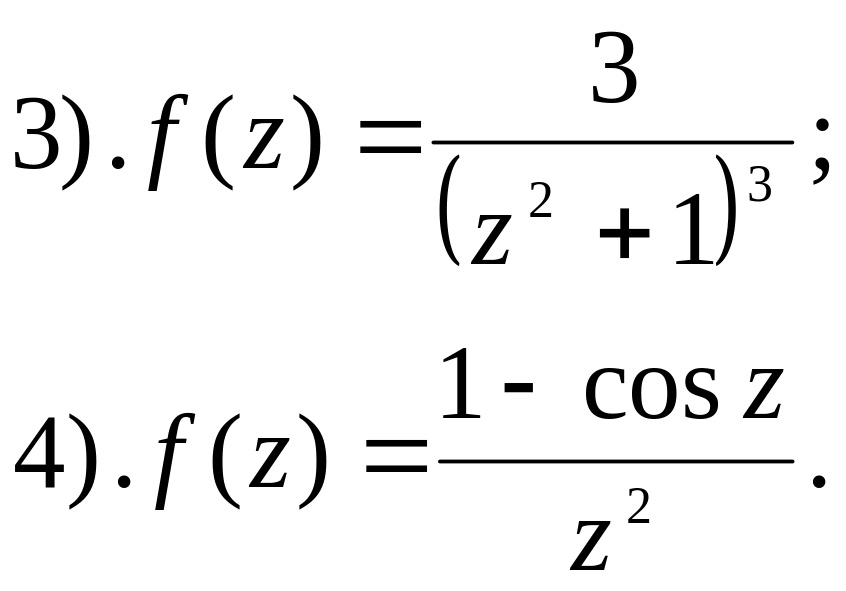6.2. Класифікація ізольованих особливих точок. Нескінченно віддалена особлива точка. Критерій особливої точки, яка усувається

Означення1. Нехай називається ізольованою особливою точкою - якщо аналітична функція в кільці , а - особлива точка (тобто в не є аналітичною).

В кільці розкладається в ряд Лорана; отримаємо один з трьох випадків:

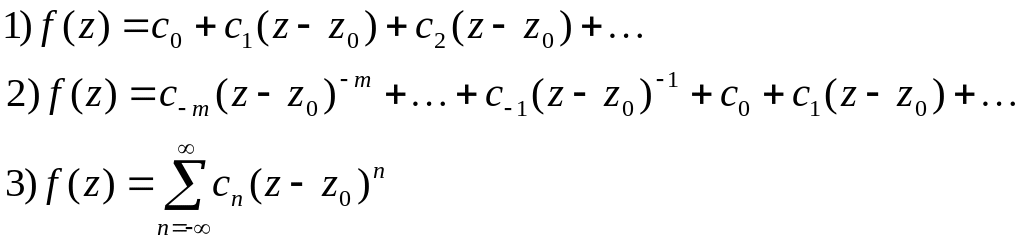
У першому випадку називається особливою точкою, яка усувається.

У другому випадку називається полюсом порядку m.

У третьому випадку називається істотною особливою точкою.

Теорема2. Нехай особлива точка , яка усувається, тоді існує скінчений

Таким чином, можна довизначити в точці значенням і вона буде аналітичною в колі .

Теорема3. Якщо аналітична в та обмежена, то - особлива точка , яка усувається.

Доведення теореми див. [1, с.212], [2, с. 289].

Нехай аналітична в деякому околі нескінченно віддаленої точки . Припустимо, що при цьому , перейде в . Функція аналітична в околі . Нехай розклад в ряд Лорана в околі має вигляд . Повертаючись до змінної , маємо

1. Якщо в отриманому розкладі немає членів з додатними степенями, то 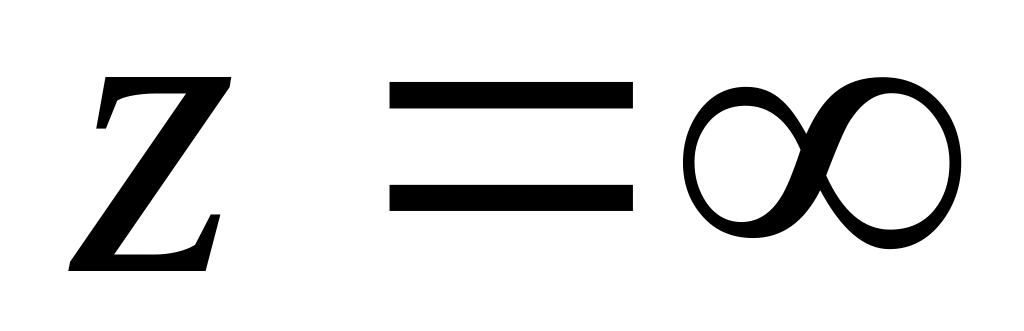- особлива точка, яка усувається.

2. Якщо в розкладі скінчене число членів з додатними степенями, то - полюс.

3. Якщо в розкладі нескінчене число членів з додатними степенями, то - істотно особлива точка.

Приклад1. .

Розв’язання:

– аналітична, крім перша чудова границя. Таким чином, – особлива точка, яка усувається.

6.3. Критерій полюса

Нехай аналітична в .

Теорема4. Для того, щоб було полюсом функції необхідно і достатньо, щоб

Доведення теореми див. [2, с. 293], [1, с. 114].

Зауваження. Якщо – полюс порядку m функції , то її можна представити у вигляді , де і аналітична в колі .

Приклад1. , де – полюси першого порядку, – полюс другого порядку.

Приклад2. . Знайти полюса.

Розв’язання: , т. я. , а . Таким чином, , де в точці - аналітична, отже - полюс другого порядку.

6.4. Теорема Сохоцького-Вейєрштрасса

Нехай – істотна особлива точка функції аналітичної в області .

Теорема5 (Сохоцького-Вейєрштрасса). Яке б не було комплексне число W(скінчене або нескінчене), існує така послідовність , що

.

Доведення теореми див.[2, с.294], [1, с.115].

Приклад1. . Знайти особливі точки.

Розв’язання. – ізольована особлива точка, так як в інших z - аналітична.

, тобто в розкладі в ряд Лорана нескінченно багато від’ємних степеней. Отже, - істотно особлива точка.

Вправи (до пунктів 6.2 – 6.4)

1. Довести, що – особлива точка, яка усувається.

1) 2)

2. Довести, що – полюс.

1) 2)

3. Довести, що – істотно особлива точка.

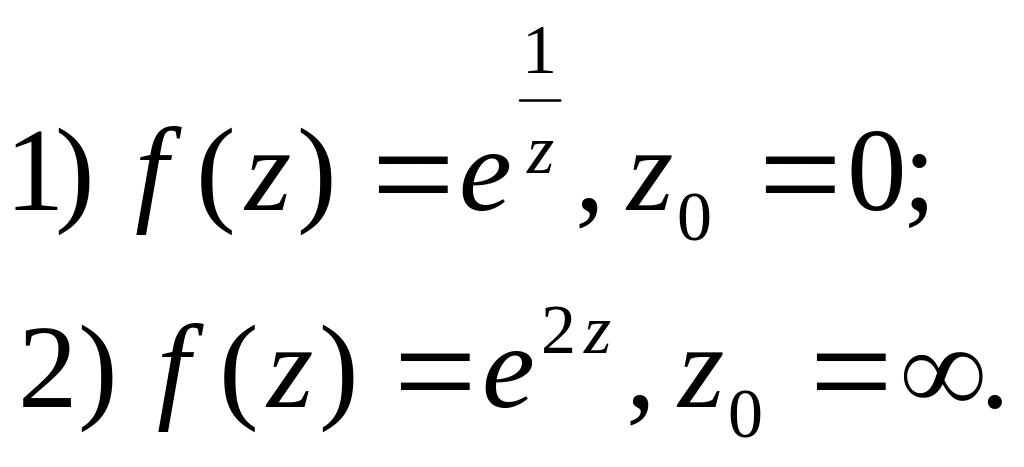
4. Знайти особливі точки.

6.5. Раціональні і міроморфні функції

Означення2. Цілою називається функція , аналітична в усіх точках розширеної площини z, за виключенням нескінченно віддаленої точки.

Якщо полюс порядку m, то має розклад Лорана в у вигляді – ціла раціональна функція степені m.

Якщо істотньо особлива, то – ціла трансцендентна функція.

Означення3. Міроморфною називається така аналітична функція , яка в скінченій частині комплексної площини z не має інших особливих точок, крім полюсів.

Окремими класами міроморфних функцій є цілі та дробово-раціональні функції.

Дробово-раціональна функція – .

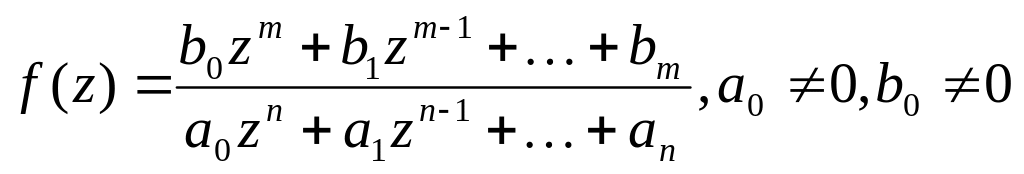Теорема6. Однозначна функція , всі особливості якої в розширеній комплексній площині є полюси, є дробово-раціональною функцією.

Доведення теореми див.[2, с.301].