Міністерство освіти і науки україни

Херсонський державний університет

Факультет фізики, математики та інформатики

Кафедра алгебри, геометрії та математичного аналізу

Самойленко В.Г.

Плоткін Я.Д.

Котова О.В.

Теорія функцій комплексної змінної

Навчально – методичний посібник

для студентів ІV курсу факультету фізики, математики та інформатики

Затверджено

вченою радою ХДУ

Протокол №_____від_____________

Херсон – 2010

Зміст

Змістовний модуль №1. Комплексні числа та їх геометричне представлення 4

1.1. Комплексні числа. Форми запису комплексного числа. Дії над комплексними числами 4

1.2. Послідовності і ряди комплексних чисел. Степеневий ряд 6

Змістовний модуль №2. Похідна функції комплексної змінної 9

2.1 Функції із С в С. Границя, неперервність 9

2.2. Похідна функції комплексної змінної. Умови диференційованості 12

2.3. Геометричний зміст модуля і аргументи похідної комплексної функції 14

2.4. Означення аналітичної функції. Поняття Конформного відображення 16

Змістовний модуль №3. Елементарні аналітичні функції 20

3.1. Лінійна функція 20

3.2. Дробово-лінійна функція 21

3.3. Степенева функція. Поверхня Рімана 24

3.4. Функція Жуковского 26

3.5. Показникова функція комплексної змінної 28

3.6. Тригонометричні функції 29

3.7. Логарифмічна функція. Точка розгалуження 31

3.8. Радикал. Загальна степенева функція 32

3.9. Обернені тригонометричні функції 33

Змістовний модуль №4. Інтеграл функції комплексної змінної 35

4.1. Інтеграл від функції комплексної зміної по кусочно-гладкому контуру 35

4.2. Теорема Коші 37

4.3. Невизначений інтеграл. Формула Ньютона-Лейбница 38

Змістовний модуль № 5. Інтегральна формула Коші та її наслідки 40

5.1. Формула Коші. Принцип максимума модуля 40

5.2. Цілі функції. Теорема Ліувіля. Основна теорема алгебри 41

5.3. Розкладання функції в ряд Тейлора. Оцінка коефіцієнтів степеневого ряду 42

5.4. Нулі аналітичної функції. Ізольованість нулів. Теорема єдиності 43

5.5. Аналітичне продовження. Елементарні функції як аналітичні продовження 44

Змістовний модуль № 6. Ізольовані особливі точки аналітичних функцій 46

6.1. Розкладання аналітичної функції в ряд Лорана 46

6.2. Класифікація ізольованих особливих точок. Нескінченно віддалена особлива точка. Критерій особливої точки, яка усувається 47

6.3. Критерій полюса 48

6.4. Теорема Сохоцького-Вейєрштрасса 49

6.5. Раціональні і міроморфні функції 50

Змістовний модуль № 7. Лишки та їх застосування 51

7.1. Означення ЛишкА. Обчислення лишків 51

7.2. Основна теорема теорії лишків 52

7.3. Застосування теореми лишків до обчислення визначених інтегралів 53

Контрольні роботи 56

Контрольна робота №1 (денна форма навчання) 56

Контрольна робота №2 (денна форма навчання) 69

Контрольна робота (заочна форма навчання) 82

Зразки розв'язування задач 88

Література 98

Змістовний модуль №1. Комплексні числа та їх геометричне представлення

1. Комплексні числа. Форми запису комплексного числа. Дії над комплексними числами

Комплексні числа складають клас математичних об’єктів, які визначаються описаними нижче властивостями.

Кожному комплексному числу можна поставити у відповідність єдину упорядковану пару дійсних чисел та і навпаки.

Сума і добуток двох комплексних чисел і визначаються відповідно і .

Дійсні числа – комплексні числа . Уявна одиниця , визначається , тоді , тобто дійсне число . Тому кожне комплексне число може бути записане у вигляді суми дійсного числа і чисто уявного числа . Така форма запису називається алгебраїчною, при цьому – дійсна частина , – уявна частина .

Геометрично комплексне число можна інтерпретувати, як точку площини з декартовими координатами , або вектор площини з координатами .

З цього легко випливає тригонометрична форма запису комплексного числа , де , і називається модулем комплексного числа .

;

і називається головним значенням аргументу комплексного числа .

Так як кожній точці на комплексній площині можна поставити у відповідність безліч значень аргументу, які відрізняються на , то

.

Крім того, використовуючи формулу Ейлера , отримуємо показникову форму запису комплексного числа .

Використовуючи різні форми запису комплексних чисел, отримуємо результати дій над числами.

;

, .

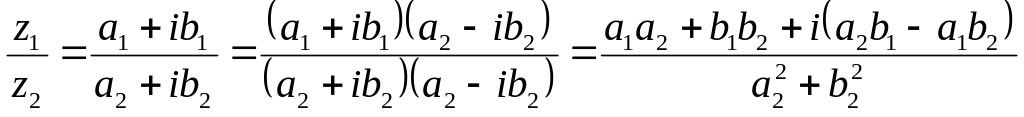
Більш детальне викладення цього матеріалу див. [1, 2, 3].

Приклад 1.

Обчислити .

Розв’язання. , ,

.

, .

,

,

,

, .

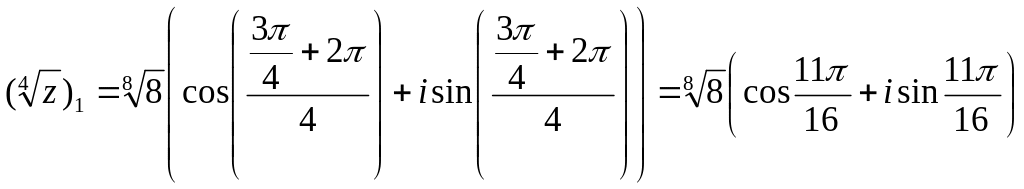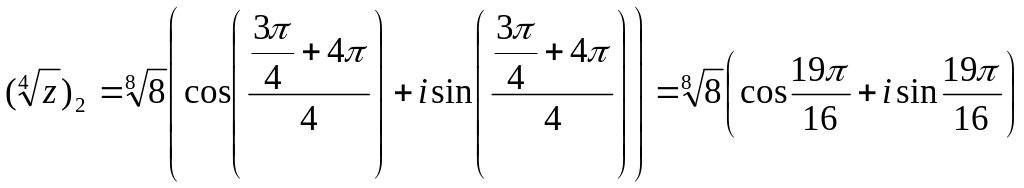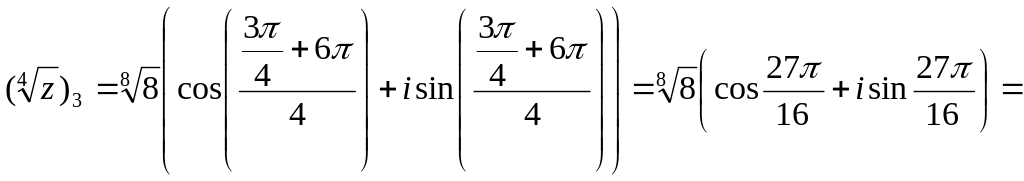
Вправи

1. Виконати дії:

1) ; 2) ; 3) ; 4) ; 5) ; 6) .

2. Знайти модуль і аргумент та представити в тригонометричній формі:

7) ; 8) ; 9) ; 10) ; 11) .

3. Обчисліть:

12) ; 13) ; 14) ; 15) .

4. Визначте геометричний зміст:

16) ; 17) ; 18) ;

19) ; 20) .

1.2. Послідовності і ряди комплексних чисел. Степеневий ряд

Означення1. Послідовністю комплексних чисел називається пронумерована нескінченна множина комплексних чисел і позначається символом

.

Означення2. Число називається границею послідовності , якщо

, ,

виконується нерівність .

Позначається цей факт символом .

Теорема 1. Необхідною і достатньою умовою збіжності послідовності , є збіжність послідовностей дійсних чисел , .

Доведення можна знайти в [1, с. 19] .

Наприклад, , , тоді , , .

Завдяки цій теореми всі властивості збіжних послідовностей дійсних чисел переносяться на випадок комплексних чисел.

Ряд , де комплексні числа, називається числовим рядом з комплексними членами і позначається , – часткова сума ряду.

Означення3. Ряд називається збіжним, якщо збігається послідовність його часткових сум . Границя називається сумою ряду .

З теореми 1 випливає, що ряд збігається тоді і тільки тоді,

коли збігаються ряди дійсних чисел , .

При цьому отримуємо: .

Ряди вигляду , , , називають степеневими рядами з центром . Множину точок, для яких степеневий ряд збігається називають областю збіжності ряду. При цьому областю збіжності степеневого ряду є круг , де , , якщо границя кінцева і відмінна від нуля. Якщо границя дорівнює , то , якщо границя дорівнює 0, то .

Детальне викладення матеріалу можна знайти в [1, 2, 3].

Приклад 1. Дослідити на збіжність ряд та обчислити його суму.

Розв’язання. Ряди і збігаються, так як вони є нескінченно спадними геометричними прогресіями.

.

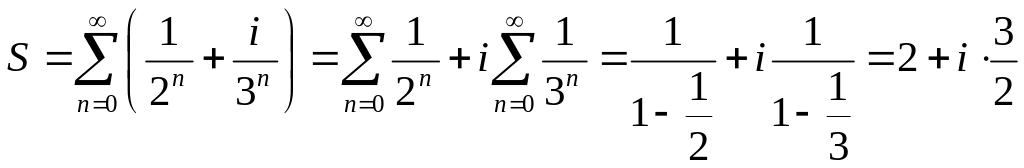Приклад 2. Знайти область збіжності ряду .

Розв’язання. , , ,

тобто , відповідно .

Область збіжності круг .

Вправи

Дослідити збіжність рядів. Знайти область збіжності.

1. 2. 3. 4. 5.

6. 7. 8. 9. 10.