
- •Змістовний модуль №1. Комплексні числа та їх геометричне представлення
- •Комплексні числа. Форми запису комплексного числа. Дії над комплексними числами
- •1.2. Послідовності і ряди комплексних чисел. Степеневий ряд
- •Змістовний модуль №2. Похідна функції комплексної змінної
- •2.1 Функції із с в с. Границя, неперервність
- •2.2. Похідна функції комплексної змінної. Умови диференційованості
- •2.3. Геометричний зміст модуля і аргументи похідної комплексної функції
- •2.4. Означення аналітичної функції. Поняття Конформного відображення
- •Змістовний модуль №3. Елементарні аналітичні функції
- •Лінійна функція
- •Дробово-лінійна функція
- •Степенева функція. Поверхня Рімана
- •Функція Жуковского
- •Показникова функція комплексної змінної
- •Тригонометричні функції
- •Логарифмічна функція. Точка розгалуження
- •Радикал. Загальна степенева функція
- •Обернені тригонометричні функції
- •Змістовний модуль №4. Інтеграл функції комплексної змінної
- •Інтеграл від функції комплексної зміної по кусочно-гладкому контуру
- •Теорема Коші
- •Невизначений інтеграл. Формула Ньютона-Лейбница
- •Змістовний модуль № 5. Інтегральна формула Коші та її наслідки
- •5.1. Формула Коші. Принцип максимума модуля
- •5.2. Цілі функції. Теорема Ліувіля. Основна теорема алгебри
- •5.3. Розкладання функції в ряд Тейлора. Оцінка коефіцієнтів степеневого ряду
- •5.4. Нулі аналітичної функції. Ізольованість нулів. Теорема єдиності
- •5.5. Аналітичне продовження. Елементарні функції як аналітичні продовження
- •Змістовний модуль № 6. Ізольовані особливі точки аналітичних функцій
- •6.1. Розкладання аналітичної функції в ряд Лорана
- •6.2. Класифікація ізольованих особливих точок. Нескінченно віддалена особлива точка. Критерій особливої точки, яка усувається
- •6.3. Критерій полюса
- •6.4. Теорема Сохоцького-Вейєрштрасса
- •6.5. Раціональні і міроморфні функції
- •Змістовний модуль № 7. Лишки та їх застосування
- •7.1. Означення ЛишкА. Обчислення лишків
- •7.2. Основна теорема теорії лишків
- •7.3. Застосування теореми лишків до обчислення визначених інтегралів
- •Контрольні роботи Контрольна робота №1 (денна форма навчання)
- •Контрольна робота №2 (денна форма навчання)
- •Контрольна робота (заочна форма навчання)
- •Зразки розв'язування задач
- •Література
Радикал. Загальна степенева функція
Означення8.
Функція
![]() –
обернена по відношенню до функції
–
обернена по відношенню до функції
![]() .
Функція
є n-значною
функцією, при цьому функції
.
Функція
є n-значною
функцією, при цьому функції
![]() називаються вітками вихідної функції.
Кожна вітка
називаються вітками вихідної функції.
Кожна вітка
![]() виконує
конформне відображення k-го
листа поверхні Римана функції
виконує
конформне відображення k-го
листа поверхні Римана функції
![]() на відповідний кут площини
(див. властивості функції
).
на відповідний кут площини
(див. властивості функції
).
![]()
При
цьому при обході точки z
по замкнутій кривій, яка містить 0
її аргумент змінюється на
,
значить і
![]() змінить
своє значення (при обході z
по кривій) з
на
,
тобто z=0
- точка розгалуження функції
(аналогічно і
z=
).
змінить
своє значення (при обході z
по кривій) з
на
,
тобто z=0
- точка розгалуження функції
(аналогічно і
z=
).
Загальна
степенева функція
![]() ,
,
![]() - визначається як
- визначається як
![]() багатозначна функція, яка має звичайні
властивості степеневої функції:
багатозначна функція, яка має звичайні
властивості степеневої функції:
1)
![]()
![]() =
=
![]() ;
;
2)
:
=
![]() ;
;
3) (
)b=
![]() ;
;
крім того, точка розгалуження z=0, z= .
Обернені тригонометричні функції
![]() - обернена
до
- обернена
до
![]() або
або
![]() .
Розв’язуючи квадратне рівняння відносно
.
Розв’язуючи квадратне рівняння відносно
![]() ,
отримаємо
,
отримаємо
![]() та
та
![]() - багатозначна функція з точками
розгалуження
- багатозначна функція з точками
розгалуження
![]() .
.
Приклад1.
Знайти
![]() .
.
Розв’язання
![]() =
=![]() .
.
Вправи
Обчислити:
1)
![]() ;
;
2)
![]()
3)
![]() ;
;
4)![]() ;
;
5)![]()
Знайти,
у що відображає вітки функції
![]()
6) ;
7) кут
![]() ;
;
8) сектор
![]() ;
;
9)![]() .
.
10)
![]() кут
кут
![]() .
.
Змістовний модуль №4. Інтеграл функції комплексної змінної
Інтеграл від функції комплексної зміної по кусочно-гладкому контуру
Нехай
С
– крива на площині z,
а функція
визначена вздовж кривої С.
Розіб’ємо криву С
з довільними точками
![]() та виберемо на дузі
та виберемо на дузі
![]() довільні точки
довільні точки
![]() .
.

Сума
![]() – інтегральна сума для даного розбиття
та вибраних точок, позначимо
– максимальну довжину дуг
,
– інтегральна сума для даного розбиття
та вибраних точок, позначимо
– максимальну довжину дуг
,![]() .
.
Означення1.
Число
![]() називається інтегралом функції
вздовж кривої С,
а функція
називається інтегрованою вздовж кривої
С,
якщо для будь-якого
називається інтегралом функції
вздовж кривої С,
а функція
називається інтегрованою вздовж кривої
С,
якщо для будь-якого
![]() існує таке
існує таке
![]() ,
що для будь-якого розбиття кривої,
параметр якого
,
що для будь-якого розбиття кривої,
параметр якого
![]() виконується нерівність
виконується нерівність
![]() незалежно від вибраних точок.
незалежно від вибраних точок.
Позначимо:
![]() .
.
Теорема1.
Нехай С
– кусково-гладка крива, а
![]() –
кусково-неперервна та обмежена, то
інтегрована уздовж С
та
–
кусково-неперервна та обмежена, то
інтегрована уздовж С
та
![]()
Доведення цього факту можна знайти [1, с.39].
Крім того, оскільки інтеграл від комплексної функції виражається через звичайні криволінійні інтеграли, то всі властивості звичайного інтегралу виконуються у випадку інтегралу від комплексної функції:
1)
![]() ;
;
2)
![]() ;
;
3)
![]()
4)
![]() ,
де
,
де![]() ,
L
– довжина кривої С
і т.д.
,
L
– довжина кривої С
і т.д.
Приклад1.
Обчислити
![]() ,
де C
– дуга
,
де C
– дуга
![]() .
.
Розв’язання.
![]() ,
,
![]()
![]() .
.
Вправи
Обчислити
![]()
по півколу
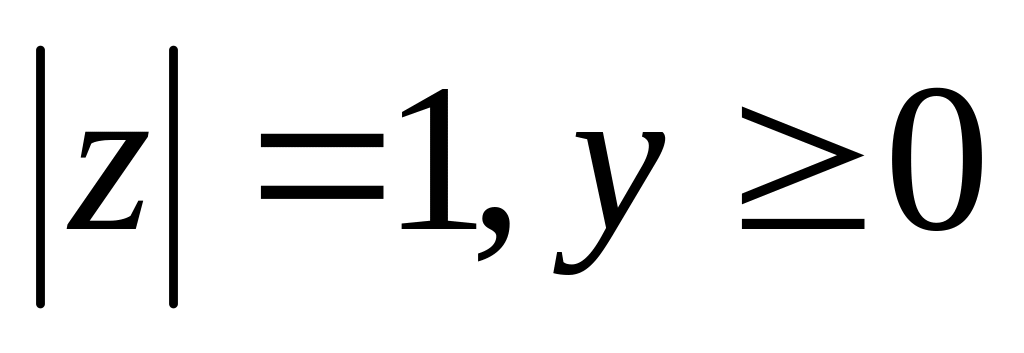 та
та
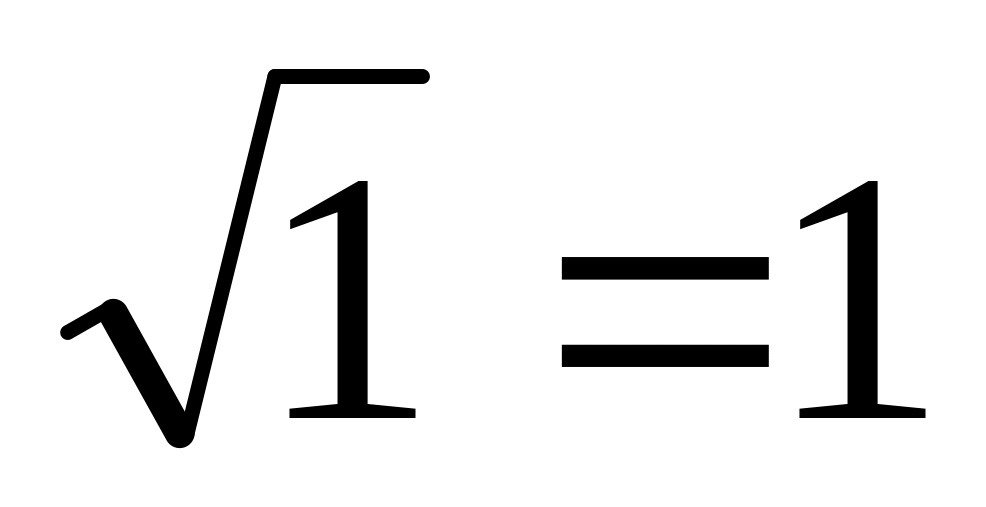 ;
;по півколу та
 ;
;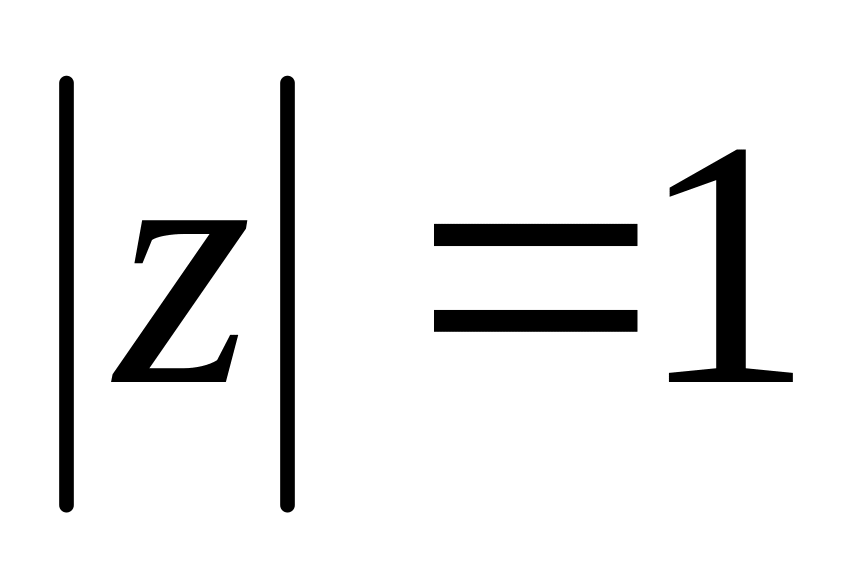 та
;
та
;та
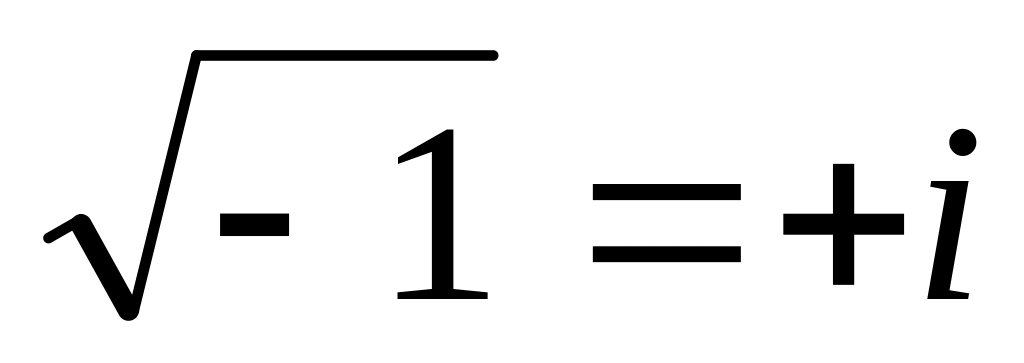 ;
; ,
С
– замкнений контур, який складається
з верхнього півкола
та відрізку
,
С
– замкнений контур, який складається
з верхнього півкола
та відрізку
 .
.
Обчислити
![]() :
:
та
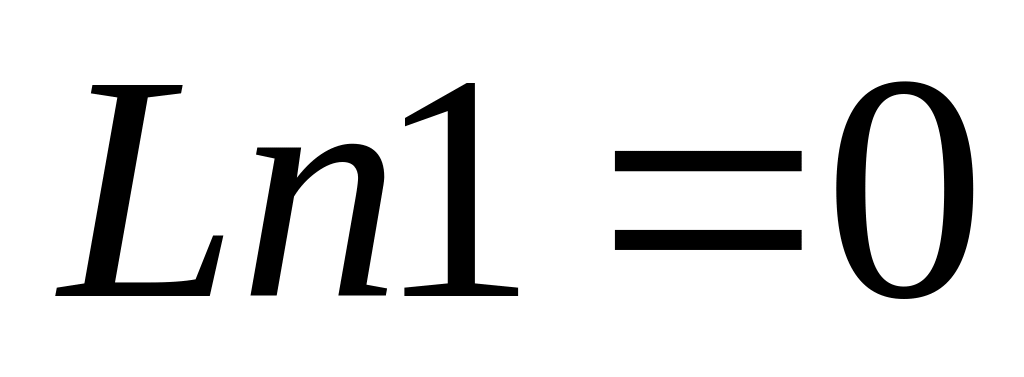 ;
;,
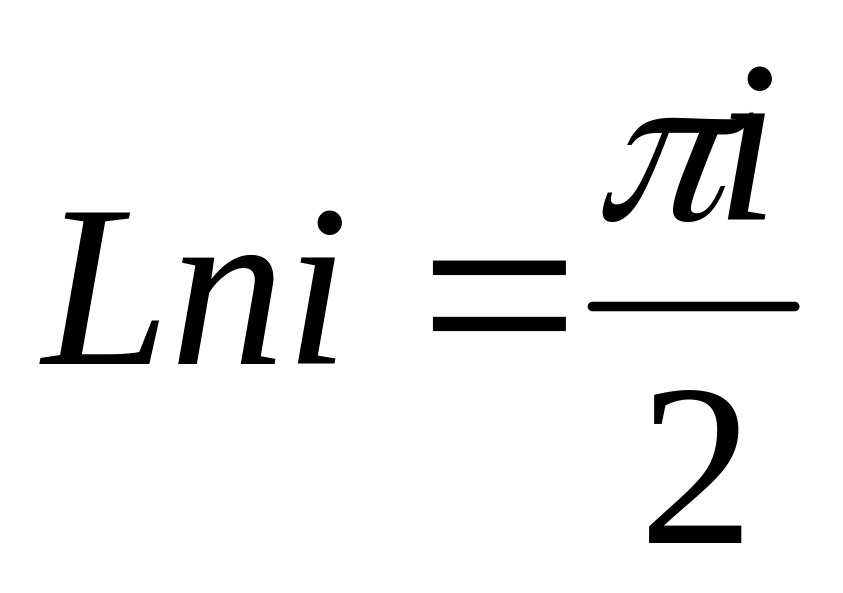 ;
;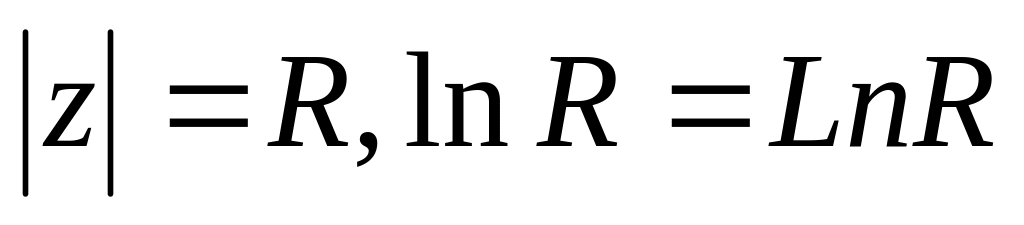 ;
;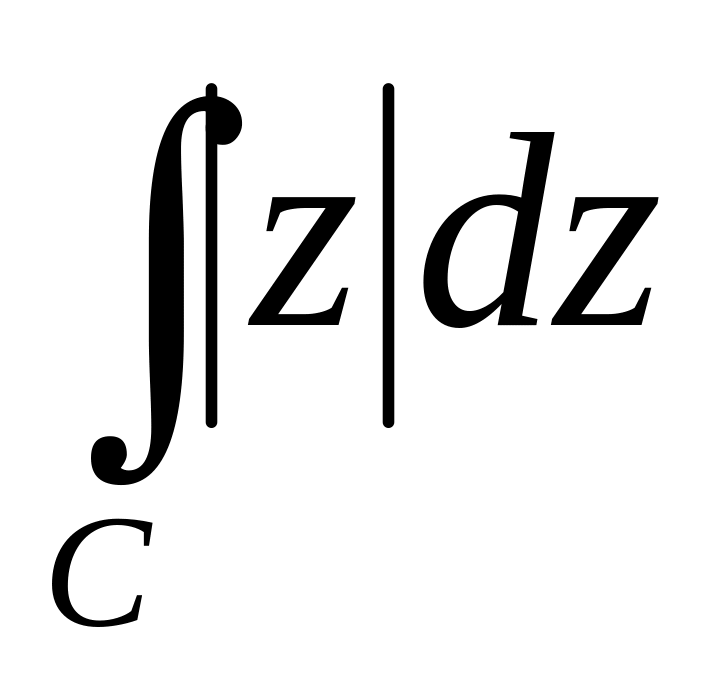 С:
радіус-вектор
С:
радіус-вектор
 ;
;
10) ![]() С:
початок шляху в точці z=1.
С:
початок шляху в точці z=1.
Теорема Коші
Теорема2 (перша теорема Коші). Нехай у однозв’язній області задана однозначна аналітична функція . Тоді інтеграл від цієї функції по будь-якому замкнутому контуру , який цілком лежить в області , дорівнює нулю, тобто
![]() .
.
Теорема3 (друга теорема Коші). Якщо функція є аналітичною функцією у однозв’язній області , обмеженої кусково-гладким контуром С, та неперервна у замкнутій області , то
![]() .
.
Наслідок1.
Нехай
є аналітичною функцією у багатозв’язній
області
,
обмеженої ззовні контуром
![]() ,
а з середини – контурами
,
а з середини – контурами
![]() та
неперервна у замкнутій області
.
Тоді
та
неперервна у замкнутій області
.
Тоді
![]() ,
,
де С
– повна границя
![]() ,
причому обхід границі С
виникає у додатковому напрямку, тобто,
область при обході зліва.
,
причому обхід границі С
виникає у додатковому напрямку, тобто,
область при обході зліва.
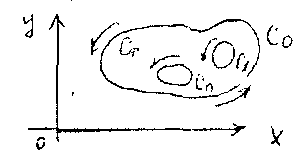
При
цьому
![]()
![]()
![]() (
(![]() обходяться у додатковому напрямку,
тобто проти часової стрілки).
обходяться у додатковому напрямку,
тобто проти часової стрілки).
Доведення: див. [1, с.41].
Наслідок2.
В умовах теореми Коші для будь-якої
кусочно-гладкої кривої, яка з’єднує
точки
та
![]() інтеграл від
не залежить від вибраного шляху.
інтеграл від
не залежить від вибраного шляху.
