3.4. Тривимірні узагальнення килима Серпінського

Застосуємо ідею узагальнення килима Серпінського, описану в першому розділі для тривимірного випадку. Отже, візьмемо куб і розіб’ємо його на 27 конгруентних кубів, які в тричі менші за початковий куб. Будемо вилучати деяку кількість кубів, а з тими кубами що залишились проробимо ту ж процедуру що й з початковим кубом і так до нескінченності. В результаті в границі будемо отримувати самоподібні об’єкти.

На рис 3.6 зображений приклад етапів побудови одного з таких обєктів.

……

Рис. 3.6. Перші етапи побудови фрактала.

Всього таких об’єктів буде (не зрозуміло), включаючи фрактальну піну, губку Менгера і об’ємний пил Кантора. Але серед них є і однакові, вони отримані поворотами початкового куба відносно своїх осей симетрії, тобто самосуміщеннями.

Для того, щоб встановити всі самосуміщення куба розглянемо спочатку лише ті самосуміщення куба ABCDA₁B₁C₁D₁ (рис. 3.7), які одну з вершин, – нехай А, – суміщають саму з собою.

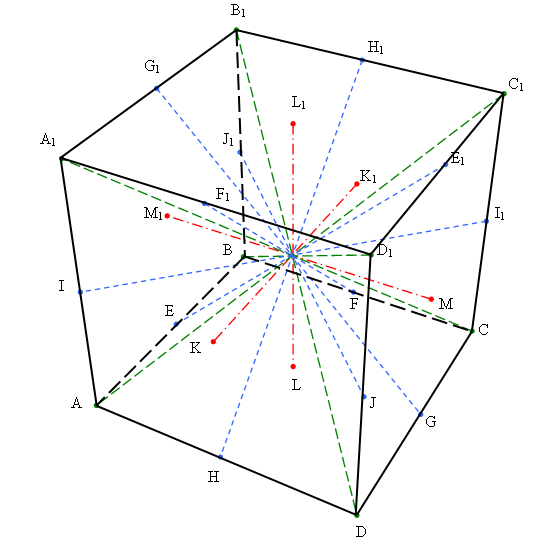
Рис. 3.7.

При кожному самосуміщенні куба вершина переходить у вершину, ребро в ребро, грань в грань; також і діагоналі куба переходять в самих себе. Якщо дане самосуміщення залишає вершину А нерухомою, то воно залишає нерухомою і діагональ АС₁ (оскільки існує лише одна діагональ куба, що виходить з вершини А). Отже, дане самосуміщення є поворот куба навколо діагоналі АС₁ на певний кут α ( ). Таких поворотів, окрім тотожного, є два: на кут 2π/3 і на кут 4π/3: , .

Отже, є всього три самосуміщення куба, що переводять вершину А в саму себе. Але вершину А належно підібраним поворотом можна перевести в кожну з восьми вершин куба; звідси, легко виводимо, що всіх самосуміщень куба є 3•8 = 24.

Постараємося визначити кожне з цих самосуміщень. Відмітимо передусім, що у куба є наступні 13 осей симетрії: чотири діагоналі, три прямі, що з’єднують попарно середини граней куба, шість прямих, що з’єднують попарно середини протилежних ребер куба (рис. 3.7).

Навколо кожної з чотирьох діагоналей є два нетотожні повороти куба, що суміщають куб з самим собою, а отже всього маємо вісім поворотів навколо діагоналей ( , , , , , , , ).

Навколо кожної з прямих, що з’єднують центри протилежних граней куба, є три нетотожні повороти. Отже, всього таких поворотів 9 ( , , , , , , , , ).

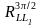Нарешті, маємо один нетотожний поворот (на кут π) навколо прямої, що сполучає середини двох протилежних ребер; загальне число цих поворотів рівне шести ( , , , , , ).

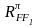Отже, маємо 8 + 9 + 6 = 23 нетотожні повороти, що суміщають куб з самим собою. Якщо приєднати до них ще тотожний поворот, одержимо 24 самосуміщення, тобто всі самосуміщення куба, які тільки є [1].

За теоремою Пойа твірна функція запасу для групи самосуміщень куба буде [15]:

Дана функція дозволяє визначити скільки існує об’єктів даної розмірності. Наприклад, треба визначити скільки існує об’єктів розмірності . Для цього треба знайти коефіцієнт біля . Отже, об’єктів розмірності існує рівно 4 (див. додаток Б).

Таким чином знайшовши суму всіх коефіцієнтів визначимо, що всього варіантів таких об'єктів 5605504, але серед них є куб і порожня множина, тобто залишається 5605502 об’єктів [5].