9.3. Понятие о производной вектора по скалярному аргументу

При рассмотрении задач кинематики и динамики мы встретимся с необходимостью вычисления производных векторов, имеющих различный физический смысл и являющихся функциями различных скалярных аргументов (времени, дуги и пр.). Поэтому в начале этого параграфа мы определим понятие производной вектора по скалярному аргументу в общем виде, не придавая конкретного физического значения вектору и аргументу.

Пусть вектор задан в какой-либо системе координат как непрерывная функция скалярного аргумента

.

П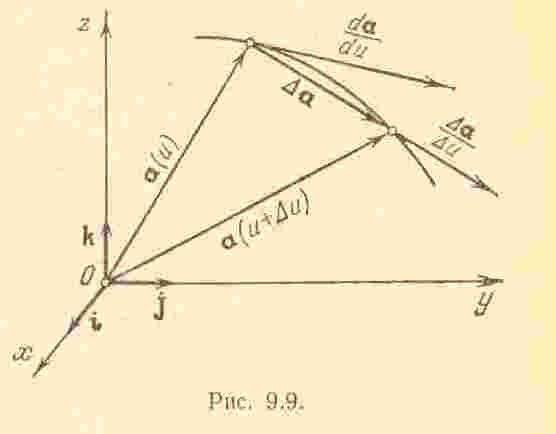 ри изменении аргумента будет меняться как модуль вектора , так и его направление. Конец вектора при изменении аргумента описывает кривую – годограф вектора . Пусть – некоторое фиксированное значение аргумента, а – его приращение. Тогда при значении аргумента вектор будет иметь другой модуль и другое направление, чем при значении аргумента, равном .

Разность

называется приращением вектора .

Предел отношения

при , если он существует, называется производной вектора по скалярному аргументу и обозначается через , т.е.

.

Заметим, что вектор всегда направлен по секущей годографа вектора , а значит, и вектор направлен также по секущей. При секущая займет предельное положение, совпадающее с касательной к годографу вектора . Следовательно, производная вектора по скалярному аргументу всегда направлена по касательной к годографу этого вектора.

Приведем без доказательства свойства производной вектора по скалярному аргументу:

1. Производная постоянного по величине и направлению вектора равна

нулю.

2. Производная суммы векторов равна сумме производных, т.е.

.

3. Производные скалярного и векторного произведений векторов

соответственно определяются выражениями:

,

.

Пусть вектор задан в неподвижной прямоугольной системе координат, тогда

,

где , , – проекции вектора на оси . Так как векторы постоянные, то

.

С другой стороны, вектор можно записать через его проекции следующим образом:

.

Сравнивая оба выражения, найдем проекции производной вектора на координатные оси

, , .

Эти равенства можно прочитать следующим образом: проекции производной вектора на неподвижные оси равны производным от соответствующих проекций вектора.

Модуль производной определяется из равенства

.

Если модуль вектора остается постоянным при изменении аргумента , то годографом вектора будет кривая, расположенная на сфере радиуса . Следовательно, производная , направленная по касательной к годографу вектора , будет в этом случае перпендикулярна вектору .

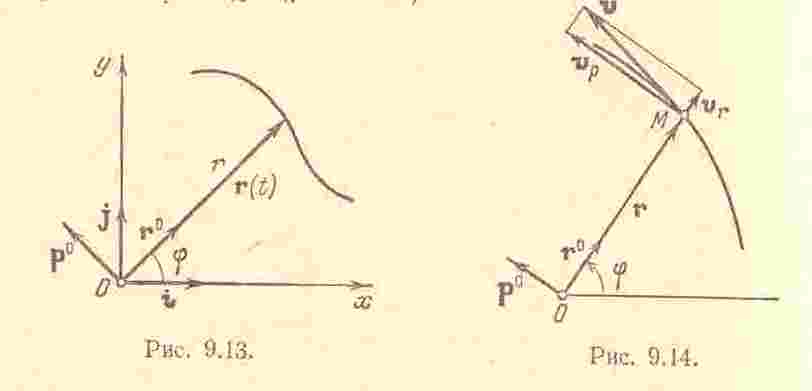
9.4. Скорость точки

Перейдем теперь к определению понятия скорости точки и методам ее нахождения.

Пусть в момент времени положение точки определяется радиусом-вектором , а в момент – радиусом-вектором . Вектор

будем называть вектором перемещения за время .

Отношение вектора к промежутку времени называется средней скоростью точки за промежуток времени

.

С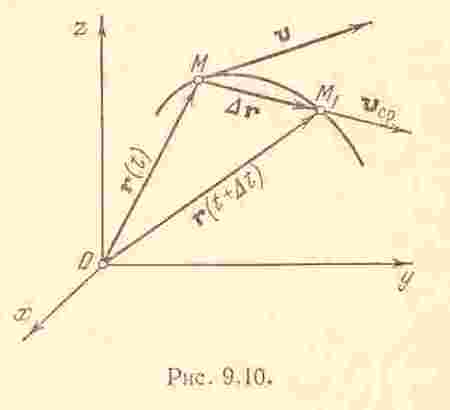 коростью в данный момент времени называется предел отношения сектора перемещения точки к промежутку времени, за который произошло это перемещение, когда этот промежуток времени стремится к нулю, т.е.

.

Размерность скорости будет

.

Единицами измерения могут быть , , .

Из этого определения видно, что скорость точки равна произведению радиуса-вектора точки по времени. На рис. показаны средняя скорость и скорость точки . Как следует из общей теории, скорость точки – это вектор, направленный по касательной к траектории в сторону движения точки.

Скорость точки при координатном способе задания движения. Пусть движение точки задано в декартовой системе координат, принятой за неподвижную, т.е. пусть заданы координаты точки как функции времени

, , .

Согласно выражению (9.8) имеем

.

Так как единичные векторы выбранной системы координат постоянны, то на основании формулы (9.11) получаем

.

На рис. показано разложение скорости на составляющие по осям координатной системы .

Таким образом, проекции скорости , , на координатные оси будут

, , ,

т.е. проекция скорости точки на координатную ось равна первой производной по времени от соответствующей этой оси координаты.

Т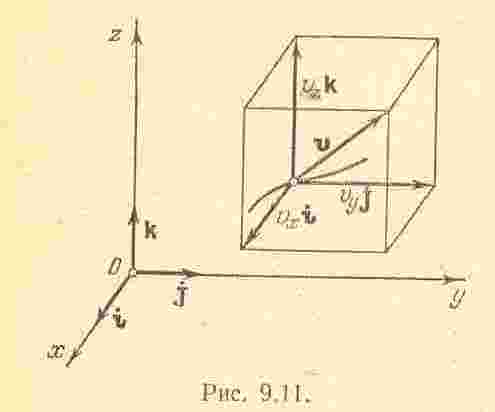 ак как производную по времени мы условились обозначать точкой сверху, то полученные формулы можно переписать в виде

, , . (9.12)

Модуль скорости определяется формулой

, (9.13) а направление скорости – направляющими косинусами

(9.14)

Если модуль скорости не изменяется с течением времени, то движение называется равномерным.

Задача 9.4. Движение точки задано уравнениями

, , .

Найти скорость точки.

Решение. В соответствии с выражениями (9.12) получим проекции скорости

, , .

Модуль скорости определяется формулой (9.13)

.

Направление скорости найдем, используя формулы (9.14)

Из этих соотношений видно, что точка движется равномерно , но направление скорости изменяется с течением времени.

Исследуем траекторию точки. Из первых двух уравнений движения найдем

.

Это – уравнение цилиндра радиуса , ось которого совпадает с осью .

О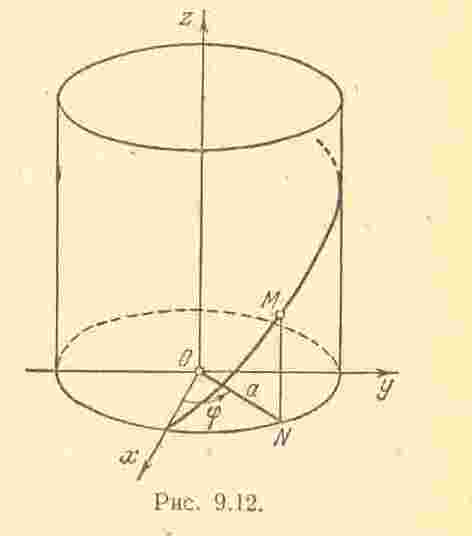 пустим теперь из точки на плоскость перпендикуляр и обозначим угол между осью и прямой через . Координаты точки будут

, .

Сравнивая эти соотношения с уравнениями движения, найдем

.

Таким образом, угол изменяется пропорционально времени. Из этого следует, что прямая равномерно вращается, а точка в это время равномерно перемещается по образующей . Следовательно, точка движется по винтовой линии. Уравнения линии в параметрической форме совпадают с уравнениями движения, а в координатной форме имеют вид

, .

Рассмотрим теперь движение, заданное в полярных координатах, т.е пусть даны как функции времени полярный радиус и угол , определяющие положение точки.

Введем в рассмотрение единичные векторы: , направленный по радиусу-вектору в сторону возрастания , и , повернутый относительно на угол в сторону возрастания угла . Единичные векторы и могут быть представлены через единичные векторы координатных осей:

,

.

В дальнейшем нам будут нужны выражения для производных по времени от единичных векторов , .

Дифференцируя по времени, получим

. (9.15) Аналогично

. (9.16)

Радиус вектор , определяющий положение точки, может быть представлен в виде . При движении точки меняются как модуль, так и направление радиуса-вектора , следовательно, и , и являются функциями времени. На основании равенства (9.11) имеем

.

Используя соотношение (9.15), будем иметь

.

Полученная формула дает разложение вектора скорости на две взаимно перпендикулярные составляющие: радиальную и поперечную .

Проекция скорости на радиальное и поперечное направления

и (9.17) называются соответственно радиальной ­­и поперечной скоростями.

Модуль скорости находится по формуле

. (9.18)

Формулу (9.18) можно получить, используя связь между декартовыми и полярными координатами,

, .

Продифференцировав эти соотношения по времени , и используя равенство (9.13), получим

.

Нахождение скорости при естественном способе задания движения. Пусть точка движется по какой-либо кривой. За промежуток времени точка переместится из положения в положение . Дуга , если движение точки происходит в сторону положительного отсчета дуги, и если, если движение происходит в противоположную сторону. На основании (9.11) имеем

.

Перепишем это равенство в виде

.

Т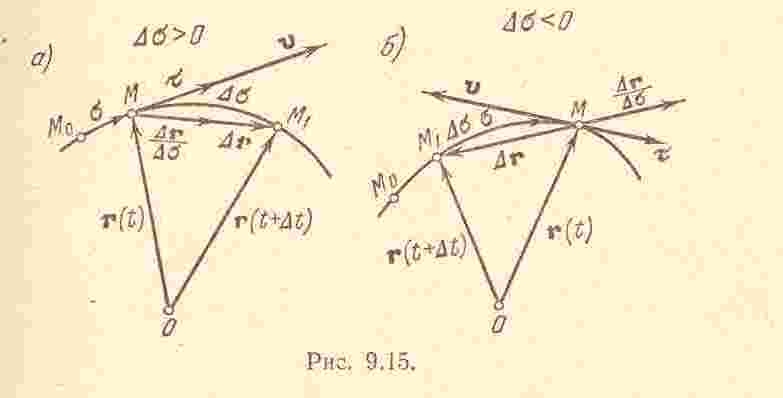 ак как предел отношения дуги к стягивающей ее хорде равен по модулю единице, а предельное положение секущей совпадает с направлением касательной к кривой в точке ,то

,

где – единичный вектор касательной к кривой, направленный в сторону положительного отсчета дуги.

Действительно, если , то вектор направлен в сторону , а при вектор направлен в сторону, противоположную . В обоих случаях этот вектор, а следовательно, и его предел , направлены в сторону возрастания дуги (на рис. положительное направление отсчета дуги выбрано вправо от начала отсчета ).

Принимая во внимание, что

,

имеем

. (9.19)

Обозначая , получим

. (9.20) Из формулы (9.20) следует, что . Очевидно, что , если движение происходит в сторону положительного отсчета дуги, и , если движение происходит в противоположную сторону.

Так как проходимый точкой путь всегда положителен, то элемент пути

и, следовательно, модуль скорости можно определить по формуле

.