9.8. Задачи

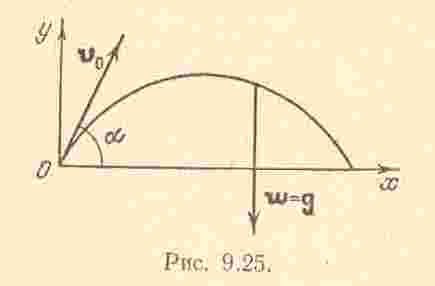
Задача 9.7. Снаряд движется в вертикальной плоскости согласно уравнениям , . Определить скорость и ускорение снаряда в начальный момент времени, высоту траектории, дальность полета, а также радиус кривизны в начальной и наивысшей точках траектории. Ось направлена горизонтально, а ось – вертикально вверх.

Решение. Траекторией снаряда, очевидно будет парабола

.

Определим сначала скорость движения снаряда. Имеем

.

Следовательно,

.

В момент времени величина скорости . Направление скорости определяется по формулам

При получим

т.е. скорость в начальный момент образует с осью угол .

Проекции ускорения на координатные оси будут

, ,

следовательно, модуль ускорения равен

,

и оно направлено по вертикали вниз (ускорение свободного падения). Под высотой траектории понимается максимальное значение ординаты . Очевидно, что принимает максимальное значение при , т.е. когда

.

Находя отсюда и подставляя его в уравнение для , получим

.

Дальность полета определяется из условия . Из уравнения

найдем

, .

Момент соответствует начальному положению снаряда. Подставляя в уравнение для , найдем дальность полета

.

Максимальная дальность полета будет при и равна

.

Найдем теперь радиус кривизны траектории в начальной и наивысшей ее точках. Из формулы имеем

.

Таким образом, задача нахождения радиуса кривизны траектории сводится к нахождению скорости и проекции ускорения на нормаль.

Согласно (9.33) имеем

.

Так как движение точки происходит все время в сторону возрастания дуги, , и, следовательно,

При , а так как , то и, следовательно, радиус кривизны траектории в начальной точке равен

.

Для момента времени , соответствующего наивысшей точке траектории, , поэтому .

Скорость точки в этот момент равна и радиус кривизны в наивысшей точке траектории будет

.

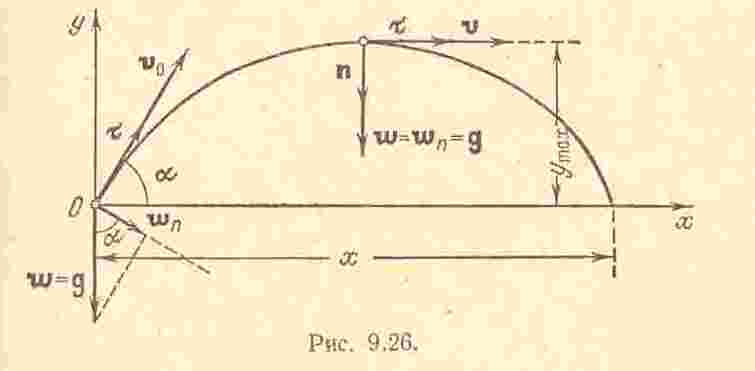
Отметим, что в данной задаче проекцию ускорения на нормаль в начальной и наивысшей точках траектории можно легко найти и простым проектированием.

З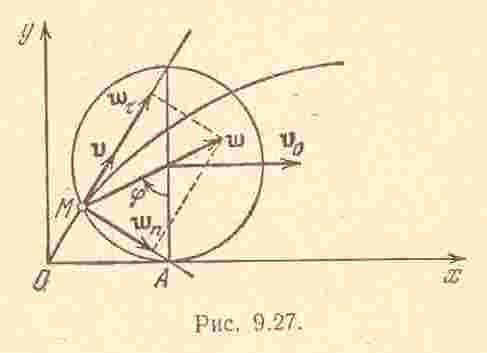 адача 9.8. Колесо радиуса катится без скольжения по горизонтальному рельсу. Скорость центра колеса постоянна и равна . Найти уравнения движения точки , лежащей на ободе колеса, ее траекторию, скорость, ускорение и радиус кривизны траектории как функцию времени.

Решение. По условию, колесо катится без скольжения, следовательно, дуга равна отрезку при предположении, что в начальный момент времени точка находилась в точке .

Так как дуга , а , то и , где .

Координаты точки будут:

,

.

Эти уравнения можно рассматривать как параметрические уравнения траектории, которая представляет собой циклоиду.

Проекции скорости точки на оси и равны

,

.

Модуль скорости равен

.

Заметим, что угол изменяется от нуля до и поэтому .

Направляющие косинусы вектора скорости будут

Отсюда следует, что вектор скорости все время проходит через верхнюю точку колеса.

Проекции ускорения на оси и равны

,

и, следовательно,

,

а так как

то вектор ускорения точки всегда проходит через центр колеса.

Радиус кривизны траектории найдем из выражения

.

Так как и при , то

.

Следовательно,

,

где – длина отрезка от рассматриваемой точки колеса до его нижней точки.

З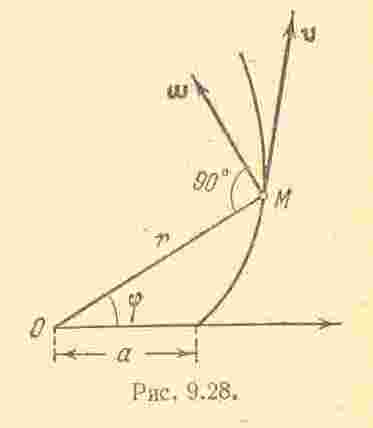 адача 9.9. Движение точки задано в полярных координатах уравнениями и , где и – постоянные величины.

Найти уравнение траектории, скорость, ускорение и радиус кривизны траектории точки как функции ее радиуса .

Решение. Исключая из уравнений и время , получим уравнение траектории

.

Это – уравнение логарифмической спирали.

Согласно формуле (9.17) радиальная и поперечная составляющие скорости соответственно будут

,

.

Следовательно, скорость точки равна

.

Согласно формулам (9.26) будем иметь

,

,

т.е. ускорение точки

.

Определим теперь радиус кривизны траектории. На основании (9.32) получим

.

Скорость нами уже определена. Найдем . Согласно (9.33)

;

имеем

.

Таким образом,

.

Итак, радиус кривизны траектории

.

Задача 9.10. Радар , установленный на берегу, непрерывно следит за движением судна , определяя в каждый момент расстояние и угол между меридианом и направлением радара на судно, а также скорости изменения этих величин. Пренебрегая кривизной земной поверхности, определить модуль скорости судна относительно Земли, его курс (угол между меридианом и скоростью ) и расстояние от радара до направления скорости .

Для решения задачи построим прямоугольную систему координат , направив ось по касательной к меридиану на север, а ось по касательной к параллели на запад. Величины , , и , которые непрерывно измеряет радар, суть полярные координаты судна и их скорости. Поэтому модуль скорости будет (9.18):

.

Для определения курса (угла ) разложим вектор скорости судна на радиальную и поперечную составляющие. Имеем (см. рис.):

(углы и – соответственные при параллельных прямых и , а – внешний для треугольника ).

Из треугольника найдем

,

или, учитывая значения проекций поперечной и радиальной составляющих скорости ,

. (9.34)

Отсюда

. (9.35)

Из треугольника найдем параметр :

. (9.36)

С помощью компьютера скорость судна , его курс и параметр непрерывно определяются по формулам (9.18), (9.35) и (9.36) или им эквивалентным.

Если судно идет постоянным курсом , т.е. движется по прямой линии , то равенство (9.36) определяет уравнение траектории судна в полярных координатах. Покажем, что при это уравнение может быть получено из равенства (9.34).

Д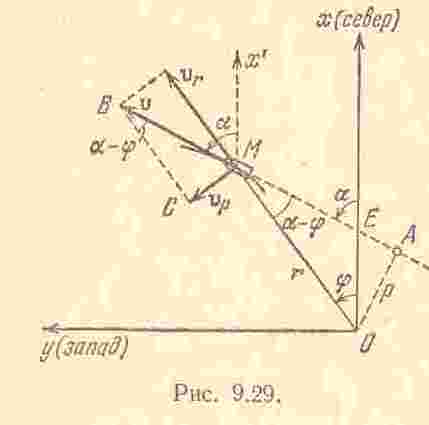 ействительно, умножая числитель и знаменатель

правой части равенства (9.34) на , получим

,

или

.

Интегрируя обе части этого равенства и учитывая, что по предположению , получим

, (9.37) где – произвольная постоянная интегрирования. При расстояние от радара до судна будет равно , т.е. . Подставляя эти значения в (9.37), найдем

или

.

Внося это значение для в равенство (9.37), получаем

,

откуда следует равенство (9.36)

.

Задача 9.11. Угол между неподвижной осью и кривошипом изменяется по закону , где – постоянное положительное число. С кривошипом в точке шарнирно соединен стержень , проходящий постоянно через качающуюся муфту . Найти уравнения движения точки стержня , отстоящей от точки на расстоянии , ее траекторию, скорость и ускорение, если .

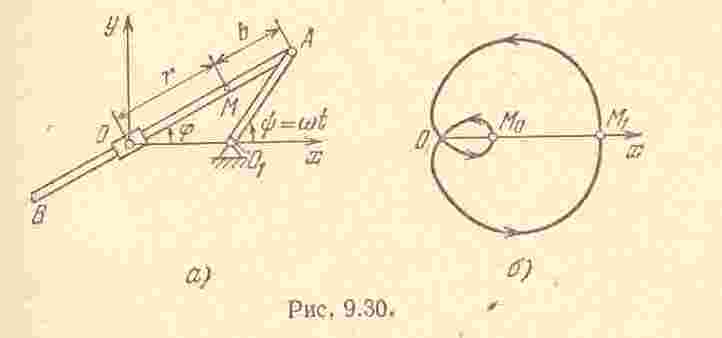
Решение. Положение точки проще всего определяется полярными координатами: радиусом и полярным углом . Так как треугольник равнобедренный, то , а сторона . Из рис. имеем ; следовательно, уравнения движения точки будут:

,

.

Исключая отсюда время , найдем уравнение движения точки в полярных координатах:

.

(Для сравнения самостоятельно найти уравнения движения и траекторию в декартовых координатах).

На рис. показана траектория точки , построенная по точкам для случая (при получается обычная кардиоида). Точка – начальная точка траектории, соответствующая моменту времени или . Направление движения точки показано стрелками. Отметим, что точка попадет в свое начальное положение не через один оборот кривошипа , а через два оборота, когда угол изменится на , а угол на радиана (это произойдет в момент времени ).

Найдем проекции скорости точки на радиальное и поперечное направления. Имеем

,

.

Теперь найдем модуль скорости точки :

,

или, подставляя найденные значения для и и произведя очевидные преобразования, получим

.

Для ускорения будем иметь:

,

.

Модуль ускорения

.

В начальной точке при :

,

.

Через один оборот кривошипа , точка попадет в положение и ее скорость и ускорение будут соответственно равны

,

.