9.2. Способы задания движения

Прежде всего определим, что значит задать движение.

Движение точки по отношению к избранной системе отсчета считается заданным, если известен способ, при помощи которого можно определить положение точки в любой момент времени. Следовательно, задать движение точки это значит указать способ, позволяющий в любой момент времени определить ее положение по отношению к выбранной системе отсчета.

Векторный способ. Положение точки в пространстве будет вполне определено, если ее радиус-вектор , проводимый из какого-либо заданного центра, известен как функция времени, т.е. . Следует, однако, иметь в виду, что задать вектор как функцию времени значит уметь находить его модуль и направление в любой момент времени. Это можно сделать, если избрана какая-либо определенная система, т.е. задание радиуса-вектора как функции времени обязательно предполагает наличие системы координат, но в то же время не конкретизирует ее. Считая, что радиус-вектор задан, мы тем самым должны предполагать, что умеем определять его модуль и направление в избранной нами системе координат.

То обстоятельство, что введением радиуса-вектора, определяющего положение точки, мы не связываем себя с конкретной системой координат, позволяет широко использовать задание радиуса-вектора как функции времени для получения основных кинематических характеристик движения. Для решения же конкретных задач обычно переходят от векторного способа к координатному и естественному способам задания движения.

Введем еще одно полезное для дальнейшего понятие о годографе вектора, рассматриваемого как функция скалярного аргумента (например, времени).

Годографом какого-либо вектора называют кривую, которую вычерчивает конец этого вектора (предполагается, что начало вектора находится все время в одной и той же точке) при изменении его аргумента.

Следовательно, годографом радиуса-вектора, определяющего положение точки буде траектория точки.

Перейдем теперь к рассмотрению координатного и естественного способов задания движения.

Координатный способ. Положение точки по отношению к какой-либо системе координат полностью определяется координатами точки. Поэтому задание координат точки в виде известных функций времени дает возможность определить ее положение в любой момент времени. Способ задания движения, заключающийся в задании координат точки как известных функций времени, называется координатным способом задания движения и требует выбора конкретной системы координат. Этот выбор определяется содержанием решаемой задачи; предпочтительнее та система координат, использование которой наиболее целесообразно для данной задачи.

При рассмотрении движения в прямоугольной декартовой системе координат указанный способ заключается в задании координат , , точки как известных функций времени, т.е.

, , . (9.1)

Во многих случаях бывает предпочтительнее использовать цилиндрические или сферические координаты.

В цилиндрических координатах положение точки определяется радиусом , углом (азимут) и аппликатой .

Следовательно, движение будет задано, если , и будут известными функциями времени

, , . (9.2)

В сферических координатах положение точки определяется полярным радиусом , углом и углом (полюсный угол). Следовательно, движение будет задано, если

, , (9.3) – известные функции времени.

Формулы, связывающие цилиндрические и сферические координаты с декартовыми, соответственно будут

, , ;

, , ,

При движении точки в плоскости иногда целесообразно использовать полярные координаты. В этом случае нужно задать в виде функций времени координаты и :

, .

Связь этих координат с декартовыми дается формулами

, .

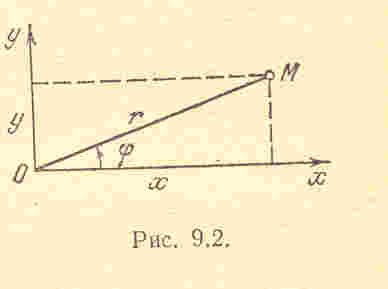Уравнения (9.1) движения точки представляют одновременно траектории в параметрической форме, где роль параметра играет время . Если требуется определить уравнение траектории в координатной форме, то требуется исключить каким-либо образом из этих уравнений время .

Задача 9.1. Движение точки в плоскости задано при помощи уравнений

, , , , (9.4) и движение начинается в момент времени . Найти уравнение траектории в координатной форме.

Решение. Из первого уравнения следует, что , поэтому уравнение траектории будет

.

Э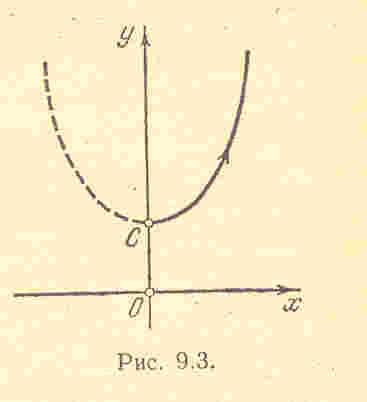 то – уравнение параболы. Однако траекторией будет не вся парабола, а только часть ее. Это следует из того обстоятельства, что от начального момента движения (когда , ) координата будет увеличиваться (время положительно и непременно возрастает). Направление движения точки по траектории определяется из уравнений (9.4) и показано на рис. стрелкой.

В рассмотренном примере исключение времени из уравнения для и подстановки в уравнение для . Такой прием не всегда удобен, поэтому исключение времени можно производить и другими способами.

Задача 9.2. Движение точки в плоскости задано уравнениями

, . (9.5) Найти уравнение траектории в координатной форме.

Решение. Уравнения и

следует возвести в квадрат и сложить. Тогда получим уравнение траектории

.

Она представляет собой эллипс. Из уравнений (9.5) следует, что движение начнется в точке А с координатами , и будет происходить в направлении, указанном стрелкой (предполагается, что движение начинается в момент времени ).

Естественный способ. При естественном способе задания движения указывают траекторию точки и закон ее движения по этой траектории.

Пусть точка движется по отношению к выбранной системе отсчета по заданной траектории, определяемой уравнениями

(9.6)

Пусть – какая-либо точка на траектории. Выбрав направление положительного отсчета дуги по траектории,

мы определим положение точки в любой момент времени, если будем знать, как изменяется дуга со временем

. (9.7) Эта зависимость называется законом движения.

Кривая, построенная на плоскости , выражающая зависимость , называется графиком движения.

Если движение происходит в сторону возрастания дуги , то дифференциал дуги^

будет положительным, если же движение происходит в сторону убывания дуги, то дифференциал дуги будет отрицательным. Отметим, что путь , проходимый точкой, всегда будет возрастать, и всегда положителен

.

Задача 9.3. Закон движения точки по траектории имеет вид

( – в сек, – в м). Построить и исследовать график движения.

Решение. Графиком движения будет кривая, изображенная на рис. Из рассмотрения этого графика следует, что дуга увеличивается до значения при , а затем начинает уменьшаться. Ход графика движения в области отрицательных характеризует увеличение абсолютного значения дуги при движении точки от начала отсчета в сторону, противоположную положительному отсчету дуги.

На рис. показана и кривая , представляющая график функции , где – путь, пройденный точкой. До значения кривая совпадает с кривой , для показана пунктиром.

Все рассмотренные способы движения взаимосвязаны.

Пусть, например, движение задано координатным способом в виде (9.1). Очевидно, что при этом проекции радиуса-вектора на оси координат равны координатам точки и, следовательно, можно записать

, (9.8) где , и – единичные векторы осей х, у, z.

Модуль найдется по формуле

, (9.9) а направление определится направляющими косинусами

, , . (9.10)

Рассмотрим еще переход от координатного способа к естественному.

Пусть движение задано уравнениями (9.1). Исключая из этих уравнений время , получим уравнение траектории (9.6). Найдем теперь закон движения .

Дифференциал дуги может быть найден по формуле

,

г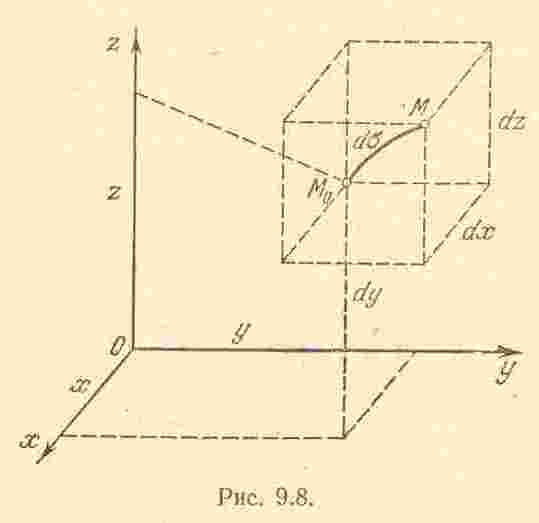 де , , – дифференциалы координат точки

, , .

Формулу для можно переписать в виде

.

Интегрируя это выражение в промежутке от (начало движения) до какого-либо момента времени , получим закон движения

.

Знак "плюс" или "минус" перед интегралом ставится в зависимости от выбора направления положительного отсчета дуги; если движение точки начинается в сторону выбранного положительного отсчета дуги, то следует брать знак "плюс", в противном случае – знак "минус".