
- •Глава IX
- •9.1. Введение
- •9.2. Способы задания движения
- •9.3. Понятие о производной вектора по скалярному аргументу
- •9.4. Скорость точки
- •9.5. Задачи
- •9.6. Ускорение точки
- •9.7. Частные случаи движения точки
- •9.8. Задачи
- •9.9. Криволинейные координаты
- •Глава X
- •10.1. Задание движения твердого тела.
- •10.2. Простейшие движения твердого тела.
- •Глава XI
- •11.1. Задание движения
- •11.2. Скорости точек при плоском движении
- •11.4. Мгновенный центр скоростей. Центроиды
- •11.5. Ускорения точек при плоском движении.
- •11.7. Задачи
- •Глава XII
- •§ 12.1. Задание движения. Углы Эйлера
- •§ 12.2. Распределение скоростей точек твердого тела, имеющего
- •Глава XIII
- •13.1. Основные определения. Абсолютная
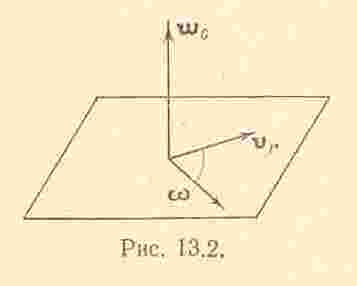
- •13.2. Теорема о сложении скоростей
- •13.3. Теорема о сложении ускорений (теорема Кориолиса)
- •Глава XIV
- •14.1. Постановка задачи
- •§ 14.2. Сложение поступательных движений
- •§ 14.3. Сложение вращений вокруг пересекающихся осей. Кинематические уравнения Эйлера
- •§ 14.4. Пара вращений
- •§ 14.5. Сложение вращений вокруг параллельных осей
- •§ 14.6. Задачи
- •§ 14.7. Сложение поступательных и вращательных движений
- •§ 14.8. Общий случай сложения движений твердого тела
13.3. Теорема о сложении ускорений (теорема Кориолиса)
Для того, чтобы найти абсолютное ускорение точки, т.е. ее ускорение по отношению к абсолютной системе координат, продифференцируем по времени формулу (13.10))
![]() .
(13.13) Абсолютную
производную вектора относительной
скорости найдем по формуле (13.5):
.
(13.13) Абсолютную
производную вектора относительной
скорости найдем по формуле (13.5):
![]() .
(13.14) В этом соотношении
.
(13.14) В этом соотношении
![]() есть относительная производная вектора
по времени и, следовательно, представляет
собой относительное ускорение
есть относительная производная вектора
по времени и, следовательно, представляет
собой относительное ускорение
![]() ,
т.е. ускорение точки по отношению к
подвижной системе координат
,
т.е. ускорение точки по отношению к
подвижной системе координат
![]() .
(13.15) Используя равенства (13.8), (13.9),
(13.14) и (13.15), преобразуем формулу (13.13) к
виду
.
(13.15) Используя равенства (13.8), (13.9),
(13.14) и (13.15), преобразуем формулу (13.13) к
виду
![]() (13.16)
где
(13.16)
где
![]() – ускорение начала подвижной системы
координат, а
– ускорение начала подвижной системы
координат, а
![]() – ее угловое ускорение.
– ее угловое ускорение.
Для того чтобы
найти переносное ускорение
![]() (ускорение той точки подвижной системы
координат, с которой в данный момент
совпадает движущаяся точка), закрепим
точку в подвижной системе координат,
т.е. положим
(ускорение той точки подвижной системы
координат, с которой в данный момент
совпадает движущаяся точка), закрепим
точку в подвижной системе координат,
т.е. положим
![]() ,
,
![]() .
.
В этом случае согласно формуле (13.16) будем иметь
![]() ,
(13.17) т.е. переносное ускорение представляет
собой ускорение точки свободного
твердого тела, с которым жестко связана
подвижная система координат. Таким
образом, имеем
,
(13.17) т.е. переносное ускорение представляет
собой ускорение точки свободного
твердого тела, с которым жестко связана
подвижная система координат. Таким
образом, имеем
![]() .
(13.18)
.
(13.18)
Ускорение,
определяемое членом
![]() ,
называют поворотным
или кориолисовым
ускорением
и обозначается
,
называют поворотным
или кориолисовым
ускорением
и обозначается
![]() ,
т.е.
,
т.е.
![]() .
(13.19) Итак, имеем
.
(13.19) Итак, имеем
![]()
 .
(13.20) Эта формула выражает
содержание теоремы Кориолиса: абсолютное
ускорение точки равно сумме переносного,
относительного и кориолисова ускорений.
.
(13.20) Эта формула выражает
содержание теоремы Кориолиса: абсолютное
ускорение точки равно сумме переносного,
относительного и кориолисова ускорений.
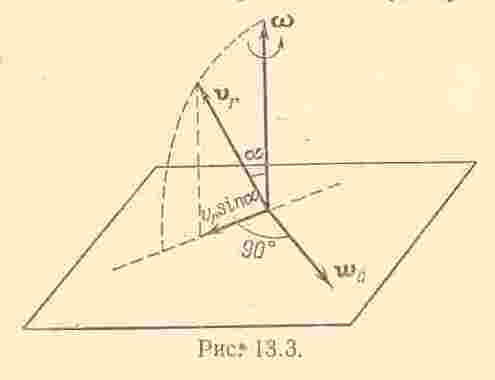
При использовании формулы (13.20) полезно иметь в виду, что переносное ускорение следует определять по правилам нахождения ускорения точек твердого тела. При нахождении относительного ускорения подвижную систему следует считать неподвижной и использовать правила, изложенные в главе 9.Остановимся несколько подробнее на кориолисовом ускорении
.
Модуль этого ускорения, очевидно, равен
![]()
 .
(13.21) Направление этого ускорения
определяется направлением векторного
произведения векторов
и
.
(13.21) Направление этого ускорения
определяется направлением векторного
произведения векторов
и
![]() ,
т.е. кориолисово ускорение будет
направлено перпендикулярно плоскости,
проходящей через векторы
и
в ту сторону, откуда кратчайший переход
от
к
виден происходящим против хода часовой
стрелки. Если векторы
и
не лежат в одной плоскости, удобно бывает
мысленно перенести вектор
параллельно самому себе в начало вектора
скорости
и применить указанное выше правило.
,
т.е. кориолисово ускорение будет
направлено перпендикулярно плоскости,
проходящей через векторы
и
в ту сторону, откуда кратчайший переход
от
к
виден происходящим против хода часовой
стрелки. Если векторы
и
не лежат в одной плоскости, удобно бывает
мысленно перенести вектор
параллельно самому себе в начало вектора
скорости
и применить указанное выше правило.
Иногда нахождение
кориолисова ускорения облегчается
применением правила Н.Е. Жуковского:
проекция
относительной скорости
на плоскость, перпендикулярную угловой
скорости
подвижной системы координат, равную
![]() ,
следует умножить на
,
следует умножить на
![]() и повернуть на угол
и повернуть на угол
![]() вокруг
в направлении вращения. Вектор, равный
по модулю
вокруг
в направлении вращения. Вектор, равный
по модулю
![]() и имеющий найденное направление, и будет
кориолисовым ускорением.
и имеющий найденное направление, и будет
кориолисовым ускорением.
На основании формулы (13.21) можно указать, что кориолисово ускорение равно нулю в следующих случаях:
 – подвижная
система координат перемещается
поступательно;
– подвижная
система координат перемещается
поступательно;угловая скорость подвижной системы параллельна относительной
скорости
![]() ;
;
в момент времени, когда относительная скорость точки равна нулю.
З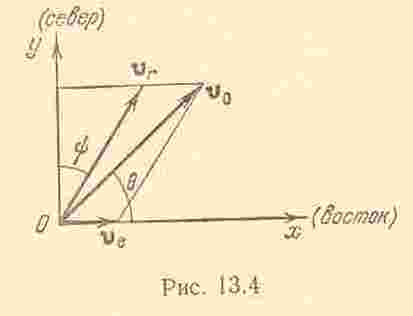 адача
13.1. Круговой спутник пролетает над
экватором. Его скорость
адача
13.1. Круговой спутник пролетает над
экватором. Его скорость
![]() .
Плоскость орбиты наклонена к плоскости
экватора под углом
.
Определить скорость движения спутника,
видимую с Земли на экваторе, ти видимое
направление движения полярного спутника
.
Плоскость орбиты наклонена к плоскости
экватора под углом
.
Определить скорость движения спутника,
видимую с Земли на экваторе, ти видимое
направление движения полярного спутника
![]() .
Радиус Земли
.
Радиус Земли
![]() .
.
Решение. Скорость движения по орбите
является абсолютной скоростью в системе
координат, движущейся поступательно с
началом в центре Земли. Земля в этой
системе координат вращается с угловой
скоростью
![]() .
.
Отложим от оси
,
касательной к экватору вектор
![]() .
Он составляет с направлением на восток
угол
.
.
Он составляет с направлением на восток
угол
.
Переносная скорость точки на экваторе равна скорости точки, участвующей во вращательном движении Земли. Следовательно, переносная скорость направлена по касательной к экватору на восток и равна по модулю
![]() .
.
Зная абсолютную и переносную скорости точки, можно определить и относительную скорость. Для этого разложим вектор на две составляющие, одна из которых равна . Определим проекции относительной скорости на оси и :
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Таким образом, угол , составленный относительной скоростью с меридианом, определится из соотношения
![]() ,
,
а модуль относительной скорости – из равенства
![]() .
.
Для полярного спутника
![]() и поэтому
и поэтому
![]() .
.
Соответствующий угол
![]() .
Знак минус указывает на то, что при
направлении абсолютного движения на
север видимое с Земли направление
скорости отклонено на северо-запад.
.
Знак минус указывает на то, что при
направлении абсолютного движения на
север видимое с Земли направление
скорости отклонено на северо-запад.
Модуль относительной скорости для полярного спутника мало отличается от модуля абсолютной скорости
![]() .
.
Задача 13.4.

Диск вращается с постоянной угловой
скоростью
![]() вокруг оси, перпендикулярной плоскости
диска и проходящей через его центр. По
прямолинейному пазу
движется
ползун
по закону
вокруг оси, перпендикулярной плоскости
диска и проходящей через его центр. По
прямолинейному пазу
движется
ползун
по закону
![]() ,
расстояние от центра диска до паза
,
расстояние от центра диска до паза
![]() ,
,
![]() .
Определить скорость и ускорение ползуна
в момент, когда он достигает середины
паза
.
Определить скорость и ускорение ползуна
в момент, когда он достигает середины
паза
![]() .
.
Решение. Абсолютная скорость ползуна
определяется по формуле
![]() .
.
В рассматриваемой задаче подвижная система координат, относительно которой происходит движение ползуна , жестко связывается с диском. Следовательно, переносной скоростью ползуна, когда он совпадает с точкой диска, будет скорость точки диска, т.е.
![]() .
.
Вектор
направлен перпендикулярно
![]() .
.
Относительное движение точки является прямолинейным. Относительная скорость равна
![]() .
.
Векторы и направлены в одну сторону, следовательно, абсолютная скорость ползуна равна
![]() .
.
Так как, то момент
![]() прохождения ползуна через точку
определится из соотношения
прохождения ползуна через точку
определится из соотношения
![]() ,
откуда
,
откуда
![]() и, следовательно, при
имеем
и, следовательно, при
имеем
![]() .
.
Абсолютное ускорение ползуна определяется формулой
.
Диск вращается с постоянной угловой
скоростью, поэтому ускорение точки
диска (в которой в момент времени
![]() находится ползун) равно
находится ползун) равно
![]() .
.
Вектор направлен к центру диска. Относительное ускорение, как ускорение точки в прямолинейном движении, будет
![]() .
.
Вектор
![]() направлен вдоль прямой
.
Так как вектор угловой скорости
и вектор
взаимно перпендикулярны, то кориолисово
ускорение будет равно
направлен вдоль прямой
.
Так как вектор угловой скорости
и вектор
взаимно перпендикулярны, то кориолисово
ускорение будет равно
![]()
и при
![]()
![]() .
.
Направление вектора
![]() указано на рис. 13.7.
указано на рис. 13.7.
Абсолютное ускорение ползуна
в момент
![]() равно
равно
![]() .
.
