13. Закон сохранения импульса и его связь с однородностью пространства.

Импульсы замкнутой системы остаются неизменными, т.е. не изменяются с течением времени. Замкнутой называется система на которую не действует влияние силы или они скомпенсированы. Другой закон сохранения возникает в связи с однородностью пространства. В силу этой однородности механические свойства замкнутой системы не меняются при любом параллельном переносе системы как целого в пространстве. В соответствии с этим рассмотрим бесконечно малый перенос на отрезок ε и потребуем, чтобы функция Лагранжа осталась неизменной.

13. Абсолютно неупругий удар.

Удар называется не упругим если тела после удара не восстанавливают свою форму и размеры. При этом импульс сохраняется, а механическая энергия – нет. В физике ударом называют такое взаимодействие тел, при котором их скорости изменяются за очень короткий промежуток времени.

После взаимодействия тела движутся либо как одно целое, либо останавливается, т.к. энергия скалярная, то энергия импульса до взаимодействия равна сумме энергии тела.

13. Абсолютно упругий удар.

Удар называют упругим, если тела полностью восстанавливаются после прекращения внешнего воздействия. В физике ударом называют такое взаимодействие тел, при котором их скорости изменяются за очень короткий промежуток времени.

13. Момент импульса и закон его сохранения.

Моментом энергии твердого тела относительно неподвижной оси называется сумма произведения материальных точек на квадрат их расстояния до рассматриваемой оси.

[I]=кг

Моменту инерции характерны инертные свойства тела при вращательном движении. Моментом импульса называют векторную величину

;

Закон сохранения момента импульса.

Если моменты всех сил на точку =0,то момент импульса не меняется.

[M]=nM

i – плечо силы или кратчайшее расстояние от линии действия силы до оси вращения.

13. Связь закона сохранения момента импульса с изотропностью пространства.

Закон сохранения момента импульса (закон сохранения углового момента) — векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем. Закон сохранения момента импульса есть проявление изотропности пространства.

13. Кинетическая энергия вращающегося тела. Расчет момента инерции полого цилиндра.

Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:

Если тело вращается вокруг неподвижной оси с угловой скоростью , то линейная скорость i-ой точки равна , где , - расстояние от этой точки до оси вращения. Следовательно.

где - момент инерции тела относительно оси вращения.

В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости центра инерции тела, и вращения с угловой скоростью вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду

где - момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.

Расчет момента инерции полого цилиндра.

Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R₁, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит

Момент инерции толстого кольца найдём как интеграл

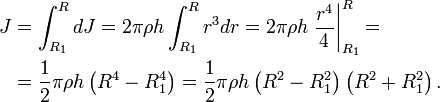
Поскольку объём и масса кольца равны

получаем окончательную формулу для момента инерции кольца