36. Поток вектора через бесконечно малую поверхность.

Потоком вектора а через бесконечно малую поверхность dS называется величина

где а — значение вектора на площадке dS, а аn — слагающая его по направлению n. Поверхность dS выбрана нами бесконечно малой именно для того, чтобы вектор а имел на этой поверхности одно определенное значение.

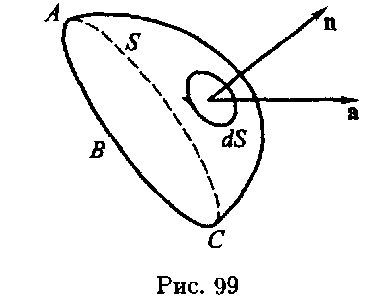
Чтобы определить поток вектора через поверхность конечных размеров, нужно разбить ее на бесконечно малые поверхности dS так, чтобы не только вектор а оставался постоянным на каждой поверхности, но чтобы и самые площадки могли считаться плоскими (рис. 99). Одну из сторон поверхности S назовем внутренней, а другую — внешней и выберем соответственным образом направление внешних нормалей к каждому из элементов dS

36. Циркуляция вектора по бесконечно малому контуру.

Проведем в векторном поле замкнутую кривую и примем для нее определенное направление обхода. Затем разобьем ее на малые дуги. Хорды, стягивающие эти элементы кривой, имеют направления, совпадающие с направлением обхода.Обозначим их   . В произвольной точке i –того участка кривой возьмем вектор поля     и составим сумму

            (2.37)

После этого устремим    к нулю. Если при этом предел суммы (2.37) существует и не зависит от способа разбиения кривой и выбора точек определения векторов  , то мы приходим к криволинейному интегралу

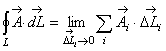         (2.38)

Криволинейный интеграл (2.38) называется циркуляцией векторного поля    по замкнутому контуруL.Если, например,    - это силовое поле, то физический смысл циркуляции состоит в том, что она выражает работу поля по пути L. Будем стягивать контур, по которому вычисляется циркуляция, к точке. Это позволит определить новую локальную характеристику отличную от дивергенции. Отличие заключается в частности в том, что ее значение будет в общем случае зависеть не только от точки, к которой стягивается контур, но и от его ориен­тации в пространстве. Поэтому можно предположить, что инте­ресующеенас предельное значение циркуляции, которая сама по себе есть скаляр, выражается через скалярноепроизведение  некоего вектора (его предстоим нам найти) и единичного вектора нормали к плоскости контура, стягиваемого к точке.Возьмем в поле   замкнутый контур L, натянем на него произвольную поверхность S  и определим на ней направление внешней нормали. Построим на ее малом участке, который в пределе можно считать плоским, прямоугольник. Его стороны обозначим    и    , причем     . Площадь этого прямоугольника

  (2.39)

, а вектор единичной нормали

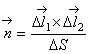           (2.40)

Вычислим циркуляцию вектора    вдоль  контура прямоугольника. С учетом последующего перехода к пределу   она равна

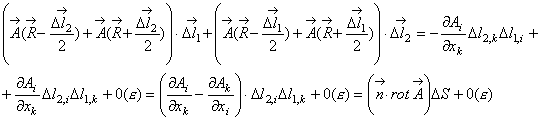 (2.41)

, где    означает бесконечно малую более высокого порядка, чем   .

Разделим правую и левую части (2.41) на      и перейдем к пределу. Тогда с учетом того, что в левой части стоит выражение для циркуляции     вдоль бесконечно малого контура, получим

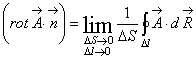        (2.42)

Проекция    на направление     равна пределу отношения циркуляции вектора      вдоль замкнутого контура, проведенного в плоскости, перпендикулярной  , к площади, ограни­ченной этим контуром, при стягивании его к точке. Рассмотрим теперь всю совокупность элементарных площадок, на которые с помощью прямоугольников, подобных только что рассмотренному, можно разбить поверхность S. Применим к каждой из них соотношение (2.41), просуммируем и перейдем к пределам, как это было сделано при выводе (2.42). Сумма правых частей приведет нас к потоку    через поверхность S. Сумма левых частей сведется к циркуляции векторного поля    по контуру L, так как общие части границ соседних элементарных площадок проходятся в противоположном направлении и при суммировании циркуляции их вклады компенсируют друг друга. Из сказанного следует

ТЕОРЕМА. Поток вихря    через поверхность S,.натянутую на замкнутый контур L , равен циркуляции векторного поля     по этому контуру, если компоненты поля вместе с их частными произ­водными непрерывны на S  и L.

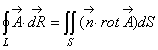          (2.43)