
- •Предмет физики. Предмет механики. Физические модели. Материальная точка. Абсолютно твердое тело. Системы отсчета.
- •Координатное и векторное описание положения частицы. Связь между ними
- •Скорость и ускорение материальной точки.
- •Равнопеременное движение.
- •Нормальное, тангенциальное и полное ускорения. Радиус кривизны траектории.
- •Поступательное и вращательное движение. Кинематика поступательного движения. Связь угловых и линейных характеристик движения.
- •Плоское движение
- •Механический принцип относительности. Инерциальные системы отсчета. Первый закон Ньютона.
- •Преобразования Галилея. Закон сложения скоростей Галилея.
- •Второй закон Ньютона. Сила. Импульс.
- •11.Принцип суперпозиции сил. Третий закон Ньютона.
- •12. Силы инерции. Принцип эквивалентности.
- •Измерения. Системы единиц. Внесистемные единицы. Размерности физических величин.
- •Работа и энергия. Мощность.
- •Консервативные силы. Потенциальные поля.
- •Потенциальная энергия. Связь силы и потенциальной энергии.
- •Силы в механике. Упругая сила.
- •Сила гравитационного притяжения. Однородная сила тяжести.
- •Сухое трение. Вязкое трение.
- •Закон сохранения механической энергии. Границы одномерного движения.
- •Закон сохранения импульса и его связь с однородностью пространства.
- •Абсолютно неупругий удар.
- •Абсолютно упругий удар.
- •Момент импульса и закон его сохранения.
- •Связь закона сохранения момента импульса с изотропностью пространства.
- •Кинетическая энергия вращающегося тела. Расчет момента инерции полого цилиндра.
- •Теорема Штейнера.
- •Динамика вращательного движения системы материальных точек относительно неподвижной оси.
- •Кинетическая энергия плоского движение твердого тела.
- •Равнодействующая сила. Центр тяжести.
- •Лоренцево замедление времени.
- •Лоренцево сокращение длин.
- •Преобразования Лоренца
- •Интервал и его инвариантность.
- •Релятивистский импульс. Основное уравнение релятивисткой динамики.
- •Кинетическая энергия релятивистской частицы. Взаимосвязь массы и энергии. Энергия покоя.
- •2 Тема.
- •1. Потенциальная энергия взаимодействия молекул. Модель идеального газа.
- •2. Жидкость. Кристаллическая решетка.
- •3. Молярная масса и число Авогадро.
- •4. Статистические ансамбли. Средние значения и среднеквадратичные отклонения.
- •6. Идеальный газ. Давление идеального газа.
- •8. Изопроцессы в идеальном газе.
- •9. Закон равнораспределения энергии по степеням свободы молекул в газе.
- •10. Внутренняя энергия. Внутренняя энергия идеального газа.
- •11. Механическая работа в тепловых процессах.
- •12. Первое начало термодинамики
- •1 3. Круговые процессы и тепловые двигатели. К.П.Д. Теплового двигателя.
- •14. Теплоемкость. Теплоемкость при постоянном давлении и теплоемкость при постоянном объеме. Уравнение Майера.
- •15. Работа в адиабатном процессе
- •16. Уравнение Пуассона.
- •17. Энтропия и ее статистический смысл.
- •18. Энтропия идеального газа.
- •19. Изменение энтропии в квазиравновесных процессах.
- •20. К.П.Д. Идеального цикла Карно.
- •21. Второе начало термодинамики (закон возрастания энтропии). Теорема Нернста.
- •22.Распределение Больцмана частиц в потенциальном поле.
- •23. Барометрическая формула.
- •24. Распределение Максвелла по скоростям.
- •25. Распределение Максвелла по модулю скорости.
- •26.Опыт Штерна.
- •27. Явления переноса. Опытные законы диффузии, теплопроводности и внутреннего трения.
- •28. Средняя длина свободного пробега молекулы в газе
- •29.Коэффициент диффузии в газе.
- •30. Коэффициент теплопроводности газов
- •31.Напряженность магнитного поля. Диамагнетики и парамагнетики.
- •32.Условия на границе раздела магнетиков.
- •33.Ферромагнетики.
- •34.Закон электромагнитной индукции. Правило Ленца.
- •35. Взаимная индукция. Самоиндукция.
- •36. Ток замыкания цепи
- •37.Ток размыкания цепи.
- •38.Физический смысл интегральной формы уравнений Максвелла.
- •39.Ток смещения.
- •40. Скорость электромагнитной волны.
- •41.Капиллярные явления.
- •42. Влияние поверхностных эффектов на конденсацию пара и испарение жидкости.
- •43. Ламинарное и турбулентное течение. Линии и трубки тока. Уравнение непрерывности.
- •44. Уравнение Бернулли.
- •46. Число Рейнольдса. Метод подобия.
- •47Деформация твердых тел. Закон Гука. Модуль Юнга.
- •1. Закон Кулона. Электрическое поле. Принцип суперпозиции.
- •3. Теорема Остроградского-Гаусса для напряженности электростатического поля.
- •4. Теорема Ирншоу.
- •5. Полярные и неполярные диэлектрики. Электрический диполь. Дипольный момент.
- •6. Вектор поляризации. Его связь с поверхностной плотностью связанных зарядов.
- •7. Поле бесконечной равномерно заряженной плоскости. Напряженность поля в диэлектрике. Относительная диэлектрическая проницаемость.
- •8. Электрическая индукция. Теорема Остроградского-Гаусса для электрической индукции. Поведение нормальной составляющей поля на границе раздела диэлектриков.
- •9. Поле бесконечной равномерно заряженной нити.
- •10. Поле равномерно заряженного шара.
- •11. Потенциал электростатического поля. Его связь с напряженностью. Поведение тангенциальных составляющих поля на границе раздела диэлектриков
- •12. Потенциал поля точечного заряда и поля электрического диполя.
- •Проводник в электрическом поле. Связь между поверхностной плотностью заряда и полем вблизи поверхности.
- •Электроемкость проводника. Электроемкость конденсатора.
- •Потенциальная энергия системы зарядов. Энергия конденсатора. Плотность энергии электрического поля.
- •16. Электрический ток - упорядоченное движение заряженных частиц под действием сил электрического поля или сторонних сил.
- •17. Законы Ома.
- •18. Закон Ома для замкнутой цепи. Правила Кирхгофа.
- •19. Мощность электрического тока это работа, совершаемая током за единицу времени.
- •20. Квазистационарные токи. Заряд и разряд конденсатора.
- •Сила Лоренца. Магнитное поле. Относительный характер электрических и магнитных компонент электромагнитного поля.
- •22.Принцип супер¬позиции магнитных полей.
- •23.Закон Био-Савара-Лапласа. Магнитное поле кругового витка на его оси.
- •24.Магнитное поле бесконечного прямолинейного проводника с током
- •25.Теорема Остроградского-Гаусса для магнитного поля. Соленоидальный характер магнитного поля. Закон полного тока.
- •26.Поле соленоида.
- •27. Закон Ампера. Сила Ампера.
- •28.Работа по перемещению проводника с током в магнитном поле
- •29.Замкнутый контур в магнитном поле.
- •30 Энергия магнитного поля соленоида. Плотность энергии магнитного поля
- •31.Напряженность магнитного поля. Диамагнетики и парамагнетики.
- •32 Условия на границе раздела магнетиков.
- •33 Феромагнетики
- •34 Закон электромагнитной индукции. Правило Ленца.
- •35.Взаимная индукция. Самоиндукция.
- •Ток замыкания цепи.
- •Ток размыкания цепи.
- •Физический смысл интегральной формы уравнений Максвелла.
- •Ток смещения.
- •Скорость электромагнитной волны.
- •Поток вектора через бесконечно малую поверхность.
- •Циркуляция вектора по бесконечно малому контуру.
- •Уравнения Максвелла в дифференциальной форме.
9. Закон равнораспределения энергии по степеням свободы молекул в газе.
Число степеней свободы – это число независимых переменных полностью определяющее положение объектов в пространстве.
1.Одноатомный газ: i поступ=3, i вращ=0, i=iпоступ+iвращ=3
2.Двухатомный газ: i поступ=3, i вращ=2, i=iпоступ+iвращ=3
Изменяет свое положение, массы молекул находятся далеко от центра, значит момент вращения относительно оси х большой и таким вращением пренебречь нельзя.
3.Трехатомный газ: i поступ=3, i вращ=3, i=iпоступ+iвращ=6
На одну степень свободы молекулы газа, приходится одинаковая энергия, равная Еo=kT\2
E mo=1\2*rT энерг одной молекулы.
10. Внутренняя энергия. Внутренняя энергия идеального газа.
Внутренняя энергия представляет собой сумму всех молекул вещества, она не зависит от движения вещества в целом и от потенциальной энергии вещества во внешнем силовом поле.
Внутренняя энергия u=(cумма отN до i=1) Еmo
Твердое тело uтт=uк(энер движ=0)+uп(элек взамодейств)=uп
Внеш энер жидкости uж=uк+uп
Жидкости весьма текучи, это доказывает что кинетическая энергия слишком велика. Жидкости практически не сжигаемы, следовательно потенциальная энергия молекул велика.
11. Механическая работа в тепловых процессах.
Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами. Как следует из первого закона термодинамики, полученное газом количество теплоты Q полностью превращается в работу A при изотермическом процессе, при котором внутренняя энергия остается неизменной (ΔU = 0): A = Q.
Но такой однократный акт преобразования теплоты в работу не представляет интереса для техники. Реально существующие тепловые двигатели (паровые машины, двигатели внутреннего сгорания и т. д.) работают циклически. Процесс теплопередачи и преобразования полученного количества теплоты в работу периодически повторяется. Для этого рабочее тело должно совершать круговой процесс или термодинамический цикл, при котором периодически восстанавливается исходное состояние.
Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q1 > 0 и отдает холодильнику количество теплоты Q2 < 0. Полное количество теплоты Q, полученное рабочим телом за цикл, равно Q = Q1 + Q2 = Q1 – |Q2|.
При обходе цикла рабочее тело возвращается в первоначальное состояние, следовательно, изменение его внутренней энергии равно нулю (ΔU = 0). Согласно первому закону термодинамики,ΔU = Q – A = 0.
Отсюда следует: A = Q = Q1 – |Q2|.
Работа
A,
совершаемая рабочим телом за цикл, равна
полученному за цикл количеству теплоты
Q.
Отношение работы A
к количеству теплоты Q1,
полученному рабочим телом за цикл от
нагревателя, называется коэффициентом
полезного действия η
тепловой машины:
![]()
Коэффициент полезного действия указывает, какая часть тепловой энергии, полученной рабочим телом от «горячего» теплового резервуара, превратилась в полезную работу. Остальная часть (1 – η) была «бесполезно» передана холодильнику. Коэффициент полезного действия тепловой машины всегда меньше единицы (η < 1). Энергетическая схема тепловой машины изображена на рис . Рисунок 3.11.2. Энергетическая схема тепловой машины: 1 – нагреватель; 2 – холодильник; 3 – рабочее тело, совершающее круговой процесс. Q1 > 0, A > 0, Q2 < 0; T1 > T2.
 .
Рисунок
3.11.2.
.
Рисунок
3.11.2.
В 1824 году французский инженер С. Карно рассмотрел круговой процесс, состоящий из двух изотерм и двух адиабат. Этот круговой процесс сыграл важную роль в развитии учения о тепловых процессах. Он называется циклом Карно (рис. 3.11.4).
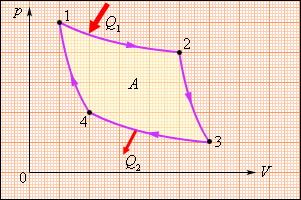
Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (1–2) газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру T1. Газ изотермически расширяется, совершая работу A12, при этом к газу подводится некоторое количество теплоты Q1 = A12. Далее на адиабатическом участке (2–3) газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу A23 > 0. Температура газа при адиабатическом расширении падает до значения T2. На следующем изотермическом участке (3–4) газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре T2 < T1. Происходит процесс изотермического сжатия. Газ совершает работу A34 < 0 и отдает тепло Q2 < 0, равное произведенной работе A34. Внутренняя энергия газа не изменяется. Наконец, на последнем участке адиабатического сжатия газ вновь помещается в адиабатическую оболочку. При сжатии температура газа повышается до значения T1, газ совершает работу A41 < 0. Полная работа A, совершаемая газом за цикл, равна сумме работ на отдельных участках:A = A12 + A23 + A34 + A41.
На диаграмме (p, V) эта работа равна площади цикла. Как следует из первого закона термодинамики, работа газа при адиабатическом расширении (или сжатии) равна убыли ΔU его внутренней энергии. Для 1 моля газаA = –ΔU = –CV(T2 – T1),
где T1 и T2 – начальная и конечная температуры газа. Отсюда следует, что работы, совершенные газом на двух адиабатических участках цикла Карно, одинаковы по модулю и противоположны по знакамA23 = –A41.
По определению, коэффициент полезного действия η цикла Карно есть
![]()
Карно
выразил коэффициент полезного действия
цикла через температуры нагревателя
T1
и холодильника T2:
![]()
