30 Энергия магнитного поля соленоида. Плотность энергии магнитного поля

Проводник, c протекающим по нему электрическим ток, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля.

Рассмотрим контур индуктивностью L, по которому протекает ток I. С этим контуром сцеплен магнитный поток Ф=LI, поскольку индуктивность контура неизменна, то при изменении тока на dI магнитный поток изменяется на dФ=LdI. Но для изменения магнитного потока на величину dФ следует совершить работу dА=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф равна

Значит, энергия магнитного поля, которое связано с контуром,

(1)

Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (1) формулу индуктивности соленоида, найдем

Так как I=Bl/(μ0μN) и В=μ0μH , то

(2)

где Sl = V — объем соленоида.

Магнитное поле внутри соленоида однородно и сосредоточено внутри него, поэтому энергия (2) заключена в объеме соленоида и имеет с нем однородное распределение с постоянной объемной плотностью

(3)

Формула (3) для объемной плотности энергии магнитного поля имеет вид, аналогичный выражению для объемной плотности энергии электростатического поля, с тем отличием, что электрические величины заменены в нем магнитными. Формула (3) выводилась для однородного поля, но она верна и для неоднородных полей. Формула (3) справедлива только для сред, для которых линейная зависимость В от Н , т.е. оно относится только к пара- и диамагнетикам.

Плотность энергии магнитного поля в соленоиде с сердечником будет складываться из энергии поля в вакууме и в магнетике сердечника:

, отсюда

Т.к. в вакууме , имеем

31.Напряженность магнитного поля. Диамагнетики и парамагнетики.

Напряженность магнитного поля [H] – это отношение магнитной индукции к магнитной проницаемости среды

Напряженность магнитного поля – величина векторная. За единицу измерения напряженности магнитного поля в Международной системе единиц принят ампер на метр.

Если в бесконечно длинном прямолинейном проводе ничтожно малого кругового сечения, помещенном в однородную среду, протекает ток в 2π ампера, то в точках магнитного поля, удаленных от оси провода на расстояние 1 метра, напряженность магнитного поля равна 1 а/м.

Рассмотрим, как определяется направление магнитного поля для случая прямолинейного проводника и кольцевого тока.

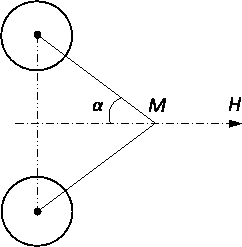
Напряжение магнитного поля прямолинейного проводника с током определяет правило правого винта: если винт ввинчивается так, чтобы он поступательно перемещался по направлению тока, то направление вращения его головки будет совпадать с направлением магнитных силовых линий.

Напряженность магнитного поля в какой-либо точке оси МН кольцевого тока определяется по формуле

где I – ток в амперах;

R – радиус кольца в метрах;

α – угол, составленный осью кольца и прямой линией, проведенной к средней линии кольца из данной точки.

В центре кольца на его оси, где α = 90, напряженность магнитного поля определяется по формуле

Направление магнитного поля внутри кольца определяется правилом буравчика: если вращательное движение буравчика совпадает с направлением тока в кольце, то поступательное движение буравчика совпадает с направлением магнитного поля внутри кольца.

Напряженность магнитного поля внутри соленоида большой длины в точках на его оси определяется по формуле

где W – число витков соленоида;

l – длина соленоида в метрах;

I – ток в амперах.

Неаправление магнитного поля внутри соленоида определяется по правилу правой руки:если правую руку положить на соленоид так, чтобы четыре вытянутых пальца совпадали с направлением тока в нем, то отставленный большой палец покажет направление выхода магнитных силовых линий. Магнитные силовые линии выходят из северного полюса и замыкаются на южном.

Вещества, способные намагничиваться во внешнем магнитном поле, т. е. создавать собственное (внутреннее) магнитное поле самого вещества называются магнетиками. По своим магнитным свойствам магнетики подразделяются на слабомагнитные и сильномагнитные вещества. К слабомагнитным веществам относятся парамагнетики и диамагнетики. Основную группу сильномагнитных веществ составляют ферромагнетики. Слабо- и сильномагнитные вещества отличаются величиной относительной магнитной проницаемости μ. Для слабомагнитных веществ μ незначительно отличается от единицы: для парамагнетиков μ≥1, для диамагнетиков μ≤1. Кроме того, μ для слабомагнитных веществ не зависит от индукции того магнитного поля, в котором намагничиваются вещества. Для сильномагнитных веществ μ>>1 и зависит от .

К парамагнетикам относятся кислород, окись азота, алюминий, платина, редкоземельные элементы, щелочные и щелочноземельные металлы и другие вещества. Парамагнетики намагничиваются во внешнем магнитном поле по направлению этого поля, т.е. внутреннее поле парамагнетика сонаправлено с внешним полем ( ↑↑ ) Для парамагнитных веществ μ зависит от температуры и убывает с повышением ее по закону:

(4.13)

где Т — термодинамическая температура, С — постоянная Кюри, характерная для данного вещества.

Диамагнетиками являются инертные газы (гелий, аргон и др.), многие металлы (золото, цинк, медь, ртуть, серебро), вода, стекло, мрамор, многие органические соединения. Диамагнетики намагничиваются во внешнем магнитном поле против направления этого поля, т.е. ↑↓ . Для этих веществ относительная магнитная проницаемость не зависит от температуры.

Пара- и диамагнетики в отсутствие внешнего магнитного поля не способны намагничиваться, т.е. в них не возникает внутреннее магнитное поле.

К ферромагнетикам относится сравнительно небольшая группа твердых кристаллических тел — так называемых переходных металлов (железо, никель, кобальт), а также ряд сплавов. Ферромагнетики – это вещества, обладающие спонтанной намагниченностью, т.е. они обладают внутренним полем при отсутствии внешнего магнитного поля. Относительная магнитная проницаемость μ ферромагнетиков, в отличие от пара- и диамагнетиков, имеет весьма большие значения.