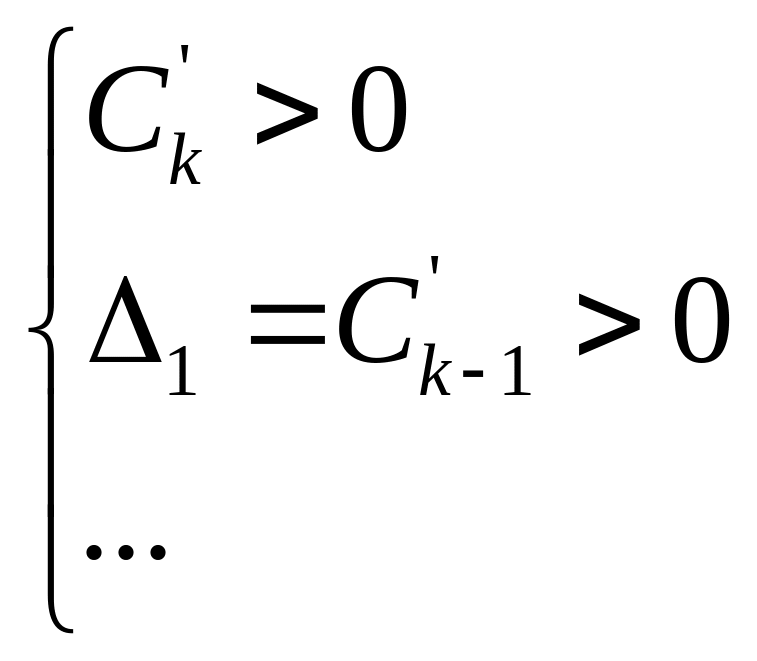Математическое описание дискретных процессов.

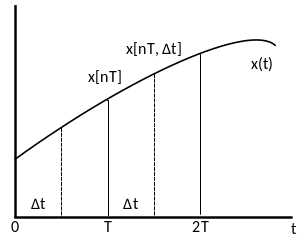
Дискретные функции определены только для дискретного аргумента и при фиксированном интервале между отсчетамиТназываются решетчатыми функциями.

Решетчатая функция:

Для описания значений процессов , сдвинутых относительно момента времени nT на интервал ∆t используется смещенная решетчатая функция:

Смещенная решетчатая функция используется для описания непрерывных процессов, если считать ∆t непрерывно изменяющимся в интервале (0;Т).

Для унификации анализа систем решетчатые функции нормируются по времени, путем введения относительного времени:

Нормированная решетчатая функция:

где Ɛ – относительное смещение:

Для решетчатых функций существуют понятия, аналогичные понятиям для непрерывных функций. Например, эквивалентом производной для непрерывной функции является разность.

Аналогично вводятся разности более высоких порядков. Например, 2-го порядка:

3-го порядка:

Разность любого порядка можно записать через значения решетчатой функции:

Для решетчатой функции аналогом дифференциального уравнения является разностное уравнение. Разностное уравнение можно записать в 2 формах:

1. каноническая форма:

2. рекуррентная форма:

По разностному уравнению можно записать передаточную функцию системы, взяв разностное уравнение дискретного преобразования Лапласа (ДПЛ). ДПЛ существует в 2 формах:

1. В форме D-преобразования.

2. В форме Z-преобразования.

D-преобразование функции x[n]:

Z-преобразование функции x[n]:

Найдем Z-преобразование решетчатой функции , сдвинутой на целое число периодов, если:

При нулевых начальных условиях получается:

Возьмем дискретное преобразование от разностного уравнения в рекуррентной форме:

Передаточная функция:

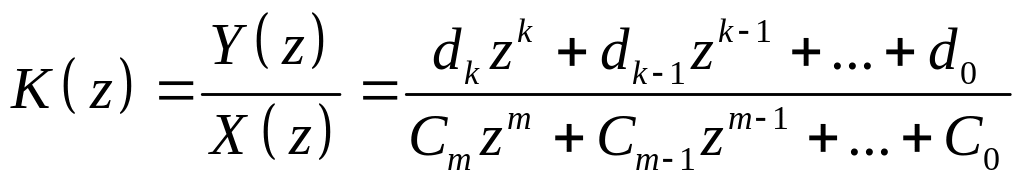
Устойчивость дискретных систем.

Считаем, что система устойчива, если при ограниченном входном воздействии выходной процесс тоже ограничен. Используем прямой метод оценки устойчивости, решая разностное уравнение.

Решение:

При ограниченном входном воздействии принужденная составляющая тоже будет ограниченной, т.к. она определяется тоже этим воздействием, значит, неограниченной может быть только свободная составляющая, которая является решением однородного дифференциального уравнения.

Решение этого уравнения записывается в виде суммы дискретных экспонент.

Непрерывная экспонента:

Дискретная экспонента:

где z_i – корни характеристического уравнения:

Система устойчива, если:

_{Ai – не могут быть ∞ и нулевыми, поэтому:}

Дискретная система устойчива, если все корни характеристического уравнения находятся внутри окружности единичного радиуса.

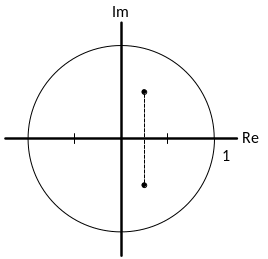
Для определения устойчивости систем обычно пользуются не этим условием, а критериями устойчивости. Эти критерии называются также как и для непрерывных систем.

Критерий устойчивости Гурвица.

Критерий Гурвица, сформулированный для непрерывных систем, определяет требования к коэффициентам характеристического уравнения, при выполнении которых корни будут находиться в левой полуплоскости. Нам же нужно определить требования, при которых корни характеристического уравнения будут находиться внутри окружности единичного радиуса.

Для отображения внутренности окружности в левую полуплоскость используется билинейное преобразование:

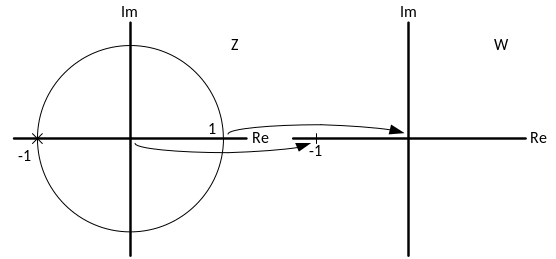
Сначала нужно характеристическое уравнение преобразовать к другой переменной.

Для определения устойчивости составляется матрица Гурвица:

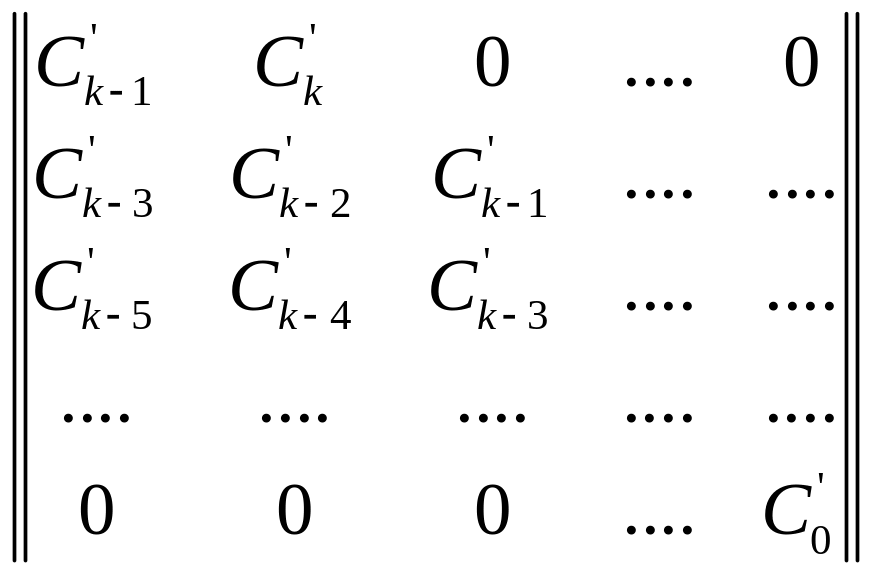
Дискретная система устойчива, если при С_К’>0 все определители Гурвица положительны.