Бесконечно большие величины
Определение.
Функция
называется бесконечно большой при
,
если ее предел равен бесконечности:
.
Свойства бесконечно больших величин
Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.
Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.
Частное от деления бесконечно большой величины на функцию, имеющую предел, есть величина бесконечно большая.
Об отношении или
разности двух бесконечно больших функций
никакого общего заключения сделать
нельзя. В этих случаях говорят о
неопределенностях вида
или
.
В зависимости от характера изменения
бесконечно больших величин их отношение
или разность может оказаться или числом,
или бесконечно малой, или бесконечно
большой.
Связь между бесконечно малыми и бесконечно большими величинами
Теорема.
Если функция
есть бесконечно малая величина при
(
),
то функция
является бесконечно
большой
при
(
).
И, наоборот, если функция
бесконечно большая при
(
),
то функция
есть величина бесконечно малая при
(
).
19. Второй замечательный предел, число е. Понятие о натуральных логарифмах. Второй замечательный предел.
Определение.
Числом
(вторым замечательным пределом) называется
предел числовой последовательности
:
,
где
Прямым
вычислением можно убедиться, что
,
(иррациональное число, число Эйлера).
Если рассмотреть
функцию
,
то при
функция имеет предел, равный числу
:
.
Или если
,
то
.
Непосредственное
вычисление этого предела приводит к
неопределенности
.
Однако доказано, что он равен числу
.
Второй замечательный предел необходимо
всегда использовать при раскрытии
неопределенности вида
.
Число
(число Эйлера, неперово число) играет
важную роль в математическом анализе.
График функции
Рассмотрим примеры
вычисления пределов. Получил название
экспоненты. Широко используются логарифмы
по основанию
,
называемые натуральными. Натуральные
логарифмы обозначаются символом
.
Пример.
.
Пример.
=
.
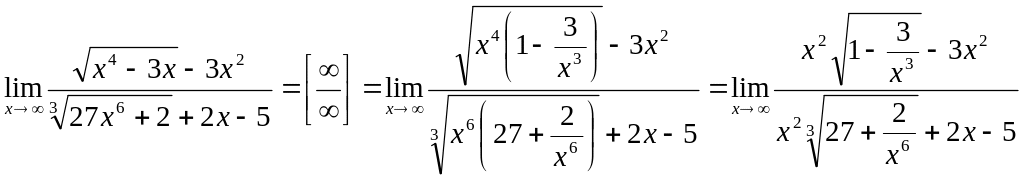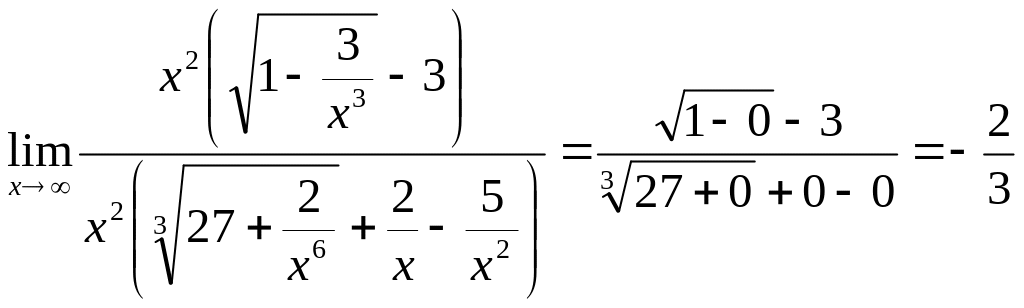Пример.
.
Пример.
.
Пример.
.
Пример.
.
Пример.
.
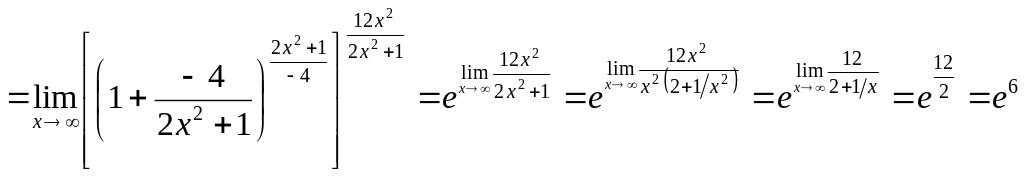20. Непрерывность функции в точке и на промежутке. Свойства функций, непрерывных на отрезке. Точки разрыва. Примеры. Непрерывность функции
Определение 1. Функция называется непрерывной в точке , если она удовлетворяет следующим условиям:
1) определена в
точке
,
т.е. существует
;
2) имеет конечные односторонние пределы функции при слева и справа;
3) эти пределы равны значению функции в точке , т.е.
.
Пример.
Исследовать
функции на непрерывность в точке
:
а)
,
б)
.
Решение.
а)
.
При
функция определена,
,
,
,
т.е. все три условия непрерывности
функции в точке выполнены. Следовательно,
функция
в точке
непрерывна.
б)
.
При
функция не определена;
;
.
Т.о. в точке функция не является непрерывной, т.к. не выполнены первое и третье условия непрерывности функции в точке.
Определение
2. Функция
называется непрерывной в точке
,
если она определена в этой точке и
бесконечно малому приращению аргумента
соответствует бесконечно малое приращение
функции:
.
Определения 1 и 2 равносильны.
Точка называется точкой разрыва функции , если эта функция в данной точке не является непрерывной. Различают точки разрыва:
Первого рода – когда существуют конечные односторонние пределы функции слева и справа при , не равные друг другу. К точкам разрыва первого рода относятся также точки устранимого разрыва, когда предел функции при существует, но не равен значению функции в этой точке.
Второго рода – когда хотя бы один из односторонних пределов слева или справа равен бесконечности или не существует.