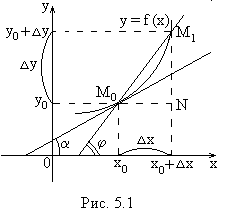- •Метод обратной матрицы.
- •11. Теорема и формулы Крамера решения системы п линейных уравнений с п переменными (без вывода).
- •Решение системы линейных уравнений с неизвестными
- •12. Понятие функции, способы задания функций. Область определения. Четные и нечетные, ограниченные, монотонные функции. Примеры. Понятие функции одной переменной
- •Способы задания функций:
- •Основные свойства функций
- •13. Понятие элементарной функции. Основные элементарные функции и их графики (постоянная, степенная, показательная, логарифмическая). Элементарная функция
- •Основные элементарные функции
- •14. Уравнение линии на плоскости. Точка пересечения двух линий. Основные виды уравнений прямой на плоскости (одно из них вывести). Уравнение линии на плоскости
- •Взаимное расположение двух линий
- •Уравнение прямой на плоскости
- •Уравнение прямой, проходящей через заданную точку в данном направлении
- •Уравнение пучка прямых Уравнение прямой в отрезках
- •Общее уравнение прямой и его исследование
- •Точка пересечения прямых
- •15. Общее уравнение прямой на плоскости, его исследование. Условия параллельности и перпендикулярности прямых. Общее уравнение прямой и его исследование
- •Условия параллельности и перпендикулярности двух прямых:
- •16. Предел последовательности при и предел функции при . Признаки существования предела (с доказательством теоремы о пределе промежуточной функции). Предел числовой последовательности
- •Предел функции в бесконечности и в точке
- •Признаки существования предела
- •17. Определение предела функции в точке. Основные теоремы о пределах (одну из них доказать). Предел функции в точке
- •Основные теоремы о пределах. Признаки существования предела
- •Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.Е.
- •Предел произведения конечного числа функций равен произведению пределов этих функций, т.Е.
- •Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.Е.
- •Бесконечно большие величины
- •Свойства бесконечно больших величин
- •Связь между бесконечно малыми и бесконечно большими величинами
- •19. Второй замечательный предел, число е. Понятие о натуральных логарифмах. Второй замечательный предел.
- •20. Непрерывность функции в точке и на промежутке. Свойства функций, непрерывных на отрезке. Точки разрыва. Примеры. Непрерывность функции
- •Свойства функций, непрерывных в точке
- •1. Если функции и непрерывны в точке , то их сумма , произведение и частное (при условии ) являются функциями, непрерывными в точке .
- •2. Если функция непрерывна в точке и , то существует такая окрестность точки , в которой .
- •Точки разрыва функции
- •Свойства функций, непрерывных на отрезке
- •21. Производная и ее геометрический смысл. Уравнение касательной к плоской кривой в заданной точке. Определение производной
- •Задача о касательной
- •22. Дифференцируемость функций одной переменной. Связь между дифференцируемостью и непрерывностью функции (доказать теорему). Понятие дифференцируемости функции
- •Связь между дифференцируемостью функции и ее непрерывностью
- •23. Основные правила дифференцирования функций одной переменной (одно из этих правил доказать).
- •Основные правила дифференцирования
- •Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных этих функций, т.Е.
- •5. Производная частного двух дифференцируемых функций может быть найдена по формуле
- •24. Формулы производных основных элементарных функций (одну из формул вывести). Производная сложной функции. Производные основных элементарных функций (таблица производных)
- •Производная сложной функции
- •25. Теоремы Ролля и Лагранжа (без доказательства). Геометрическая интерпретация этих теорем.
- •27. Определение экстремума функции одной переменной. Необходимый признак экстремума (доказать).
- •29. Понятие асимптоты графика функции. Горизонтальные, наклонные и вертикальные асимтоты. Примеры.
- •30. Общая схема исследования функций и построения их графиков. Пример.
- •31. Функции нескольких переменных. Примеры. Частные производные (определение). Экстремум функции нескольких переменных и его необходимые условия. Основные понятия. Частные производные
- •Частные производные функции двух переменных
- •Экстремум функции двух переменных
- •35. Метод замены переменной в неопределенном интеграле и особенности применения этого метода при вычислении определенного интеграла.
- •36. Метод интегрирования по частям для случаев неопределенного и определенного интегралов (вывести формулу). Примеры.
- •Методы вычисления определенного интеграла
- •37. Определенный интеграл как предел интегральной суммы. Свойства определенного интеграла.
- •Геометрический смысл определенного интеграла.
- •Экономический смысл определенного интеграла.
- •Свойства определенного интеграла
- •38. Теорема о производной определенного интеграла по переменному верхнему пределу. Формула Ньютона—Лейбница. Определенный интеграл с переменным верхним пределом
- •Формула Ньютона-Лейбница.
- •40. Вычисление площадей плоских фигур с помощью определенного интеграла. Примеры.
- •41. Понятие о дифференциальном уравнении. Общее и частное решения. Задача Коши. Задача о построении математической модели демографического процесса.
- •Задача о построении математической модели демографического процесса. Задача Коши
- •42. Простейшие дифференциальные уравнения 1-го порядка (разрешенные относительно производной, с разделяющимися переменными) и их решение. Примеры.
- •Рассмотрим некоторые типы дифференциальных уравнений 1-го порядка.
- •Неполные дифференциальные уравнения 1-порядка.
- •Дифференциальные уравнения 1-го порядка с разделяющимися переменными.
Задача о касательной
Пусть на плоскости
![]() дана непрерывная функция
и необходимо найти уравнение касательной
к этой кривой в точке
дана непрерывная функция
и необходимо найти уравнение касательной
к этой кривой в точке
![]() .
.
|
Уравнение прямой
по точке
где
Из
Если точку
приближать к точке
при
Следовательно,
|
Из задачи о касательной следует геометрический смысл производной: производная f′(x0) есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой у=f′(x) в точке х0, т.е. k= f′(x0).
Следовательно, уравнение касательной к кривой y=f(x) в точке х0 примет вид
![]()
Пример. Найти производную функции f(x)=х2.
Решение. Придавая аргументу х приращение ∆х, найдем соответствующее приращение функции:
![]()
Составим отношение:
![]()
Найдем предел этого отношения при ∆х → 0:
![]()
22. Дифференцируемость функций одной переменной. Связь между дифференцируемостью и непрерывностью функции (доказать теорему). Понятие дифференцируемости функции
Определение. Функция y=f(x) называется дифференцируемой в точке х, если ее приращение Δу в этой точке можно представить в виде
![]() ,
,
где А – некоторое число, не зависящее
от
![]() ,
а α(
)
– функция аргумента
,
являющаяся бесконечно малой при
→0,
т.е.
,
а α(
)
– функция аргумента
,
являющаяся бесконечно малой при
→0,
т.е.
![]()
Выясним теперь связь между дифференцируемостью в точке и существованием производной в той же точке.
Теорема. Для того чтобы функция f(x) была дифференцируемой в данной точке х , необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Связь между дифференцируемостью функции и ее непрерывностью
Пример. Доказать, что функция y=│х│ недифференцируема в точке х=0 .
Решение. Производная функции (если она существует) равна
![]()
Очевидно, что при х=0 производная
не существует, так как отношение
![]() ,
т.е. не имеет предела при Δх→0 (ни
конечного, ни бесконечного). Геометрически
это означает отсутствие касательной
к кривой в точке х=0.
,
т.е. не имеет предела при Δх→0 (ни
конечного, ни бесконечного). Геометрически
это означает отсутствие касательной
к кривой в точке х=0.
Теорема. Если функция y=f(x) дифференцируема в точке х0,, то она в этой точке непрерывна.
□Доказательство. По условия функция y=f(x) дифференцируема в точке х0, т.е. существует конечный предел
![]()
где f′(x0) – постоянная величина, не зависящая от .
Тогда на основании теоремы о связи бесконечно малых величин с пределами функций можно записать
![]()
где α(∆х) является бесконечно малой величиной при →0, или
![]() .
.
При Δх→0 на основании свойств бесконечно малых величин устанавливаем, что Δу→0 и, следовательно, по определению непрерывности функции в точке, делаем вывод, что функция непрерывна в токе х0. ■
Обратная теорема, вообще говоря, неверна,
если функция непрерывна в данной точке,
то она не обязательно дифференцируема
в этой точке. Так, функция y=│х│
непрерывна в точке х0=0,
ибо
![]() но, как было доказано ранее недифференцируема
в этой точке.
но, как было доказано ранее недифференцируема
в этой точке.
Таким образом, непрерывность функции – необходимое, но не достаточное условие ее дифференцируемости.
Замечание: Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором промежутке Х, то функция называется гладкой на этом промежутке. Если же производная функция допускает конечное число точек разрыва, то такая функция на данном промежутке называется кусочно гладкой.