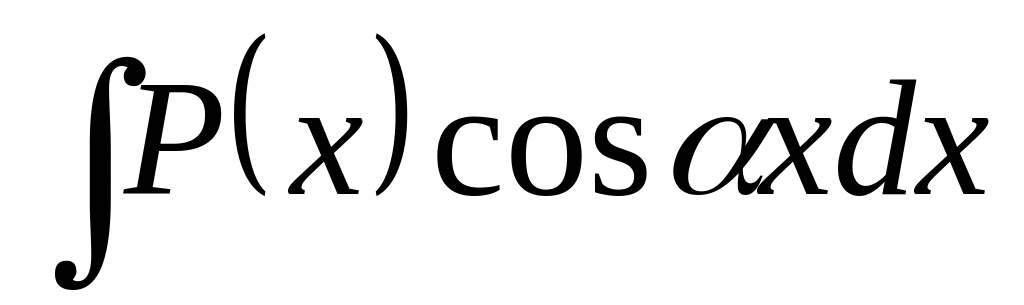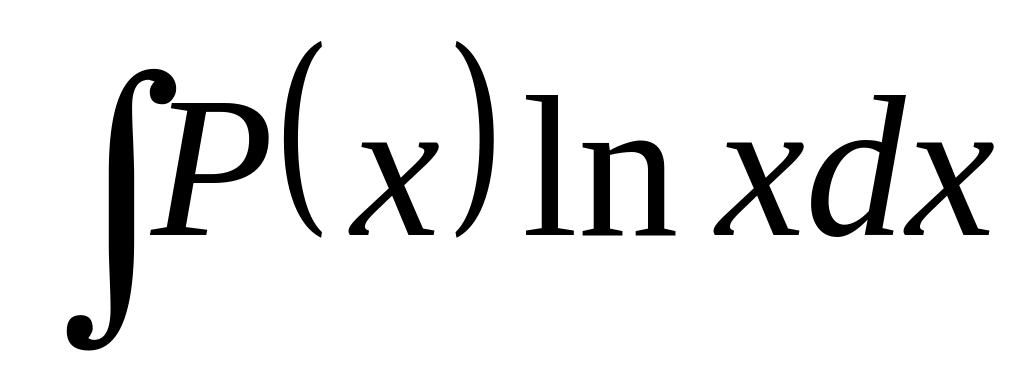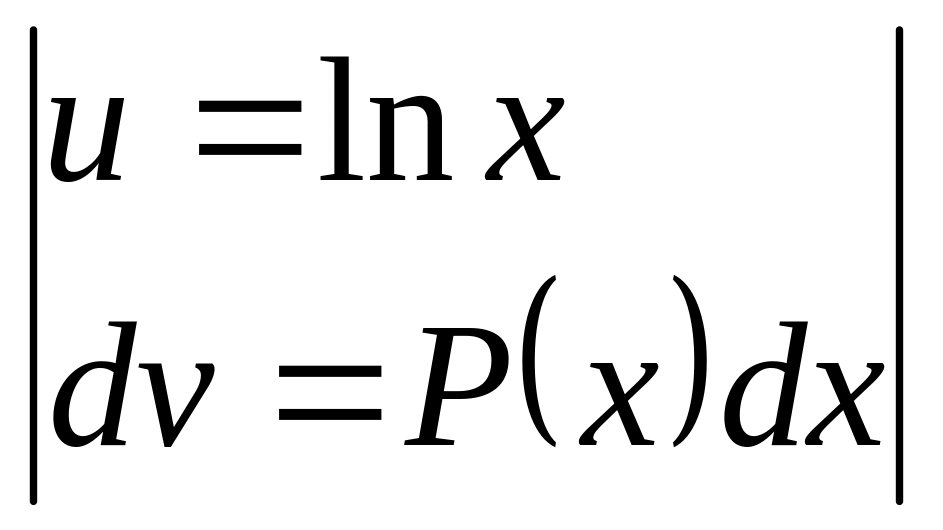- •Метод обратной матрицы.
- •11. Теорема и формулы Крамера решения системы п линейных уравнений с п переменными (без вывода).
- •Решение системы линейных уравнений с неизвестными
- •12. Понятие функции, способы задания функций. Область определения. Четные и нечетные, ограниченные, монотонные функции. Примеры. Понятие функции одной переменной
- •Способы задания функций:
- •Основные свойства функций
- •13. Понятие элементарной функции. Основные элементарные функции и их графики (постоянная, степенная, показательная, логарифмическая). Элементарная функция
- •Основные элементарные функции
- •14. Уравнение линии на плоскости. Точка пересечения двух линий. Основные виды уравнений прямой на плоскости (одно из них вывести). Уравнение линии на плоскости
- •Взаимное расположение двух линий
- •Уравнение прямой на плоскости
- •Уравнение прямой, проходящей через заданную точку в данном направлении
- •Уравнение пучка прямых Уравнение прямой в отрезках
- •Общее уравнение прямой и его исследование
- •Точка пересечения прямых
- •15. Общее уравнение прямой на плоскости, его исследование. Условия параллельности и перпендикулярности прямых. Общее уравнение прямой и его исследование
- •Условия параллельности и перпендикулярности двух прямых:
- •16. Предел последовательности при и предел функции при . Признаки существования предела (с доказательством теоремы о пределе промежуточной функции). Предел числовой последовательности
- •Предел функции в бесконечности и в точке
- •Признаки существования предела
- •17. Определение предела функции в точке. Основные теоремы о пределах (одну из них доказать). Предел функции в точке
- •Основные теоремы о пределах. Признаки существования предела
- •Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.Е.
- •Предел произведения конечного числа функций равен произведению пределов этих функций, т.Е.
- •Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.Е.
- •Бесконечно большие величины
- •Свойства бесконечно больших величин
- •Связь между бесконечно малыми и бесконечно большими величинами
- •19. Второй замечательный предел, число е. Понятие о натуральных логарифмах. Второй замечательный предел.
- •20. Непрерывность функции в точке и на промежутке. Свойства функций, непрерывных на отрезке. Точки разрыва. Примеры. Непрерывность функции
- •Свойства функций, непрерывных в точке
- •1. Если функции и непрерывны в точке , то их сумма , произведение и частное (при условии ) являются функциями, непрерывными в точке .
- •2. Если функция непрерывна в точке и , то существует такая окрестность точки , в которой .
- •Точки разрыва функции
- •Свойства функций, непрерывных на отрезке
- •21. Производная и ее геометрический смысл. Уравнение касательной к плоской кривой в заданной точке. Определение производной
- •Задача о касательной
- •22. Дифференцируемость функций одной переменной. Связь между дифференцируемостью и непрерывностью функции (доказать теорему). Понятие дифференцируемости функции
- •Связь между дифференцируемостью функции и ее непрерывностью
- •23. Основные правила дифференцирования функций одной переменной (одно из этих правил доказать).
- •Основные правила дифференцирования
- •Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных этих функций, т.Е.
- •5. Производная частного двух дифференцируемых функций может быть найдена по формуле
- •24. Формулы производных основных элементарных функций (одну из формул вывести). Производная сложной функции. Производные основных элементарных функций (таблица производных)
- •Производная сложной функции
- •25. Теоремы Ролля и Лагранжа (без доказательства). Геометрическая интерпретация этих теорем.
- •27. Определение экстремума функции одной переменной. Необходимый признак экстремума (доказать).
- •29. Понятие асимптоты графика функции. Горизонтальные, наклонные и вертикальные асимтоты. Примеры.
- •30. Общая схема исследования функций и построения их графиков. Пример.
- •31. Функции нескольких переменных. Примеры. Частные производные (определение). Экстремум функции нескольких переменных и его необходимые условия. Основные понятия. Частные производные
- •Частные производные функции двух переменных
- •Экстремум функции двух переменных
- •35. Метод замены переменной в неопределенном интеграле и особенности применения этого метода при вычислении определенного интеграла.
- •36. Метод интегрирования по частям для случаев неопределенного и определенного интегралов (вывести формулу). Примеры.
- •Методы вычисления определенного интеграла
- •37. Определенный интеграл как предел интегральной суммы. Свойства определенного интеграла.
- •Геометрический смысл определенного интеграла.
- •Экономический смысл определенного интеграла.
- •Свойства определенного интеграла
- •38. Теорема о производной определенного интеграла по переменному верхнему пределу. Формула Ньютона—Лейбница. Определенный интеграл с переменным верхним пределом
- •Формула Ньютона-Лейбница.
- •40. Вычисление площадей плоских фигур с помощью определенного интеграла. Примеры.
- •41. Понятие о дифференциальном уравнении. Общее и частное решения. Задача Коши. Задача о построении математической модели демографического процесса.
- •Задача о построении математической модели демографического процесса. Задача Коши
- •42. Простейшие дифференциальные уравнения 1-го порядка (разрешенные относительно производной, с разделяющимися переменными) и их решение. Примеры.
- •Рассмотрим некоторые типы дифференциальных уравнений 1-го порядка.
- •Неполные дифференциальные уравнения 1-порядка.
- •Дифференциальные уравнения 1-го порядка с разделяющимися переменными.
35. Метод замены переменной в неопределенном интеграле и особенности применения этого метода при вычислении определенного интеграла.
Метод замены переменной (метод подстановки).
Одним из основных методов интегрирования является метод замены переменной (или метод подстановки), описываемый формулой:
![]() (1)
(1)
Пусть
заданный интеграл
![]() не может быть непосредственно преобразован
к табличному интегралу. Введем новую
переменную
не может быть непосредственно преобразован
к табличному интегралу. Введем новую
переменную
![]() :
:
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
т.е.
.
,
т.е.
.
□ Найдем
производные по переменной
от левой и правой части;
![]() ,
,
![]() .
Т.к.
.
Т.к.
![]() ,
то эти производные равны, поэтому по
следствию Лагранжа левая и правая части
(1)
отличаются на некоторую постоянную.
Поскольку сами неопределенные интегралы
определены с точностью до неопределенного
постоянного слагаемого, то указанную
постоянную в окончательной записи можно
опустить.■
,
то эти производные равны, поэтому по
следствию Лагранжа левая и правая части
(1)
отличаются на некоторую постоянную.
Поскольку сами неопределенные интегралы
определены с точностью до неопределенного
постоянного слагаемого, то указанную
постоянную в окончательной записи можно
опустить.■
Формула показывает, что переходя к новой переменной, достаточно выполнить замену переменной в подынтегральном выражении. Удачная замена переменной позволяет упростить исходный интеграл, свести его к табличному.
Пример.
Найти
![]() .
.
Решение.
![]() .
.
Замечание. Новую переменную можно не выписывать явно, а производить преобразования функции под знаком дифференциала (путем введения постоянных и переменных под знак дифференциала).
Теорема.
Пусть
![]() некоторая первообразная для функции
некоторая первообразная для функции
![]() .
Тогда если вместо аргумента
подынтегральной функции
и первообразной
подставить выражение
.
Тогда если вместо аргумента
подынтегральной функции
и первообразной
подставить выражение
![]() ,
то это приведет к появлению дополнительного
множителя
,
то это приведет к появлению дополнительного
множителя
![]() перед первообразной:
перед первообразной:
![]() ,
где
и
,
где
и
![]() - некоторые числа,
- некоторые числа,
![]() .
.
□
Перепишем
![]() в виде:
в виде:
![]() .
Но
.
Но
![]() .
Вынося постоянный множитель
за знак интеграла и деля левую и правую
части равенства на
,
приходим к
.■
.
Вынося постоянный множитель
за знак интеграла и деля левую и правую
части равенства на
,
приходим к
.■
Алгоритм вычисления:
Делаем замену.
Дифференцируем замену
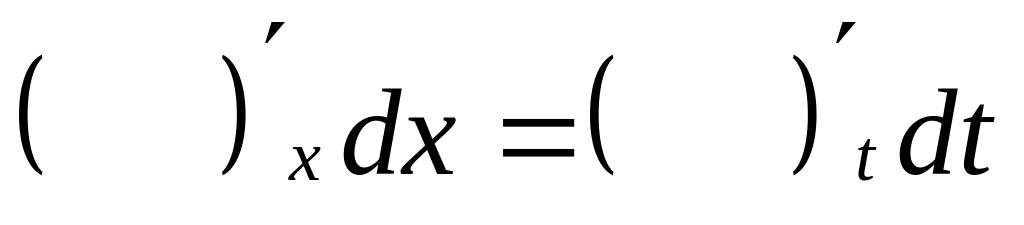 .
.Под знаком интеграла переходим к новой переменной.
Находим табличный интеграл.
Возвращаемся к старой переменной.
36. Метод интегрирования по частям для случаев неопределенного и определенного интегралов (вывести формулу). Примеры.
Интегрирование - действие, обратное дифференцированию, то каждому правилу дифференцирования должно соответствовать некоторое правило интегрирования.
Пусть
![]() и
и
![]() - дифференцируемые функции от
х.
Имеем:
- дифференцируемые функции от
х.
Имеем:
![]() ,
откуда
,
откуда
![]() .
.
Интегрируя
обе части последнего равенства, получим:
![]() ,
или
,
или
![]() .
.
Это и есть формула интегрирования по частям.
Интегрирование
по частям состоит в том, что подынтегральное
выражение
![]() представляется каким-либо образом в
виде произведения двух множителей
и
представляется каким-либо образом в
виде произведения двух множителей
и
![]() (последний обязательно содержит
(последний обязательно содержит
![]() )
и согласно формуле данное интегрирование
заменяется двумя:
)
и согласно формуле данное интегрирование
заменяется двумя:
1) при отыскании из выражения для ;
2)
при отыскании интеграла от
![]() .
.
Может оказаться, что эти два интегрирования легко осуществляются, тогда как заданный интеграл непосредственно найти трудно.
Правило интегрирования по частям нередко позволяет довести интегрирование до конца.
Пример.
Найти
![]() .
.
Решение.
![]()
Пример.
Найти
![]() .
.
Решение.
![]() .
.
Некоторые типы интегралов, берущиеся посредством формулы интегрирования по частям:
-
 ,
где
,
где
 - многочлен
- многочлен